Key points
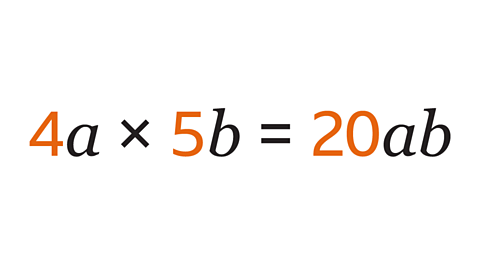
Algebraic termAn element within an algebraic sentence. Elements (terms) are separated by + or - signs. and expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms. can be multiplied.
Algebraic terms can be multiplied together and one algebraic term can be divided by another.
Two or more terms may be multiplied or divided to give a single simplified term.
To be able to multiply and divide terms correctly, it is important to have a good understanding of algebraic notationA series or system of written symbols used to represent numbers, amounts or elements in mathematics., the laws of indices and multiplication and division.
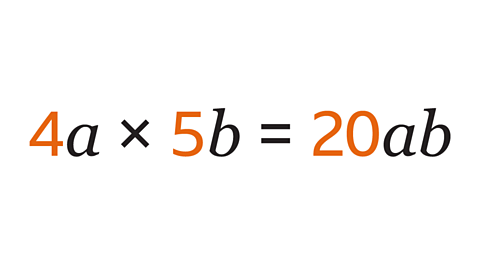
Simplifying terms by multiplying
To simplify terms using multiplication:
Multiply the constantThe number or quantity that does not vary. Eg, in the equation 𝒚 = 3𝒙 + 6, the 3 and 6 are constants, where 𝒙 and 𝒚 are variables. to find the coefficientA number or symbol multiplied with a variable or an unknown quantity in an algebraic term. Eg, 5 is the coefficient of 5𝒏 of the simplified term.
Multiply matching variableAn unknown value, usually represented by a letter like 𝒙 or 𝒚 using the laws of indices.
Different variables are written next to each other in alphabetical order.
Be sure to add indexThe index (or exponent) of a number says how many times to use the number in a multiplication. The plural of index is indices., when multiplying terms with the same baseThe number that gets multiplied when using an exponent (index). variable.
Examples
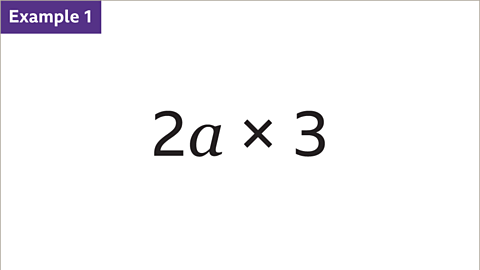
Image caption, The terms 2𝒂 and 3 are multiplied. Simplify 2𝒂 × 3
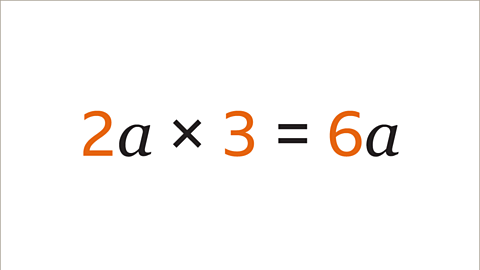
Image caption, Multiply the constants (2 and 3) to find the coefficient of the simplified term (6). Write the variable (𝒂) after the coefficient. 2𝒂 × 3 = 6𝒂

Image caption, The terms 4𝒂 and 5𝒃 are multiplied. Simplify 4𝒂 × 5𝒃

Image caption, Multiply the constants (4 and 5) to find the coefficient of the simplified term (20). Different variables (𝒂 and 𝒃) are written next to each other in alphabetical order (𝒂𝒃). The simplified term is 20𝒂𝒃
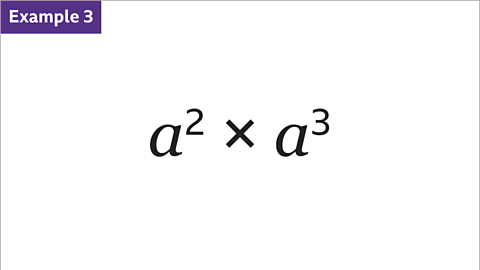
Image caption, The terms 𝒂² and 𝒂³ are multiplied. Simplify 𝒂² × 𝒂³
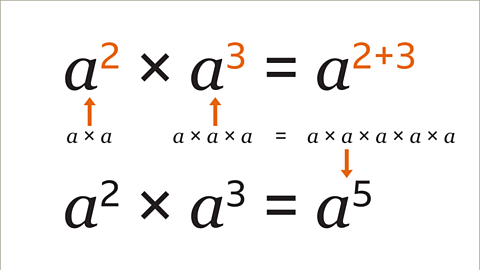
Image caption, Multiply matching variables using the laws of indices. Add the indices (2 + 3 = 5) when multiplying terms with the same base variable (𝒂). The simplified term is 𝒂⁵
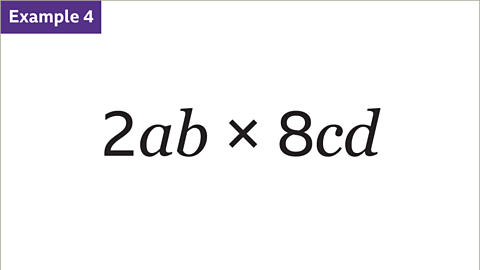
Image caption, The terms 2𝒂𝒃 and 8𝒄𝒅 are multiplied. Simplify 2𝒂𝒃 × 8𝒄𝒅
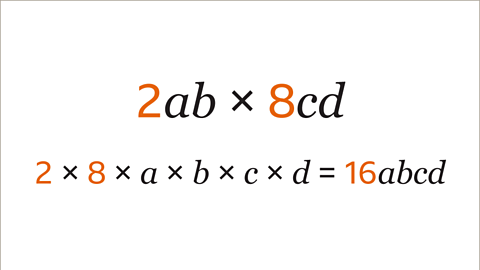
Image caption, Multiply the constants (2 and 8) to find the coefficient of the simplified term (16). 2 x 8 = 16. Different variables (𝒂, 𝒃, 𝒄 and 𝒅) are written next to each other in alphabetical order (𝒂𝒃𝒄𝒅). 2𝒂𝒃 × 8𝒄𝒅 simplifies to the term 16𝒂𝒃𝒄𝒅
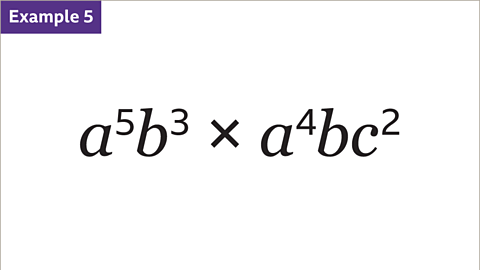
Image caption, The terms 𝒂⁵𝒃³ and 𝒂⁴𝒃𝒄² are multiplied. Simplify 𝒂⁵𝒃³ × 𝒂⁴𝒃𝒄²
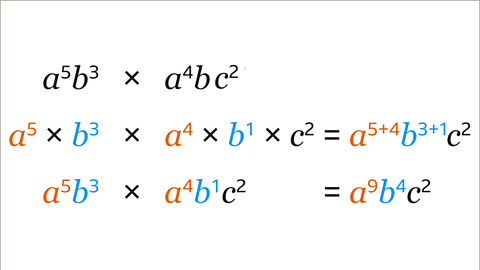
Image caption, Multiply matching variables using the laws of indices. In multiplication, the indices are added. 𝒂⁵ × 𝒂⁴ ⁼ 𝒂⁹ , 𝒃³ × 𝒃 ⁼ 𝒃⁴. Different variables (𝒂⁹, 𝒃⁴ and 𝒄²) are written next to each other in alphabetical order. The simplified term is 𝒂⁹𝒃⁴𝒄²
1 of 10
Questions
Question 1: Simplify the terms using multiplication.
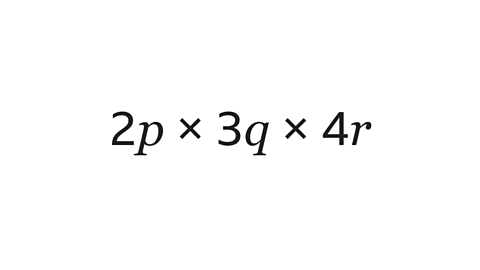
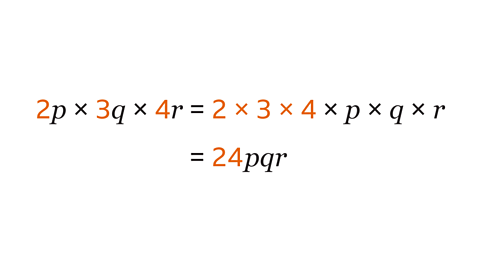
Multiply the constants to find the coefficient of the simplified term:
2 × 3 × 4 = 24Write the different variables (\(p\), \(q\) and \(r\)) next to each other in alphabetical order: \(pqr\)
The simplified term is 24 \(pqr\)
Question 2: Simplify the terms using multiplication.
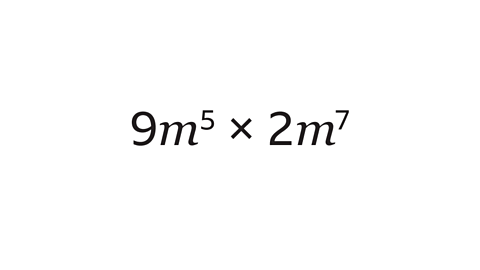
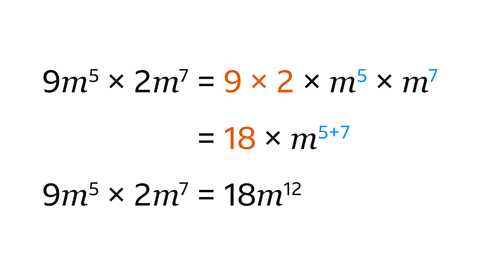
Multiply the constants to find the coefficient of the simplified term:
9 × 2 = 18Multiply the matching variables using the laws of indices.
Add the indices: \(m\)⁵ × \(m\)⁷ ⁼ \(m\)¹²
The simplified term is 18\(m\)¹²
Simplifying terms by dividing
To simplify terms using division:
Write the division as a fraction. The dividendIn division, the number that is divided. Eg, in the calculation 30 ÷ 6, 30 is the dividend. is the numeratorNumber written at the top of a fraction. The numerator is the number of parts used. Eg, for 1⁄3, the numerator is 1 and the divisorThe number by which another is divided. Eg, in the calculation 30 ÷ 6 , the divisor is 6 is the denominatorNumber written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1⁄3, the denominator is 3.
Divide the constants to find the coefficient of the term. This will give an integerIntegers are numbers with no fraction or decimal part. They can be positive, negative or zero. 42, 8, and 10000 are examples of integers. coefficient or a fraction which is simplified by dividing the numerator and the denominator by their highest common factor (HCF) The largest factor that will divide into the selected numbers. Eg, 10 is the highest common factor of 30 and 20. Highest common factor is written as HCF. .
Divide the matching variables using the laws of indices. The index of the divisor is subtracted from the index of the dividend.
When simplifying terms, it's helpful to remember that:
when there is no written index, the index is always 1
any number or expression raised to the power of zero is always equal to 1
Examples
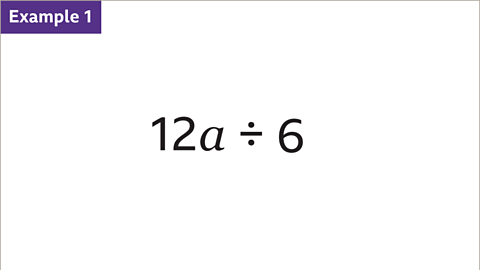
Image caption, The term 12𝒂 is divided by the term 6. Simplify 12𝒂 ÷ 6

Image caption, Write the division as a fraction. The dividend (12𝒂) is the numerator and the divisor (6) is the denominator. Divide the constants to find the coefficient of the term (12 ÷ 6 = 2). Write the coefficient in front of the variable (𝒂). The simplified term is 2𝒂
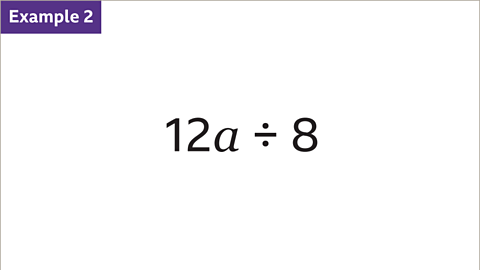
Image caption, The term 12𝒂 is divided by the term 8. Simplify 12𝒂 ÷ 8
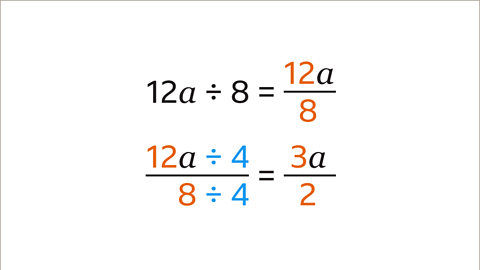
Image caption, Write the division as a fraction. Simplify the fraction 12⁄8. The HCF of 12 and 8 is 4. Divide 12 and 8 by 4. The fraction simplifies to 3⁄2. Write the coefficient in front of the variable, 𝒂. The simplified term is 3𝒂/2

Image caption, The term 𝒂¹¹ is divided by the term 𝒂³. Simplify 𝒂¹¹ ÷ 𝒂³
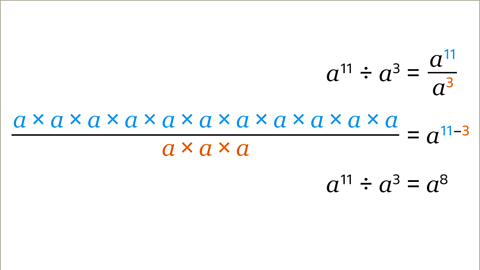
Image caption, Write the division as a fraction. The dividend (𝒂¹¹) is the numerator and the divisor (𝒂³) is the denominator. Divide the matching variables using the laws of indices. The index of the divisor is subtracted from the index of the dividend to give the index of the simplified term (11 – 3 = 8). The simplified term is 𝒂⁸

Image caption, The term 15𝒂⁶ is divided by the term 3𝒂². Simplify 15𝒂⁶ ÷ 3𝒂²
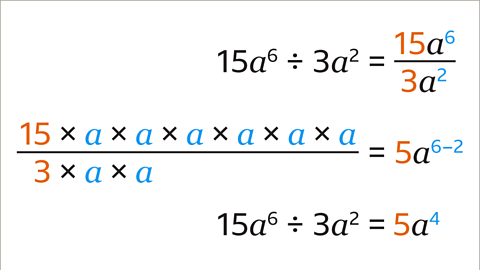
Image caption, Write the division as a fraction. The dividend (15𝒂⁶) is the numerator and the divisor (3𝒂²) is the denominator. Divide the constants to find the coefficient of the term (15 ÷ 3 = 5). Divide the matching variables using the laws of indices. The index of the divisor is subtracted from the index of the dividend to give the index of the simplified term (6 – 2 = 4). The simplified term is 5𝒂⁴
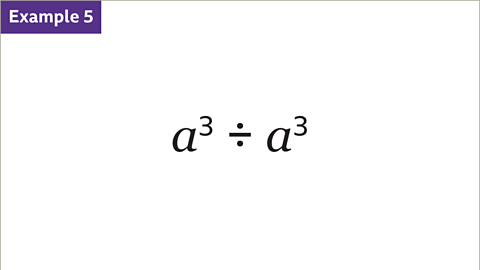
Image caption, The term 𝒂³ is divided by the term 𝒂³. Simplify 𝒂³ ÷ 𝒂³
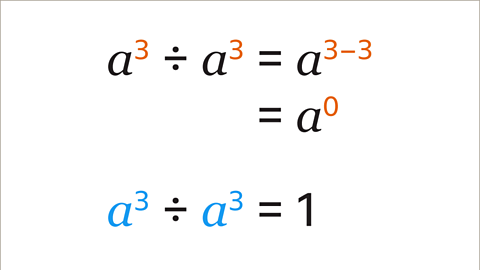
Image caption, Divide the matching variables using the laws of indices. The index of the divisor is subtracted from the index of the dividend to give the index of the simplified term (3 – 3 = 0). This gives 𝒂⁰. Remember that any number or expression raised to the power of zero is always equal to 1. 𝒂³ is being divided by itself. 𝒂³ ÷ 𝒂³ = 1
1 of 10
Question
Simplify the expression.
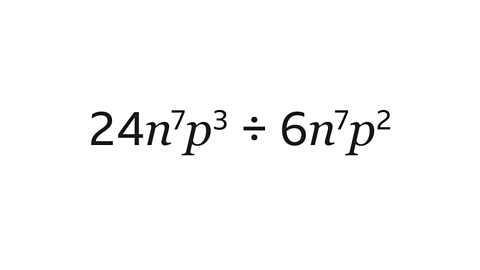
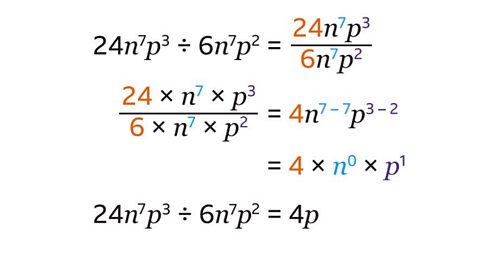
Write the division as a fraction.
- The dividend (24\(n\)⁷\(p\)³) is the numerator and the divisor (6\(n\)⁷\(p\)²) is the denominator.
Divide the constants to find the coefficient of the term (24 ÷ 6 = 4).
Divide the matching variables using the laws of indices.
Subtract the index of the divisor from the index of the dividend to give the index of the simplified term:
\(n\)⁷ ÷ \(n\)⁷ = \(n\)⁷⁻⁷ = \(n\)⁰ = 1
\(p\)³ ÷ \(p\)² = \(p\)³⁻² = \(p\)¹ = \(p\)
The simplified term is 4\(p\)
Practise simplifying terms by multiplying and dividing
Quiz
Practise simplifying terms using multiplication and division with this quiz. You may need a pen and paper to help you work out your answers.
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Expressions and formulae
Find out more by working through a topic
- count5 of 8
- count7 of 8
- count8 of 8