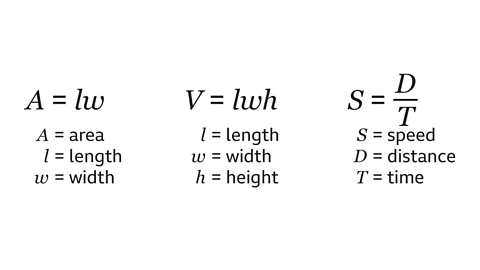Key points
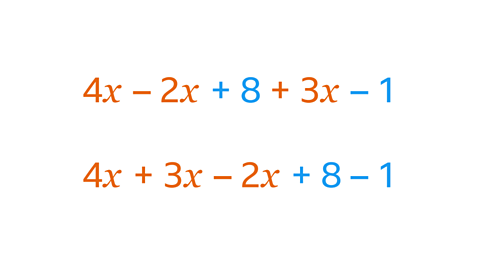
In algebraic expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms., letters represent unknown numbers (variableAn unknown value, usually represented by a letter like 𝒙 or 𝒚). A variable can have many values or sometimes just one.
An algebraic expression may be simplifyRewrite an expression so that it has fewer terms. An expression may be simplified using addition, subtraction, multiplication or division. by collecting like termsTerms whose variables (such as 𝒙 or 𝒚) with any exponents (a symbol written above and to the right of a mathematical expression) are the same. For example, 7𝒙 and 2𝒙 are like terms because they are both amounts of ‘𝒙’.. To reduce the number of termAn element within an algebraic sentence. Elements (terms) are separated by + or - signs. in the expression, like terms are added or subtracted.
Like terms may be constantA number or quantity that does not vary. A constant speed is a steady speed. Eg, the speed of light is constant. The speed of a car is not constant, it varies. (number values), a quantity of the same variable or the same combination of variables.
When grouping the like terms together, the order does not matter. However, the positive like terms are often written before the negative like terms.
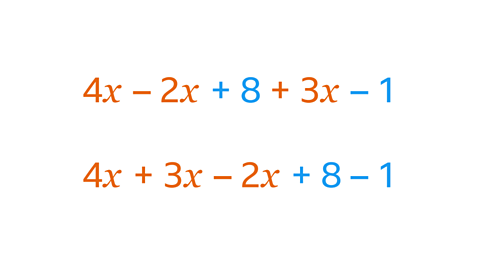
Video
Watch the video to learn about collecting like terms to simplify expressions.
An expression is the sum of one or more terms.
4𝑎 plus 2𝑏 plus 2𝑎 minus 𝑏 plus 3 is an expression using five terms. 4𝑎, 2𝑏, 2𝑎, 𝑏 and 3.
The number 3 is called a constant and the letters are called variables. 4𝑎 and 2𝑎 are like terms. So are 2𝑏 and 𝑏. 4𝑎 and 2𝑏 are unlike terms because they have different variables.
The number in front of the letter is called the coefficient. 4𝑎 means four lots of 𝑎. So, our original expression could be expressed like this, but grouping like terms together makes it easier to understand.
This is called collecting like terms. Collecting like terms helps simplify the expression without changing its value, making it easier to work with.
Look at the original expression, it can be simplified further by collecting our like terms. The first step is to group like terms together, taking care to keep the sign before each variable.
4𝑎 plus 2𝑎 is 6𝑎. 2𝑏 minus 𝑏 is 𝑏 and 3 stays 3. Now the expression is three terms instead of five, which simplifies it.
When you're adding and subtracting always keep the plus or minus sign before the term. So 2𝑏 minus 2𝑐 minus 𝑏 would be 𝑏 minus 2𝑐.
Here's one more example to simplify. It's always important to keep the sign in front of the variable when collecting like terms. It's worth reviewing how to add negative numbers if you're not sure.
So that's 4𝑐 minus 3𝑑 plus 2𝑒.
Recognising and collecting like terms
To recognise like termsTerms whose variables (such as 𝒙 or 𝒚) with any exponents (a symbol written above and to the right of a mathematical expression) are the same. For example, 7𝒙 and 2𝒙 are like terms because they are both amounts of ‘𝒙’., look carefully at each term. Like terms may be:
- constantA number or quantity that does not vary. A constant speed is a steady speed. Eg, the speed of light is constant. The speed of a car is not constant, it varies. (number values)
- terms that use matching variableAn unknown value, usually represented by a letter like 𝒙 or 𝒚
- terms that use matching combinations of variables
Once like terms are identified, they can be collected and grouped together. The expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms. is then ready to be simplified.
Examples
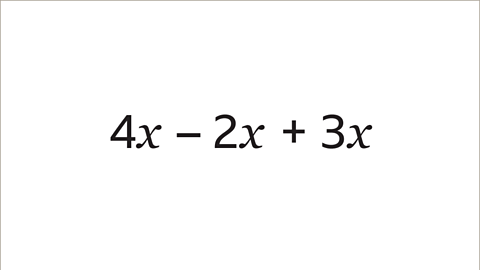
Image caption, 4𝒙, – 2𝒙 and 3𝒙 are like terms. They are all amounts of 𝒙
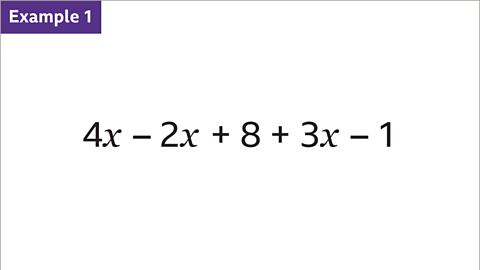
Image caption, Identify the like terms in this expression.
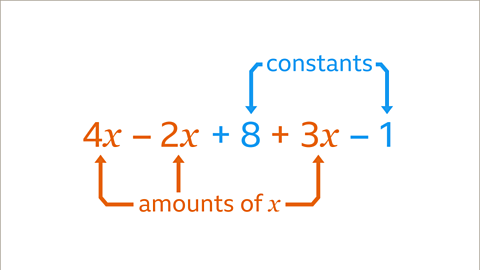
Image caption, There are two groups of like terms in the expression. 4𝒙, 3𝒙 and – 2𝒙 are like terms as they are all amounts of the same variable, 𝒙. 8 and – 1 are like terms as they are both constants.
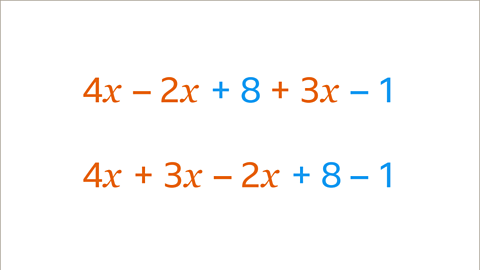
Image caption, The like terms are collected. The sign in front of each term stays with that term. The – 2𝒙 stays as – 2𝒙. The 3𝒙 stays as 3𝒙. The + 8 stays as + 8. The – 1 stays as – 1. It is helpful to write the positive like terms before the negative like terms. This expression with the collected like terms is 4𝒙 + 3𝒙 – 2𝒙 + 8 – 1
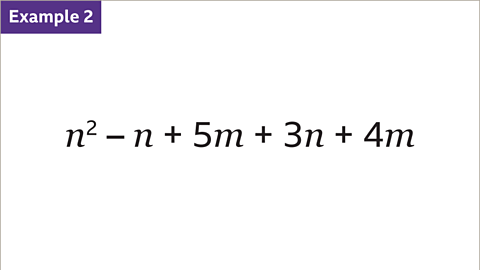
Image caption, Identify the like terms in this expression.
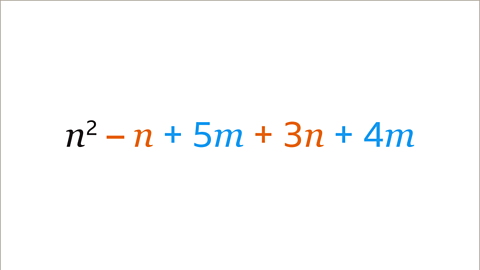
Image caption, There are two groups of like terms in the expression. – 𝒏 and 3𝒏 are like terms. They are both amounts of the same variable, 𝒏. 5𝒎 and 4𝒎 are like terms. They are both amounts of the variable, 𝒎. 𝒏² is not the same as any other term in the expression. The like terms can be collected.
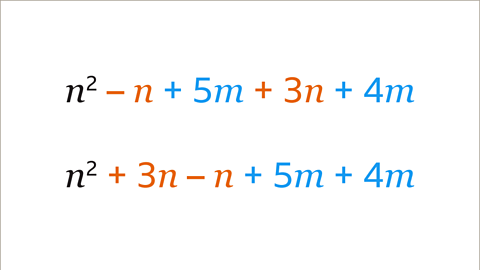
Image caption, The like terms are collected. The sign in front of each term stays with that term. The + 3𝒏 stays as + 3𝒏. The – 𝒏 stays as – 𝒏. The + 5𝒎 stays as + 5𝒎. The + 4𝒎 stays as + 4𝒎. It is helpful to write the positive like terms before the negative like terms. This expression written with collected like terms is 𝒏² + 3𝒏 – 𝒏 + 5𝒎 + 4𝒎
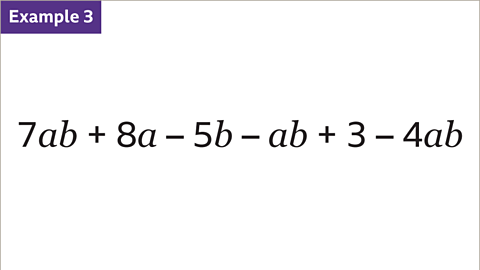
Image caption, Identify the like terms in this expression.
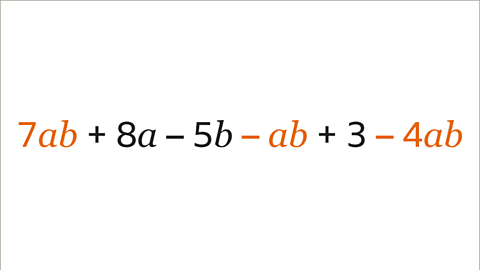
Image caption, There is one group of like terms in the expression. 7𝒂𝒃, – 𝒂𝒃 and – 4𝒂𝒃 are like terms as they are all amounts of the same combination of variables, 𝒂𝒃. The remaining terms are not the same as any other term in the expression (8𝒂, – 5𝒃 and 3). The like terms can be collected.
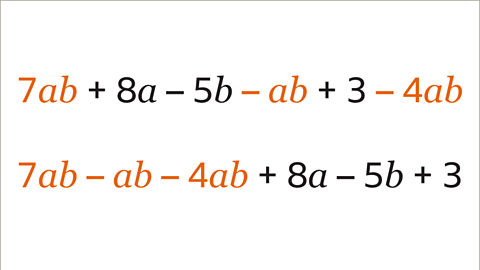
Image caption, The like terms are collected. The sign in front of each term stays with that term. The 7𝒂𝒃 stays as 7𝒂𝒃. The – 𝒂𝒃 stays as – 𝒂𝒃. The – 4𝒂𝒃 stays as – 4𝒂𝒃. This expression written with collected like terms is 7𝒂𝒃 – 𝒂𝒃 – 4𝒂𝒃 + 8𝒂 – 5𝒃 + 3
1 of 10
Question
Identify the like terms in the expression 3𝒙 – 1 + 𝒙 + 10
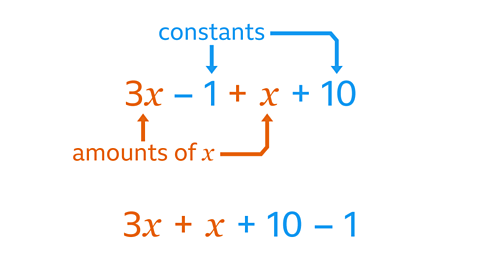
There are two groups of like terms:
- -1 and 10 are like terms because they are both constants.
- 3𝒙 and 𝒙 are like terms because they are both a quantity of the variable 𝒙
The like terms can be collected.
The positive like terms are written before the negative like terms, giving
3𝒙 + 𝒙 + 10 – 1
Simplifying expressions by collecting like terms
- To simplify expressions by collecting like terms:
Identify and collect the like terms.
Combine the like terms.
Add or subtract the like terms according to the symbols in the expression.
- The simplified expression is equivalent to the original expression. They are identity ≡An equation that is true no matter what values are chosen. The identity symbol ≡ links expressions that are identities..
Examples
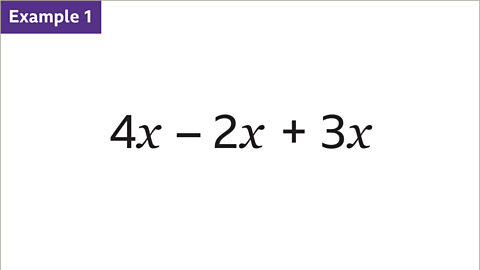
Image caption, Simplify the expression.
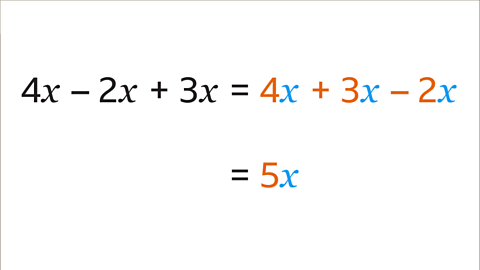
Image caption, 4𝒙, – 2𝒙 and 3𝒙 are like terms, they are all amounts of 𝒙. They can be collected, writing the positive terms first (4𝒙 and 3𝒙) followed by the negative term (– 2𝒙). The expression can be simplified: 4𝒙 + 3𝒙 – 2𝒙 = 5𝒙
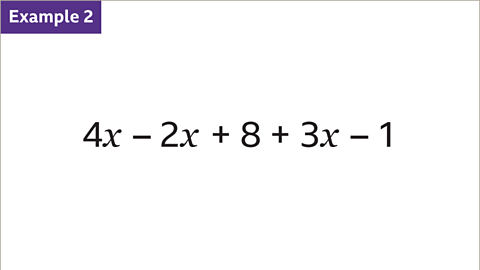
Image caption, Simplify the expression.
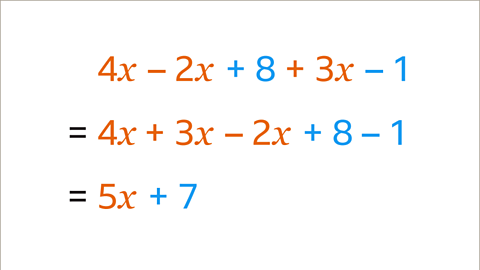
Image caption, There are two groups of like terms in the expression. 4𝒙, 3𝒙 and – 2𝒙 are like terms and 8 and – 1 are like terms. The like terms are collected and the symbol before each term is moved with each term. The positive like terms are written before the negative like terms. The expression can be simplified by adding the like terms. 4𝒙 + 3𝒙 – 2𝒙 = 5𝒙 and 8 – 1 = 7. The simplified expression is 5𝒙 + 7
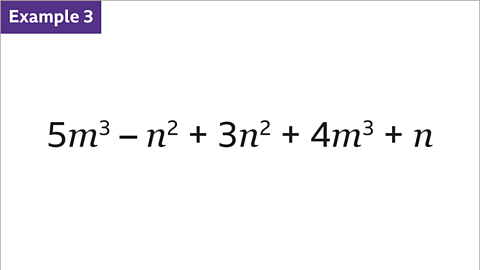
Image caption, Simplify the expression.
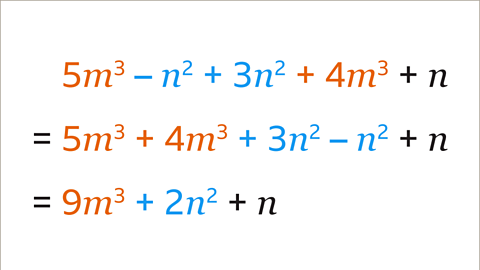
Image caption, There are two groups of like terms in the expression, amounts of 𝒎³ and amounts of 𝒏². 𝒏 is not the same as any other term in the expression. The like terms are collected and the symbol before each term is moved with each term. The expression 5𝒎³ + 4𝒎³ + 3𝒏² – 𝒏² + 𝒏 simplifies to 9𝒎³ + 2𝒏² + 𝒏
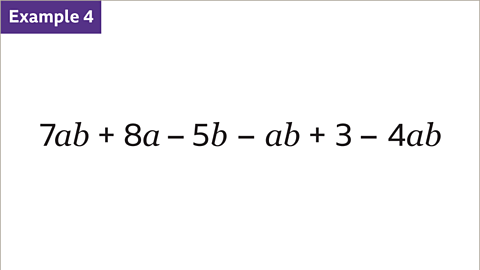
Image caption, Simplify the expression.
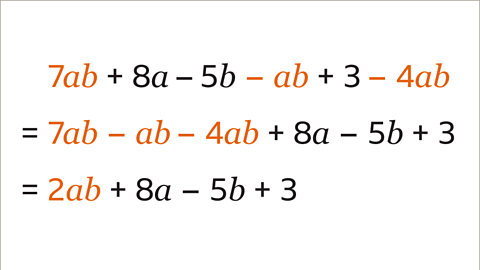
Image caption, There is one group of like terms in the expression, amounts of 𝒂𝒃. The remaining terms are not the same as any other term. The like terms are collected and the symbol before each term is moved with each term. The positive like terms are written before the negative like terms. The expression 7𝒂𝒃 – 𝒂𝒃 – 4𝒂𝒃 + 8𝒂 – 5𝒃 + 3 simplifies to 2𝒂𝒃 + 8𝒂 – 5𝒃 + 3
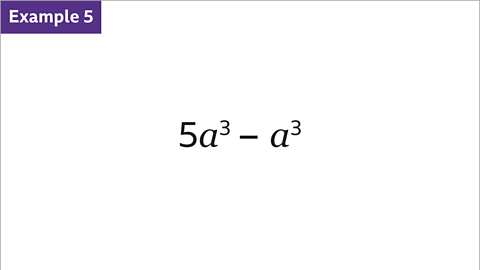
Image caption, Simplify the expression.
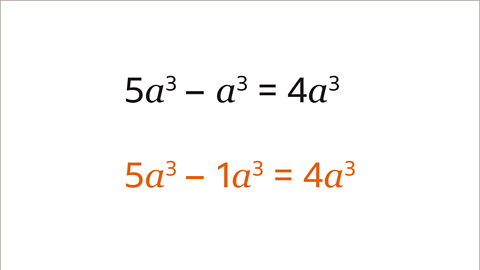
Image caption, The two terms are like terms as they are both amounts of the same variable (𝒂³). Variables with no number have a coefficient (a number or symbol multiplied with a variable or an unknown quantity in an algebraic term) of 1, so the term 𝒂³ is one 𝒂³. 5𝒂³ – 1𝒂³ = 4𝒂³
1 of 10
Question
Simplify the expression by collecting the like terms.
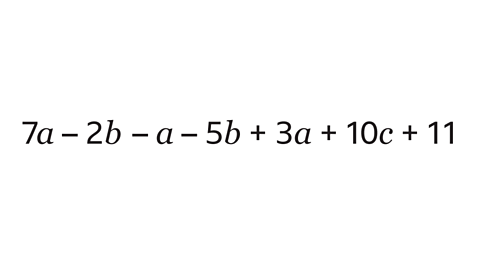
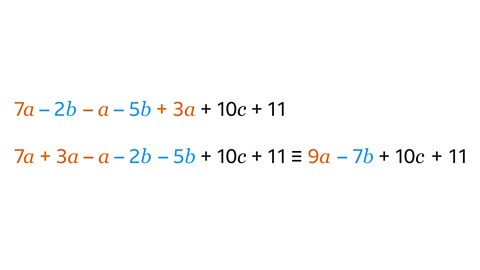
Identify the like terms:
- 7𝒂, – 𝒂 and 3𝒂 are like terms.
- – 2b and – 5b are like terms.
Collect the like terms, making sure the symbol in front of each term moves with it.
Write the positive like terms before the negative like terms.
- The expression becomes 7𝒂 + 3𝒂 – 𝒂 – 2𝒃 – 5𝒃 + 10𝒄 + 11
Simplify (add or subtract) according to the symbols in the expression:
- 7𝒂 + 3𝒂 – 𝒂 = 9𝒂
- 2𝒃 – 5𝒃 = – 7𝒃
The simplified expression is equivalent to the original expression. They are identities.
7𝒂 + 3𝒂 – 𝒂 - 2𝒃 – 5𝒃 + 10𝒄 + 11 ≡ 9𝒂 – 7𝒃 + 10𝒄 + 11
Practise collecting like terms
Practise collecting like terms with this quiz. You may need a pen and paper to help you.
Quiz
Real-life maths

Collecting like terms is about totalling the amounts of the same item.
A buyer (a person who chooses what type of goods will be sold by a company) working for a group of clothes shops will add up the sales of different sizes of the same item of clothing, eg a jumper. This is not only to find out total sales but also to help them work out buying needs in the future.
This is necessary because if the buyer just adds up sales based on something simply being 'a jumper’, and not considering its different sizes, this would be unhelpful as not everyone wears the same size. Different sizes are not counted together as they are not 'like sizes'. Businesses need to be able to stock items according to what different customers require.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Expressions and formulae
Find out more by working through a topic
- count5 of 8
- count7 of 8