4 anciens problèmes mathématiques qui ont montré que l'impossible est possible

Crédit photo, Getty Images
- Author, Dalia Ventura
- Role, BBC News World
Il s'agit des problèmes classiques des mathématiques anciennes, qui ont le charme de paraître simples. En réalité, leur résolution n'est pas difficile, mais impossible.
Il a fallu des millénaires pour le prouver, des siècles au cours desquels des sommités telles qu'Euclide, Archimède, René Descartes, Isaac Newton et Carl Friedrich Gauss, ainsi que des artistes et des intellectuels, ont tenté de trouver un moyen de les résoudre.
Ses explorations, cependant, n'étaient pas vaines, mais inspirantes et ont favorisé le développement des mathématiques.
On ne sait pas avec certitude comment elles sont nées, mais la plus célèbre d'entre elles, la recherche de la quadrature du cercle, par exemple, apparaît déjà dans le papyrus Rhind, un document datant d'environ 4 000 ans et provenant de l'Égypte ancienne.
Ce que l'on sait, c'est que ce sont les Grecs de l'Antiquité qui les ont posées avec précision en termes mathématiques.
Des informations vérifiées à portée de main
Cliquez ici et abonnez-vous !
Fin de Promotion WhatsApp
En bref, les défis à relever étaient les suivants :
quadrature du cercle
la trisection d'un angle
Le doublement du cube
L'inscription de tous les polygones réguliers dans un cercle
Exprimés ainsi, ils sont peut-être déroutants, mais ce qu'ils nous demandent en réalité, c'est...
Tracer un carré dont l'aire est la même que celle d'un cercle donné
Diviser un angle en trois angles égaux
Dessiner un cube deux fois plus grand qu'un autre
Diviser un cercle en parties égales
Mieux vaut ne pas le faire ?
Mais comme l'a dit l'écrivain Donald Westlake, "chaque fois que quelque chose semble facile, il s'avère qu'il y a une partie que vous n'avez pas entendue"... ou, dans le cas présent, que nous n'avons pas dite.
Pour relever ces défis, vous ne pouvez le faire qu'à la manière de la Grèce antique, c'est-à-dire qu'en plus d'un objet à dessiner, d'un objet sur lequel dessiner et de votre esprit, vous ne pouvez utiliser qu'un compas et une règle sans marques.

Pourquoi ?
"C'est une bonne question. Et il y a plusieurs réponses", a déclaré à BBC Mundo le mathématicien David Richeson, auteur de "Tales of Impossibility". "(en français : Récits de l'impossibilité).
"L'une d'entre elles est que le compas et la règle sont clairement inscrits dans les postulats du livre fondamental des mathématiques d'Euclide, les Éléments (~300e siècle av. J.-C.).
"Une autre réponse est qu'ils représentent les outils les plus élémentaires qui ont toujours été utilisés. Avec une corde, on peut obtenir une ligne droite, et si l'on fixe une extrémité au sol, on peut tracer un cercle avec l'autre.
"Mais aussi pour sa simplicité et son élégance. Pour moi, ce qui est surprenant, ce n'est pas tant ce que l'on ne peut pas faire que tout ce que l'on peut faire avec ces outils".
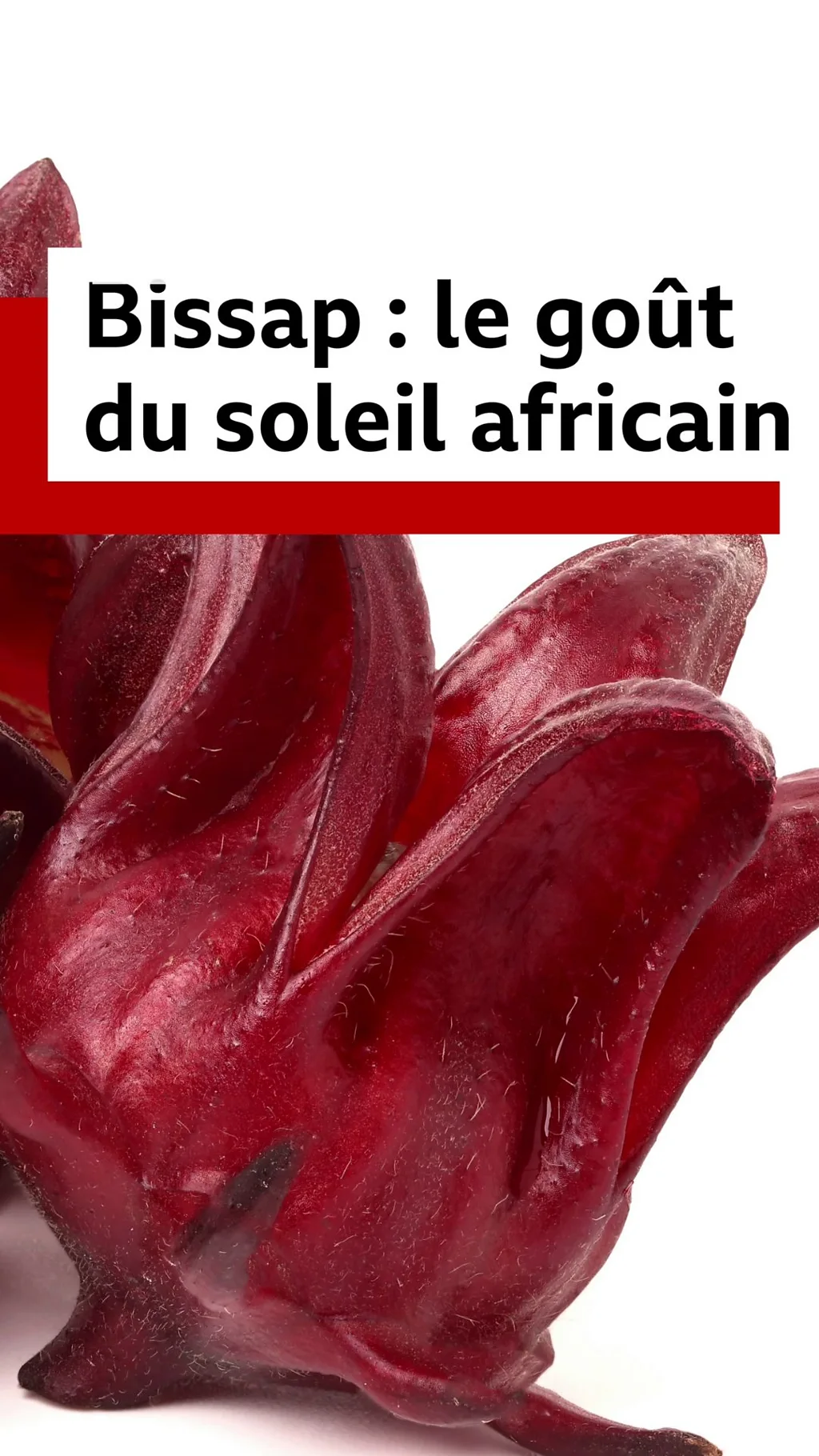
Vous pouvez, par exemple, couper un angle (le diviser en deux angles égaux) facilement.
"La bissection d'un angle est quelque chose que nous apprenons à l'école en cours de géométrie. "C'est très simple", explique M. Richeson.
"Mais la question qui intéressait les Grecs était la suivante : si vous avez un angle, pouvez-vous le diviser en trois parties égales ?
"La réponse était : parfois oui, mais il n'y a pas de règle générale sur la façon de le faire".
Et il précise : "Cela ne signifie pas que ces problèmes sont impossibles, quels que soient les outils utilisés. Mais avec ces outils euclidiens classiques, ils sont impossibles à résoudre".
Archimède, l'un des plus grands mathématiciens de l'histoire, a montré que si la règle n'avait que deux marques, une distance pouvait être mesurée exactement, et cela suffisait pour pouvoir tricoter n'importe quel angle, explique M. Richeson.
" Donc si vos outils étaient un peu plus sophistiqués, vous pourriez résoudre ces problèmes ".
Mais le jeu n'en vaut pas la chandelle : le défi est de le faire en respectant les règles du jeu, un jeu irrésistible pour les esprits brillants...< /span>.
Tentatives multiples
La première tentative connue de résoudre la quadrature du cercle est celle d'Anaxagore, mathématicien grec célèbre pour avoir été le premier à introduire la philosophie à Athènes, au Ve siècle avant J.-C. Il a été emprisonné pour avoir affirmé que le Soleil n'était pas un dieu mais un rocher brûlant et que la Lune reflétait sa lumière.
Selon l'historien Plutarque, il était en prison pour avoir affirmé que le Soleil n'était pas un dieu mais un rocher brûlant au rouge et que la Lune reflétait sa lumière.
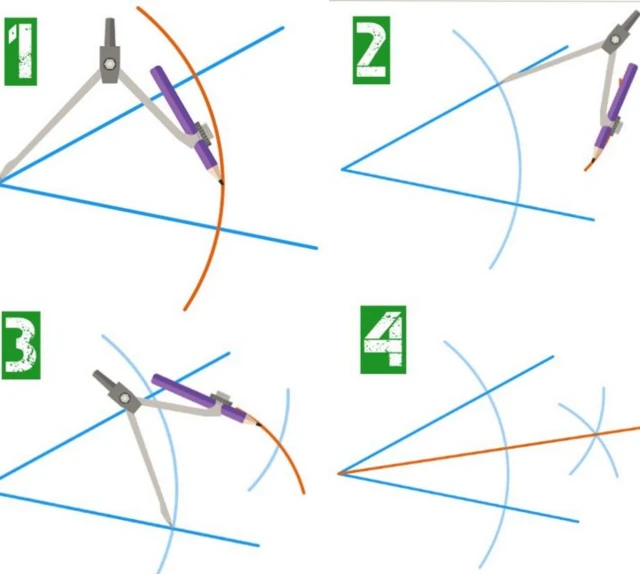
Il passait ces journées à essayer en vain de construire, avec seulement un compas et une règle, un carré ayant la même surface qu'un cercle.
Son contemporain, Hippocrate de Chios, l'un des mathématiciens dont les travaux ont été synthétisés dans la géométrie euclidienne, parvient à une solution partielle encourageante : la lune (ou lunule) d'Hippocrate, premier carré d'une figure curviligne de l'histoire.
Il faudra attendre 23 siècles pour que le grand mathématicien et physicien suisse Leonhard Euler trouve, en 1771, deux nouveaux types de lunes quadruples qui, toutefois, ne contribueront pas à la quadrature du cercle, comme on le pensait autrefois.
Ce n'est que le début de la longue liste de mathématiciens et d'amateurs qui ont relevé le défi armés de ces deux seuls outils.
"Léonard de Vinci a traversé une période où il était vraiment fasciné par les mathématiques et la géométrie, et il a essayé de résoudre ces problèmes, mais il a aussi intégré son talent artistique pour créer des dessins avec ces outils", explique M. Richeson.
Crédit photo, Getty Images
Et il n'est pas le seul homme de la Renaissance à s'y être essayé.
L'artiste le plus célèbre de la Renaissance allemande, Albrecht Dürer, était également l'un des plus importants mathématiciens de l'époque.
Dans le deuxième livre de son ouvrage "Les quatre livres de mesure", il donne des méthodes approximatives pour résoudre la quadrature du cercle à l'aide de constructions à la règle et au compas.
Il a également fourni une méthode permettant d'obtenir une bonne approximation du trisecteur d'un angle à l'aide d'outils euclidiens.
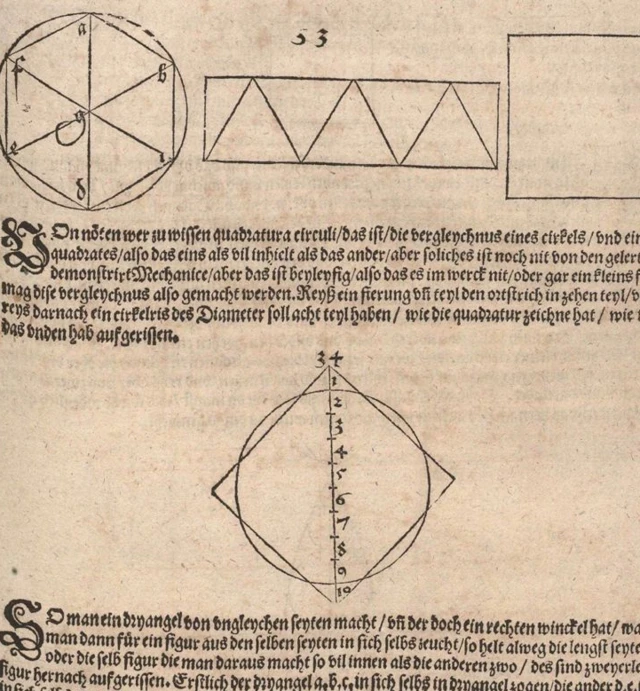
Pour Richeson, l'une des histoires les plus fascinantes est celle de la construction de polygones réguliers ou, ce qui revient au même, de la division du cercle en parties égales.
"Ce problème a toujours été notoirement compliqué : nous savions en construire plusieurs, mais pas tous.
"Certains, comme les polygones à 7, 9 et 17 côtés, étaient inconnus et pendant de nombreuses années, les gens se sont demandé s'ils étaient impossibles", a-t-il déclaré à BBC Mundo.
De l'époque de la Grèce classique jusqu'à la fin du XVIIIe siècle, il n'y a pas eu de progrès significatifs, en utilisant uniquement les outils euclidiens.
Jusqu'à l'arrivée du prodige des mathématiques Carl Gauss.
"En 1796, Gauss, qui n'était alors qu'un adolescent mais qui est devenu l'un des mathématiciens les plus célèbres de l'histoire, a démontré qu'il était possible de construire un polygone régulier de 17 côtés.
"C'était l'une de ses premières découvertes, et c'était quelque chose qui avait été impossible pour des générations de mathématiciens".
En outre, il faut tenir compte du fait que, ces problèmes n'étant pas pratiques mais théoriques, la preuve de leur résolution est plus importante que la résolution elle-même.
Et l'analyse approfondie que Gauss a effectuée pour prouver sa découverte a ouvert la voie aux idées ultérieures de la théorie de Galois.
Ainsi, si vous vous demandiez quel était l'intérêt de voir tant de brillants esprits s'efforcer de réaliser ce qui, dans plusieurs cas, était possible avec d'autres outils, voici un exemple du processus de retour d'information qui a permis de produire de plus en plus de connaissances.
"Essayer de résoudre ces problèmes a vraiment fait avancer les mathématiques, mais aussi, au fur et à mesure que de nouvelles mathématiques étaient développées, les gens revenaient à ces anciens problèmes pour voir si ce qui avait été découvert permettait de les résoudre.
"C'était une sorte de va-et-vient au fil des siècles", explique l'expert.
Tout n'est pas possible

Crédit photo, Getty Images
Si tenter de résoudre ces problèmes a contribué au progrès des mathématiques, prouver qu'il était possible de le faire dépendait de ce progrès.
"Il a fallu attendre l'invention de la géométrie analytique, de l'algèbre, du calcul, des nombres complexes, d'une compréhension approfondie de π et même de la théorie des nombres, ce qui explique en partie pourquoi cela a pris autant de temps.
Dans le cas de la quadrature du cercle, par exemple, "le coup de grâce a été donné lorsqu'on a découvert que π était un nombre transcendant".
Après des siècles d'une obsession à laquelle les Grecs de l'Antiquité avaient déjà donné un nom -tetragonidzein ou quadrature du cercle-, tout s'est arrêté.
Il ne s'agissait pas seulement d'une ambition de sommités plus ou moins célèbres, qui ont fait profiter la connaissance de leurs efforts.
Des milliers de personnes ont souffert au fil des ans de ce que le mathématicien Augustus De Morgan a appelé au XIXe siècle le morbus cyclometricus ou la maladie de la quadrature du cercle qui, selon lui, touchait les enthousiastes mal informés.
Parmi eux, un comptable et mathématicien argentin amateur du nom d'Elías O'Donnell.
En 1870, il a publié un livre avec "la conscience la plus intime que, dans ce traité, la résolution exacte souhaitée de la quadrature du cercle est démontrée de la manière la plus convaincante et la plus rigoureuse", comme il l'a déclaré sur la première page.
"Et quelle que soit la gravité de cette phrase, elle sera la vérité pour tous les siècles de la postérité", ajoutait-il. a>

Cependant, depuis 1801, on savait, grâce à Gauss, que si π (l'aire d'un cercle de rayon 1) était transcendant, la quadrature du cercle serait impossible.
Et en 1882, l'Allemand Carl Louis Ferdinand von Lindemann a démontré que <a i=4>, en effet, π était un nombre transcendant.
45 ans plus tôt, le mathématicien français Pierre Wantzel (1814-1848) avait déjà prouvé dans une seule des 7 pages d'un article que les trois autres problèmes étaient impossibles à résoudre.
Tout cela est étonnant, car prouver que quelque chose est impossible est extrêmement difficile... et important.
"Généralement, lorsque nous pensons à quelque chose d'impossible, nous pensons que c'est très difficile, ou que cela peut prendre beaucoup de temps, ou quelque chose de ce genre.
"Mais lorsqu'un mathématicien prouve qu'une chose est impossible, cela signifie que, d'un point de vue logique, elle ne peut pas se produire : il n'y a pas moyen de faire la trisectrice d'un angle général. Il n'y a pas moyen de faire la trisection d'un angle général. Il n'y a pas moyen de faire la quadrature du cercle.
Il ne s'agit pas seulement de dire "nous ne sommes pas assez intelligents", "nous n'avons pas fait assez d'efforts" ou "nous avons besoin de plus de temps". Il s'agit de : Il s'agit de savoir jusqu'où nous sommes allés : c'est impossible", souligne M. Richeson.
"Il y a beaucoup de théorèmes d'impossibilité célèbres en mathématiques, et ils sont tous très vénérés, parce qu'on a prouvé une chose négative : que quelque chose qui n'est pas cela peut se produire. Il s'agit là d'une réussite incroyable.

Crédit photo, Getty Images
Cela ne veut pas dire que les gens abandonnent
En 1897, par exemple, le Sénat de l'Indiana a examiné un projet de loi visant à légaliser une méthode de quadrature du cercle découverte par le médecin et mathématicien amateur Edwin L. Goodwin.
La loi qui visait à "introduire une nouvelle vérité mathématique" fut d'abord acceptée par une commission mais finalement rejetée.
Et l'on dit qu'il n'y a pas de mathématicien disposant d'un courriel qui n'ait reçu des solutions de quadratures de cercle, de duplicateurs de cubes ou de trisecteurs d'angles convaincus d'avoir trouvé la solution.
"Ils insistent sur cette incompréhension de ce que signifie l'impossible", dit Richeson.
C'est aussi parce qu'"ils sont faciles à décrire et à manipuler", qu'ils essaient, qu'ils croient les avoir résolus "et qu'ils envoient les solutions aux mathématiciens des universités".
"Il est garanti qu'il y aura une erreur quelque part, qu'il s'agisse des mathématiques ou des règles. Ils ont donc peut-être trouvé un moyen de résoudre l'un de ces problèmes, mais pas en utilisant les règles classiques".
Euclide a construit tout un palais de sagesse et fécondé d'autres idées, car ses contemporains et les générations suivantes ont continué à essayer de promouvoir la connaissance en n'utilisant, comme lui, qu'un compas et une règle.
Dans le cas de ces quatre problèmes, il est possible que, depuis la Grèce classique, on ait soupçonné qu'ils n'étaient pas viables, mais il était très enrichissant d'essayer.