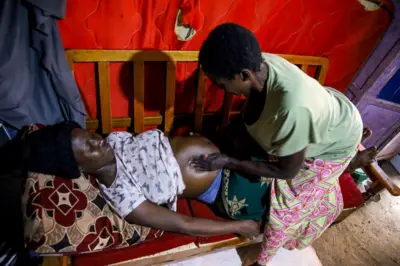
Le problème des "écolières de Kirkman" qui fascine les mathématiciens depuis 172 ans

Crédit photo, Getty Images
- Author, Margarita Rodríguez
- Role, BBC News Mundo
Imaginez que votre augmentation de salaire tant attendue dépend de votre capacité à ne faire qu’une seule chose.
Votre chef organise un congrès et a confirmé la présence de sept grands experts qui débattront entre eux lors de tables rondes.
Et elle vous demande que chaque table n’ait que trois débatteurs.
Jusqu’ici, tout va bien, non? Vous consultez déjà votre compte bancaire ?
Mais au cours de la conversation avec les débatteurs, vous découvrez un détail : ils sont les meilleurs dans leur domaine, mais ils ne s’entendent pas les uns avec les autres – et chacun, à sa manière, impose une condition :
« Je peux assister au congrès si le besoin est exprimé, mais je veux être présent à côté des six autres invités une seule fois, ni plus, ni moins. »
Cela semble difficile, mais ne désespérez pas.
Ce que votre patron demande est très similaire à la question posée par le mathématicien britannique Thomas Kirkman en 1850. L’équation est connue sous le nom de problème collégial.
Avec l’aide du professeur de mathématiques Raúl Ibáñez, de l’Université du Pays Basque en Espagne, nous vous dirons de quoi il s’agit.
« Le problème des écolières fascine les gens depuis longtemps. Cela ressemble à un puzzle, une énigme, mais il a des aspects très profonds », explique Ibáñez, qui est un diffuseur scientifique et auteur de plusieurs livres et articles sur les mathématiques. Un de ses livres consacre un chapitre à ce problème.
« Cela semble facile, mais c’est intrinsèquement très compliqué, et sa résolution n’est pas toujours simple », dit-il.
Théorie des groupes
Kirkman est né à Manchester, en Angleterre, en 1806.
Un enseignant a révélé qu’ à l’école, il avait le potentiel d’être accepté à l’Université de Cambridge, mais son père avait d’autres projets pour lui.

Crédit photo, Getty Images
Des informations vérifiées à portée de main
Cliquez ici et abonnez-vous !
Fin de Promotion WhatsApp
« Thomas a été forcé d’abandonner l’école à l’âge de 14 ans et d’aller travailler dans le bureau de son père », selon les professeurs John Joseph O’connor et Edmund Frederick Robertson de l’Université de St. Andrews au Royaume-Uni.
« Après neuf ans de travail dans le bureau, Thomas a arrêté d’obéir à son père en quittant son travail. Il est entré au Trinity College de Dublin, en Irlande, pour étudier les mathématiques, la philosophie, les classiques et les sciences afin d’obtenir un diplôme », expliquent les professeurs.
En 1835, Kirkman retourna en Angleterre et, quatre ans plus tard, devint vicaire d’une paroisse de l’Église anglicane, poste qu’il occupa pendant 52 ans. Il s’est marié et a eu trois enfants.
Comme l’a souligné Robin Wilson, professeur émérite de mathématiques à l’Open Université au Royaume-Uni, des propos publié dans The Early History of Block Designs, « Kirkman consacra peu de temps à ses fonctions paroissiales. »
Par conséquent, le révérend « consacra beaucoup d’efforts sur ses recherches mathématiques, en particulier sur les sujets d’algèbre et d’analyse combinatoire ».
Systèmes triples
En 1846, Kirkman présenta son premier article, publié en 1847 dans le Journal Cambridge and Dublin Mathematical Journal.
L’article est considéré comme le précurseur du système triple de Steiner, plusieurs années avant sa présentation par le géomètre suisse Jakob Steiner (1796-1863), considéré comme l’un des plus importants du 19ème siècle.

Crédit photo, Getty Images
« Peut-être que ces systèmes triples auraient dû être appelés systèmes Kirkman, puisqu’il a été le premier à les publier », a déclaré Ibáñez.
Tout au long de sa carrière, Kirkman s’est concentré sur la théorie des groupes et a laissé d’importantes contributions à l’analyse combinatoire.
Mathématiques récréatives
Kirkman a publié un travail de recherche relatif au problème des écolières dans The Lady’s and Gentleman’s Diary, consacré aux questions mathématiques, aux énigmes et à la poésie.

Crédit photo, Getty Images
C’était un puzzle, une énigme mathématique. Il est présenté de cette façon:
« Quinze jeunes écolières se promènent tous les jours de la semaine, du lundi au dimanche, de manière ordonnée, formant cinq rangées de trois écolières chacune. Comment devrions-nous les organiser tous les jours de la semaine pour qu’aucune paire d’écolières ne partagent la même file d’attente pendant plus d’une journée?
Cette approche a attiré l’attention de plusieurs mathématiciens reconnus, dont le Britannique Arthur Cayley (1821-1895), qui a rapidement publié une solution. Kirkman en présentera une autre et, à partir de ce moment-là, plusieurs résolutions émergeront.
Kirkman a fait ses débuts avec le problème des écolières exactement en écrivant son article sur les systèmes triples.
« Nous avons n éléments, 1, 2, 3 à n, et l’idée est de créer des collections de trois nombres dans cet ensemble, appelées blocs, de sorte que chaque paire d’éléments apparaisse exactement dans un trio », explique Ibáñez.
Ce que Kirkman demande dans son problème, c’est que pour 15 personnes ou éléments, nous pouvons développer un système triple séparé en sept groupes (un pour chaque jour de la semaine), de sorte que dans chacun d’eux trouvent tous les éléments - dans ce cas, le collégial.
Les carrés de la salle
Cayley est considéré comme l’un des pères fondateurs de l’école britannique de mathématiques pures, qui a émergé au 19ème siècle.
En 1850, il décida de se pencher sur le problème des 15 collèges et parvint à trouver une solution grâce à ce qui est maintenant connu sous le nom de carrés de salle – qui serait documenté par le mathématicien australien Thomas Gerald Room (1902-1986).
L’enseignant explique que dans un carré de salle, nous avons des symboles n+1.
Imaginez 8 chiffres, de 1 à 8.
Comme nous avons choisi huit symboles, nous faisons un tableau 7x7: sept lignes et sept colonnes.
Mais il est nécessaire de remplir trois conditions:
Chaque carré est vide ou possède une paire de chiffres. Par exemple, un carré peut en avoir 35, un autre peut avoir 86, un autre peut en avoir 13 ou rien.
Chaque symbole apparaît une fois dans chaque ligne et dans chaque colonne. Si nous prenons une ligne, par exemple, le 1 apparaîtra dans l’un des carrés, le 2 dans l’autre et ainsi de suite jusqu’au 8. Dans les colonnes, la même chose se produit, mais elles apparaîtront formant une paire de nombres.
Chaque paire de symboles non ordonnée n’apparaît qu’une seule fois. Le par 12, par exemple, apparaît une fois dans toute la table, le 13 n’apparaît qu’une seule fois, et donc jusqu’à la fin, jusqu’au par 78.
Voici un exemple :
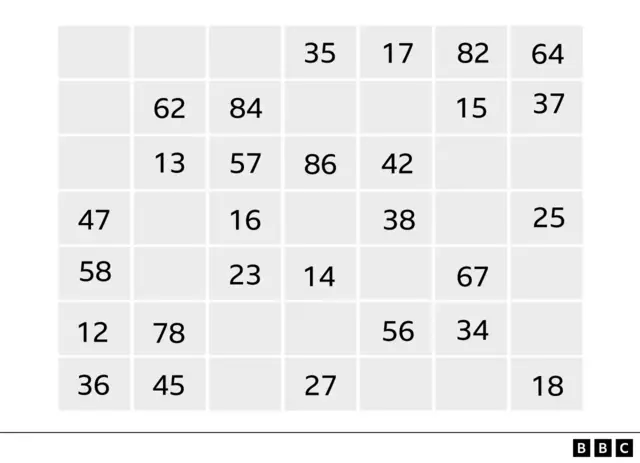
Crédit photo, Une autorisation de Raoul Ibanez
Ce que Cayley a fait, c’est utiliser ce genre de carré de salle et le combiner avec les systèmes triples, que Kirkman étudiait déjà, pour trouver une solution au problème collégial.
Cayley répartit les 15 élèves comme suit : il indiqua les sept premiers avec des lettres de « a » à « g », et les huit autres avec des chiffres, de 1 à 8.
Les nombres servent à former un carré de pièce, comme illustré ci-dessus, et les lettres à faire des systèmes triples d’ordre sept, comme ceci:

Crédit photo, Une autorisation de Raoul Ibanez
Ces trios sont placés à gauche de la place de la salle, comme suit:
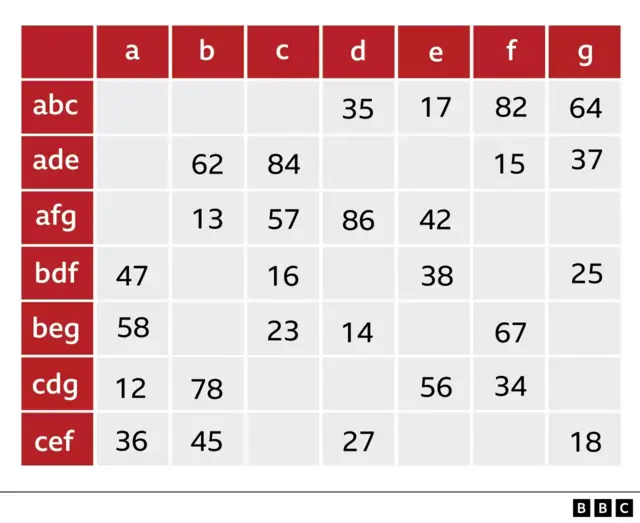
Crédit photo, Avec une autorisation de Raoul Ibanez
La solution
De cette structure, une solution surgit.
Transposons le tableau aux 15 lycéens et aux sept jours qu’ils vont se promener.
More d’abord, nommons les lettres et les numéros de table de Cayley:
a=Ana
b=Bia
c=Carol
d=Diana
e=Emma
f=Fany
g=Gina
1=Marie
2=Katy
3=Yeny
La solution vient du carré de lettres et de chiffres plus haut. Chaque rangée de cette place nous fournit des groupes de trois étudiants de chacun des sept jours de la semaine.C’est-à-dire que lundi est abc, d35, e17, f82 et g64. La solution, avec nos étudiants, serait la suivante :
L’art de l’analyse combinatoire
Kirkman et Cayley « savaient qu’il y avait quelque chose de profond derrière ce problème, alors ils ont tenté de le résoudre."

Crédit photo, Getty Images
« L’analyse combinatoire est l’art de sélectionner ou d’ordonner les éléments d’un certain ensemble » – et c’est précisément ce que Cayley nous montre avec sa solution. Le problème avec l’école secondaire, c’est l’organisation.
« Les élèves et la façon de les regrouper pour aller à l’école chaque jour sont une métaphore de la structure mathématique, en fait, combinatoire, qui peut être utilisée dans de nombreux autres aspects de notre vie », explique Ibáñez.
« C’est pourquoi les mathématiques sont abstraites – c’est donc un outil qui peut être utilisé dans des contextes très différents, tels que la physique, la biologie, la chimie ou la médecine. »
Selon lui, les mathématiques qui interviennent dans le problème des écolières font partie d’une branche entière qui est fondamentale dans la théorie du code et la cryptographie, la planification, la géométrie, les projets d’expériences statistiques, la théorie informatique et les réseaux de communication.
« Tout ce qui vient de la tentative de résoudre un puzzle a fini par devenir deux théories mathématiques: les systèmes triples de Steiner et la théorie de la conception de blocs, toutes deux avec de nombreuses applications pratiques », explique Ibáñez.
C’est parce que les mathématiques « ne se contentent pas » de résoudre le problème.
« Dans certains cas, comme celui-ci, il examine également le nombre de formes différentes de solutions. Et pour le problème de l’école Kirkman, il a été démontré au début du 20ème siècle qu’il y avait 80 solutions distinctes.
Le problème qui génère le plus de problèmes
Les écolières ont également soulevé de nouveaux problèmes.

Crédit photo, Getty Images
« Une autre pratique habituelle dans la science de Pythagore est d’exposer le problème plus généralement », explique Ibáñez.
« Par conséquent, le problème des écolières a été proposé pour les groupes avec d’autres quantités d’élèves. »
La solution pour tous les cas n’est venue qu’en 1968, lorsque les mathématiciens Ray-Chaudhuri et R. M. Wilson ont publié la « solution complète au cas général ».
Pourtant, le problème demeure, car les systèmes triples de Steiner ou, plus généralement, la conception par blocs sont une branche « très active » des mathématiques.
« Un puzzle comme celui-ci, qui en principe était une petite affaire, est devenu une théorie avec des centaines de problèmes ouverts, de recherches, d’articles et de livres », dit Ibáñez.
Et tout en essayant de le résoudre, de nombreux mathématiciens ont utilisé et développé différentes techniques.
Le mathématicien américain Martin Gardner, par exemple, a publié dans la revue Scientific American une solution géométrique au problème des écolières: un cercle, avec des nombres et des triangles dessus, qui offre une réponse différente lorsqu’il est tourné.
Pour en revenir à la question qui pourrait vous donner l’augmentation de salaire souhaitée, la réponse est de désigner un numéro pour chacun des invités et de créer un système triple, qui conduira, par exemple, à sept tables:
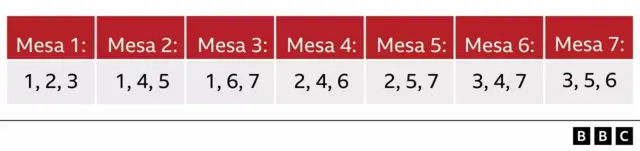
Crédit photo, Avec l'autorisation de Raoul Ibanez
Et si vous voulez remercier quelqu’un pour l’augmentation de salaire bien méritée, nul doute que les remerciements vont à Thomas Kirkman et, bien sûr, au professeur Ibáñez.