سرقت از لوور؛ آیا یک مسئله ریاضی ۵۰ ساله می‌توانست موزه را امن نگه دارد؟

در یک سرقت جسورانه از موزه لوور، دزدها توانستند در روشنایی روز جواهرات سلطنتی بی‌قیمتی را به سرقت ببرند. اما آیا یک مسئله هندسی قدیمی، که دهه‌ها از طرح آن می‌گذرد، می‌توانست به موزه‌ها در ارتقای امنیت‌شان کمک کند؟

فقط هشت دقیقه طول کشید. در این ۴۸۰ ثانیه، سارقان با استفاده از یک سکوی مکانیکی بالا رفتند تا به بالکنی در طبقه اول موزه لوور در پاریس برسند و سپس در روشنایی روز از طریق یک پنجره وارد شوند. آن‌ها پس از ورود، دو ویترین شیشه‌ای را شکستند و با هشت قطعه از جواهرات سلطنتی دوران ناپلئون فرار کردند. این یک «سرقت جسورانه» بود که فرانسه را به شدت تکان داد.

تا کنون چندین مظنون در ارتباط با این سرقت بازداشت شده‌اند. با این حال یکی از پرسش‌هایی که همچنان تحقیقات در مورد این سرقت را به چالش می‌کشد، این است که چرا سارقان زودتر شناسایی نشدند.

در جلسه‌ای در برابر سنای فرانسه بلافاصله پس از این سرقت، لورنس دکار، مدیر این موزه مشهور جهانی، اعتراف کرد که موزه در «حفاظت از جواهرات سلطنتی» شکست خورده است. او گفت بالکنی که سارقان از آن استفاده کردند، تنها یک دوربین داشت که، در جهت اشتباهی نصب شده بود و گزارشی مقدماتی نشان داد که در یک‌ سوم از اتاق‌های جناح دنون که محل سرقت بود، هیچ دوربین امنیتی‌ وجود نداشت. دکار به طور کلی اذعان کرد که کاهش نیروهای نظارت و امنیتی، موزه را آسیب‌پذیر کرده و تاکید کرد که باید سیستم امنیتی لوور تقویت شود تا بتواند «همه‌جا را پوشش دهد.»

وزارت فرهنگ فرانسه اعلام کرده که آژیرهای موزه همان‌طور که باید عمل کرده‌اند. با این حال، این سومین سرقت پرسر و صدا از موزه‌های فرانسه طی دو ماه اخیر است و این وزارتخانه را وادار کرده که برنامه‌های امنیتی جدیدی را در سراسر فرانسه اجرا کند.

در حالی که تردیدی نیست که امنیت موزه‌های امروزی پیچیده و پرهزینه است، یک مسئله ریاضی جالب ۵۰ ساله وجود دارد که مستقیما با همین موضوع سر و کار دارد.

این مسئله می‌پرسد: حداقل چند نگهبان یا معادل آن، دوربین مداربسته با دید ۳۶۰ درجه لازم است تا کل یک موزه تحت نظر قرار گیرد؟ این مسئله به عنوان «مسئله موزه» یا «مسئله گالری هنری» شناخته می‌شود. راه‌حل آن، راه‌حلی زیباست.

فرض می‌کنیم که تمام دیوارهای موزه خیالی ما خطوط صاف هستند، به‌طوری که نقشه کف ساختمان چیزی است که ریاضی‌دانان آن را چند ضلعی می‌نامند، شکلی با لبه‌ها و گوشه‌های مشخص.

دوربین‌ها باید در مکان‌های ثابتی قرار داشته باشند، اما می‌توانند در تمام جهات ببینند. برای اطمینان از اینکه کل موزه پوشش داده شده، باید بتوان از هر نقطه‌ای در نقشه کف، یک خط مستقیم به سمت حداقل یکی از دوربین‌ها رسم کرد.

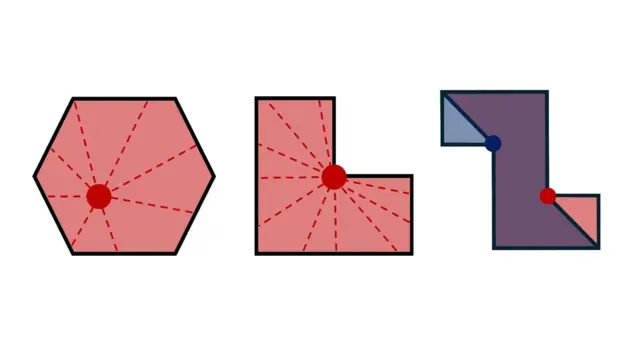
به گالری شش ‌ضلعی سمت چپ در نمودار زیر نگاهی بیندازید.

مهم نیست دوربین را کجا قرار دهید، می‌توانید کف و دیوارهای کل فضا را ببینید. وقتی از هر موقعیتی می‌توان همه جای گالری را دید، این شکل را چند ضلعی محدب می‌نامیم. گالری ال شکل وسط غیرمحدب است، به این معنا که در جای‌گذاری دوربین‌ها محدودیت داریم، اما باز هم می‌توان نقاطی یافت که یک دوربین از آن‌جا کل فضا را ببیند.

گالری زد شکل (سمت راست) به دو دوربین نیاز دارد. همیشه نقاطی هست که یک دوربین به تنهایی آن‌ها را پوشش نمی‌دهد.

برای نقشه‌های پیچیده‌تر (مثل نقشه غیرمعمول پانزده ‌ضلعی زیر) دانستن اینکه چند دوربین لازم است یا باید کجا قرار بگیرند بسیار سخت‌تر است. خوشبختانه برای مدیران موزه‌هایی با بودجه محدود، واسلاف شواتال، نظریه‌پرداز گراف، این مسئله را در قالبی کلی کمی پس از طرح آن در سال ۱۹۷۳ حل کرد.

پاسخ این است که تعداد دوربین‌ها بستگی به تعداد گوشه‌ها دارد (یا همان‌طور که ریاضی‌دانان می‌گویند: «رئوس»)، چرا که در یک اتاق، به تعداد گوشه‌ها دیوار داریم. یک تقسیم ساده به ما کمک می‌کند تعداد دوربین‌های لازم را مشخص کنیم.

با تقسیم تعداد گوشه‌های یک اتاق بر سه، می‌توان فهمید چند دوربین نیاز داریم. به شرطی که هر دوربین دید کامل ۳۶۰ درجه داشته باشد. این قانون حتی برای شکل‌های پیچیده‌ای مثل گالری عجیب پانزده ‌ضلعی زیر نیز کار می‌کند. در این مورد، پانزده گوشه داریم، پس پانزده تقسیم بر سه می‌شود پنج.

این روش حتی زمانی که تعداد گوشه‌ها به‌طور کامل بر سه بخش‌پذیر نباشد نیز جواب می‌دهد. مثلا برای گالری بیست ‌ضلعی، پاسخ می‌شود شش و دو سوم. در این موارد، می‌توان عدد صحیح را در نظر گرفت. بنابراین هیچ‌گاه به بیش از شش دوربین در یک اتاق بیست ‌ضلعی نیاز نداریم.

در سال ۱۹۷۸، استیو فیسک، استاد ریاضی در کالج بودین در ایالت مین آمریکا، برهانی برای این حد پایین تعداد دوربین‌های لازم ارائه کرد. برهانی که یکی از زیباترین برهان‌ها در تمام ریاضیات تلقی می‌شود.

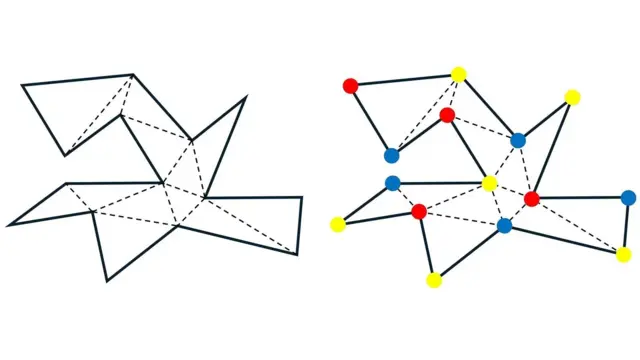
استراتژی او این بود که گالری را به مثلث‌هایی تقسیم کند (به تصویر سمت چپ در شکل زیر نگاه کنید). سپس او ثابت کرد که می‌توان فقط از سه رنگ مثلا قرمز، زرد و آبی استفاده کرد و برای هر گوشه از مثلث‌ها یک رنگ متفاوت اختصاص داد. به این ترتیب، هر مثلث در گالری گوشه‌هایی با سه رنگ متفاوت خواهد داشت (تصویر سمت راست شکل زیر را ببینید). این روش به عنوان «سه‌ رنگی» گوشه‌ها شناخته می‌شود.

مثلث‌ها از آن دسته چندضلعی‌های «محدب» هستند که پیش‌تر گفتیم، پس یک دوربین در هر گوشه (یا در واقع هر نقطه‌ای از مثلث) می‌تواند تمام نقاط آن را ببیند. هر مثلث سه رنگ دارد. یعنی می‌توان فقط یکی از رنگ‌ها را انتخاب کرد و دوربین‌ها را در همان موقعیت‌ها قرار داد. این دوربین‌ها قادر خواهند بود تمام بخش‌های هر مثلث و در نتیجه کل گالری را ببینند. اما نکته جالب‌تر اینجاست.

زیبایی برهان فیسک در این است که می‌توانید رنگی را انتخاب کنید که کمترین تعداد نقطه را دارد، و باز هم تمام گالری را پوشش می‌دهید. در شکل پانزده ‌ضلعی بالا، با انتخاب نقاط قرمز، می‌توان تنها با چهار دوربین کار را انجام داد.

در واقع، نقطه قرمز بالا سمت چپ ضروری نیست، چون دوربین قرمز بعدی می‌تواند کل فضای آن را پوشش دهد. بنابراین حتی با سه دوربین هم می‌توان این گالری را پوشش داد. این موضوع به‌ویژه زمانی صادق است که از دوربین‌های مدرن با دید همه‌جهات استفاده کنیم، نه دوربین‌های مدار بسته قدیمی با زاویه دید باز که باید فضا را جارو کنند و باعث ایجاد نقاط کور موقت می‌شوند.

اما باید به یاد داشت که بسیاری از موزه‌های سنتی مثل لوور، بیشتر اتاق‌هایی با شکل مستطیلی دارند. خوشبختانه، نسخه‌ای از مسئله گالری هنری وجود دارد که نشان می‌دهد وقتی دیوارها با زاویه ۹۰ درجه به هم می‌رسند، تنها یک دوربین برای پوشش کل اتاق کافی است.

دکار در شهادتش همچنین اذعان کرد که دوربین‌های پیرامونی لوور تمام دیوارهای خارجی ساختمان را پوشش نمی‌دهند. او گفت: «ما ورود سارقان را زود تشخیص ندادیم... ضعف در حفاظت پیرامونی ما شناخته ‌شده است.»

خوشبختانه، نسخه‌هایی از این مسئله وجود دارد با نام «مسئله قلعه» یا «مسئله زندان» که موضوع پوشش دوربین‌ها برای محیط خارجی ساختمان را نیز حل می‌کنند.

با این حال، هر دو نسخه نشان می‌دهند که یافتن نقاط دید مناسب، حیاتی است. اما مهم است بدانیم که سارقانی که به گالری‌های عمومی وارد می‌شوند، تنها تهدیدی نیستند که موزه‌ها با آن روبرو هستند. برای مثال، در موزه بریتانیا در لندن، در سال ۲۰۱۱ یک حلقه کارتیر به ارزش ۷۶۰ هزار پوند (۹۵۰ هزار دلار) از مجموعه‌ای که در معرض نمایش عمومی نبود، ناپدید شد.

جواهراتی از این موزه در سال ۲۰۲۰ در سایت ای‌بی برای فروش گذاشته شده بودند. گفته می‌شود این اقلام توسط یکی از متصدیان خود موزه برداشته شده بودند.

علاوه بر سرقت، موزه‌ها باید مجموعه‌های خود را در برابر خرابکاری، آتش‌سوزی و دیگر انواع تخریب نیز محافظت کنند.

با این حال، مسئله گالری هنری حتی برای کسانی خارج از تالارهای مقدس موزه‌ها ارزش توجه دارد. این مسئله در حوزه‌هایی که دید و پوشش کامل اهمیت دارد، کاربردهای فراوانی دارد.

برای مثال، در رباتیک به سیستم‌های خودران کمک می‌کند تا کارآمدتر شوند و از برخوردها جلوگیری کنند. در برنامه‌ریزی شهری، در تعیین محل آنتن‌های رادیویی، دکل‌های مخابراتی یا حسگرهای آلودگی برای پوشش جامع فضاهای عمومی کاربرد دارد.

در استراتژی‌های مدیریت بحران نیز از اصول مشابهی برای جای‌دهی پهپادها جهت بررسی مناطق فاجعه‌زده از هوا یا پیدا کردن ایستگاه‌های میدانی پزشکی استفاده می‌شود. در ویرایش تصویر و بینایی رایانه‌ای، مسئله گالری هنری می‌تواند در شناسایی نواحی قابل مشاهده در یک صحنه کمک کند. این مسئله حتی می‌تواند تضمین کند که بازیگران روی صحنه همیشه روشنایی کافی دارند و موزه‌ها بتوانند گالری‌های خود را به‌درستی نورپردازی کنند.

موزه لوور به پرسش‌های بی‌بی‌سی در مورد اینکه آیا از راه‌حل‌های ارائه‌شده در مسئله موزه آگاه است یا نه، پاسخی نداد. بی‌تردید این موزه در حال حاضر مسائل فوری‌تری برای رسیدگی دارد. اما همان‌طور که موزه‌ها و گالری‌های هنری در سراسر جهان در پی سرقت لوور بار دیگر نگاهی به امنیت خود می‌اندازند، یادآوری درس‌های این مسئله ریاضی ۵۰ ساله می‌تواند بی‌ضرر باشد.