Key points about percentage change

- An amount can be increased or decreased by a certain percentage to change its size.
- A reverse percentage problem involves finding the original amount before a percentage increase or decrease.
- The percentage increase or decrease between two numbers is called the percentage change. In situations that involve buying and selling, this may be called profit and loss.
Make sure you know how to calculate percentages of an amount and convert between fractions, decimals and percentages in order to understand percentage change.
Check your understanding
Video – Exam practice: Percentage changes
Watch this video to learn how to work out a new or an original value after a percentage increase or decrease.
How can learning percentage calculations in maths help you in everyday life?
Let's first look at how to calculate a new value if a percentage increase or decrease is applied to an original value.
Your favourite clothing store is having a 15% off sale. You spot a top originally priced at £50. How much will you pay after the discount?
There are a few different ways of working this out. We can either work out 15% and subtract this from the original price, £50, or we can work out 85% of the original £50 price to get the new sale price.
We find 85% because subtracting the 15% sale discount from 100% equals 85%. Here, we're going to work out the value of 85% of £50.
Without a calculator, you can find 85% of the original £50 by first working out what 10% is, which means we need to divide £50 by 10, since 10% is one tenth of 100%. 10% of 50 is 5.
Then, to calculate 80%, you multiply the 10% value, £5, by 8, which equals £40.
Then, to add a further 5% to find 85%, we work out half of the 10% value. This is £2.50.
So the new price after the 15% discount is £40 plus £2.50, which equals £42.50. You can use this method when you know the original price of something and need to calculate a new price.
Now, let's look at finding the original value of a number that's already had a percentage increase or decrease applied. Say a concert ticket costs £75 after a 25% increase. How much did it cost originally?
Here, we know the new price and the percentage by which it's been increased, and we need to calculate the original price. It's tempting to calculate 25% of £75 and subtract it, but that's not right.
The new price, £75, represents 125% of the original price. The original 100% plus the 25% increase in cost. To calculate the original value, the 100% cost, without a calculator, we first find a common factor that can divide both the new cost, £75, and the percentage it represents, 125%. In this case, 5 is a common factor. 125% divided by 5 is 25%, and £75 divided by 5 is £15.
This means that £15 is 25% of the value of the concert ticket. If we know £15 represents 25%, multiplying this by 4 will give us 100% of the original price. And £15 × 4 = £60. This means that the original price of the concert ticket was £60.
Remember, pay close attention to the key words in the question to make sure you choose the right method to answer it.
How to increase or decrease by a percentage
There are lots of instances where amounts are increased or decreased by a percentage, eg a box may contain 20% more cereal than usual, or a shop may have 15% off its prices.
There are two methods to increase or decrease by a percentage:
- Find the percentage of the amount and then add or subtract this from the original amount.
- Add or subtract the percentage from 100% and find this percentage of the amount.
Follow the working out below
GCSE exam-style questions

- A building company charges £2500 to fit a garage door.
Value Added Tax (VAT) Money that is added to the cost of goods or services that is then passed on to the government. is then added at 20%.
What is the cost with VAT ?
Work this out without a calculator.
The cost with VAT is £3000.
Value Added Tax (VAT) is money that is added to the cost of goods or services that is then passed on to the government.
- Find 20% of £2500.
- 10% of £2500 = £2500 ÷ 10 = £250
- 20% of £2500 = £250 × 2 = £500.
- Add £500 to the original amount.
- £2500 + £500 = £3000
- Cruz buys a phone for £280 and sells it for a 15% profit.
Carly buys a phone for £320 and sells it at a 5% loss.
Who sells their phone for the highest price?
Use the decimal multiplierA decimal that multiplies an amount. The decimal has usually been converted from a percentage. For example, in the calculation 80 × 0∙2, the multiplier is 0∙2. method on a calculator.
Cruz sold their phone for the most money.
- To find the selling price of Cruz’s phone, increase £280 by 15%.
100% + 15% = 115%.
Convert the percentage to a decimal multiplier:
115 ÷ 100 = 1·15.Find 115% of £280: 1·15 × £280 = £322.
- To find the selling price of Carly's phone, decrease £320 by 5%.
100% - 5% = 95%.
Convert the percentage to a decimal multiplier:
95 ÷ 100 = 0·95.Find 95% of £320:
0·95 × £320 = £304.
£322 is higher than £304, so Cruz sold their phone for more money.
- Elbie has completed 78% of a 2500-piece jigsaw.
How many pieces are left to put in place?
Use a calculator if needed.
550 pieces
Decrease 2500 by 78%:
- 100% - 78% = 22%, so there are 22% of the pieces left.
- Convert 22% to a decimal multiplier: 22 ÷ 100 = 0·22
- Find 22% of 2500: 0·22 × 2500 = 550 pieces.
Reverse percentages
Finding the original amount before a percentage increase or decrease has taken place is called a reverse percentage problem.
The original amount always represents 100%.
- If the original amount has increased by 5%, the new amount represents 105% of the original.
- If the original amount has decreased by 5%, the new amount represents 95% of the original.
There are two common methods to find the original amount (100%):
- Work out the amount that represents 1%, and then multiply by 100.
- Write and solve an equation involving a decimal multiplierA decimal that multiplies an amount. The decimal has usually been converted from a percentage. For example, in the calculation 80 × 0∙2, the multiplier is 0∙2..
Follow the working out below
GCSE exam-style questions

- A pair of trousers are shortened by 10%. They are now 72 cm long.
How long were they before they were shortened?
Work this out without a calculator.
80 cm
The original length is 100%.
The shortened length of 72 cm represents 90%.
- Divide by 9 to show that 8 cm represents 10%.
- Multiply by 10 to show that 80 cm represents 100%, so is the original length.
- A restaurant bill comes to £48 including a 20% service charge.
What was the bill before the service charge was added?
Work this out without a calculator.
£40
The bill before the charge was added represents 100%.
The bill after the charge is added represents 120%.
£48 represents 120%.
- Divide by 12 to find the value of 10%.
£4 represents 10%. - Multiply by 10 to find the value of 100%.
£40 represents 100%.
- A charity posted a video online on Saturday that received 4366 views.
This is 18% more than a video they posted on Friday.
How many views were received for their video on Friday?
Use a calculator if needed.
3700
The number of views on Friday’s video represents 100%.
The number of views on Saturday’s video is 18% more, so represents 118%.
- Let 𝑓 be the number of views on Friday’s video.
118% of 𝑓 = 4366 - Set up an equation using a decimal multiplier:
1·18𝑓 = 4366 - Solve by dividing both sides by 1.18:
𝑓 = 4366 ÷ 1·18 = 3700
Calculating the percentage change
Percentage change can be calculated by looking at the difference between two numbers and working out the percentage increase or percentage decrease between them.
Items are often bought for one price and then sold for another. The percentage change between the two prices shows the percentage profit or loss that has been made.
Percentage change is calculated by writing the actual change as a fraction of the original amount, and converting to a percentage.
To convert a fraction to a percentage, either use equivalent fractionA fraction with the same value as another. Each fraction represents the same proportion, eg ½ and ¹⁰⁄₂₀. to make the denominator 100, or multiply the fraction by 100.
As a formula:
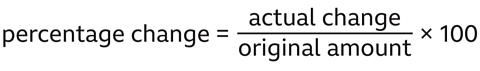
Follow the working out below
GCSE exam-style questions
- The results board shows the time it takes for an athlete to run 400 m in January and August.
What is their percentage improvement in time between the two months?
Work this out without a calculator.

5%
- Calculate the actual change in time:
60 – 57 = 3 seconds. - Write the actual change (3) over the original amount (60) to give \(\frac{3}{60}\).
- Divide the numerator and denominator of the fraction by 3.
This simplifies the fraction to \(\frac{1}{20}\), which is easier to convert to a percentage. - Convert \(\frac{1}{20}\) to a percentage. To do this, either:
- Write \(\frac{1}{20}\) as the equivalent fraction \(\frac{5}{100}\) = 5%
- Or convert \(\frac{1}{20}\) to the decimal 0·05 and multiply by 100.
The percentage improvement is 5%.
- Chloe buys a flat for £120,000.
She sells it for £165,000.
What is her percentage profit?
Use a calculator if needed.

37·5%
- Work out the actual change in price:
£165,000 – £120,000 = £45,000 - Substitute the actual change (45,000) and the original amount (120,000) into the formula for percentage change.
Percentage change = \(\frac{45,000}{120,000}\) × 100 - Use a calculator to obtain the answer of 37·5.
There is a percentage increase of 37·5%.
Quiz – Percentage change
Practise what you've learned about percentage change with this quiz. The questions change each time you try, so keep testing your knowledge.
Now you have revised percentage change, why not try this guide on Converting between fractions, decimals and percentages?
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Ratio, proportion and rates of change
Find out more by working through a topic
- count7 of 8

- count8 of 8