Key points about working with proportion
- Proportion is a relationship between two A quantity that can take on a range of values, eg, cost or weight. based on multiplication and division.
- The two types of proportion are A relationship between values where one value increases at the same rate as another, eg as one value doubles, the other value doubles. and A relationship between values where one value increases and the other decreases at the same rate, eg as one value doubles, the other value halves..
- To find the best value for money of similar goods, the A method that works out the value of one unit. Once the value of one unit is known, the value of any number of units can be calculated. can be used to find the cost per 1 unit.
Make sure you understand the idea of equivalent ratios, as the skills needed for work on proportion are very similar.
Check your understanding
Finding amounts using proportion
There are two types of proportional relationship that can exist between variables:
- When one value increases or decreases at the same rate as another, the two values are said to be directly proportional:
- If a weight is three times heavier in grams, it will be three times heavier in ounces.
- When one value increases and the other decreases at the same rate, the two values are said to be inversely proportional:
- If the speed of an object is doubled, the time it takes to travel a distance is halved.
Follow the working out below
GCSE exam-style questions
- Use 5 mph = 8 km/h to convert 72 km/h into mph.
45 mph
This is an example of direct proportion.
The speed in km/h has been multiplied by 9.
So, multiply the speed in mph by 9 also:
5 × 9 = 45 mph
- A person is paid £63.30 for 3 hours’ work.
How much are they paid for working 7 hours?
£147.70
This is direct proportion. Use the A method that works out the value of one unit. Once the value of one unit is known, the value of any number of units can be calculated.:
- Calculate the person’s pay for 1 hour:
£63.30 ÷ 3 = £21.10 - Calculate their pay for 7 hours:
£21.10 × 7 = £147.70
- A set of 6 machines can print 40 photos in 8 minutes.
How long would it take 4 machines to print 20 photos?
6 minutes
Use a table to record the given information, then change one thing at a time.
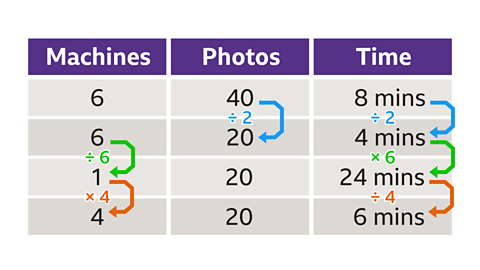
Find how long it would take for 6 machines to print 20 photos.
For the machines to print half as many photos (20), it would take half the time. This is direct proportion.- 6 machines, 20 photos, 4 minutes.
Find how long it would take for 1 machine to print 20 photos.
There are fewer machines, so it will take more time. This is inverse proportion. The machines have been divided by 6, so multiply the time by 6.- 1 machine, 20 photos, 24 minutes.
Find the time for 4 machines to print 20 photos.
There are more machines, so it will take less time. The machines have been multiplied by 4, so divide the time by 4.- 4 machines, 20 photos, 6 minutes.
Game - Direct and inverse proportion
Practise your direct and inverse proportion skills with these questions from our Divided Islands maths game.
Play the full Divided Islands game.
Best buy problems
The amount of a certain item and the total cost are A relationship between values where one value increases at the same rate as another, eg as one value doubles, the other value doubles. to each other.
If the amount of items is multiplied by 5, so is the cost. Similarly, if the amount of items is divided by 5, so is the cost.
When a shop offers different sizes of a product, proportion calculations can be used to decide which size gives the best value for money.
When making a comparison, either the cost or the size must be made the same. A A method that works out the value of one unit. Once the value of one unit is known, the value of any number of units can be calculated. can be used to work out the cost of a product per item, or per gram.
Follow the working out below
GCSE exam-style questions
- Which is better value for money:
5 cans for £3.50 or 4 cans for £2.60?
4 cans for £2.60 is better value.
Find the value of each can.
- For the first option, each can is:
3.50 ÷ 5 = £0.70 - For the second option, each can is:
2.60 ÷ 4 = £0.65
The second option is the best value for money, as it is cheaper per can.
- Shop A sells stickers at 40p each with a ‘buy 3 get 1 free’ offer.
Shop B sells stickers at 32p each.
Which shop is cheaper to buy 20 stickers?
Shop A is cheaper.
At Shop A, for every 3 stickers costing 40p, 1 is free.
15 stickers would be paid for, and 5 would be free.
The total cost is 40p × 15 = £6.00.At Shop B, the total cost is 32p × 20 = £6.40.
Quiz – Working with proportion
Practise what you've learned about working with proportion with this quiz.
Now you've revised working with proportion, why not try learning about multiples and factors?
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.
More on Ratio, proportion and rates of change
Find out more by working through a topic
- count8 of 8
- count3 of 8
