Equivalent fractions and decimals

Part ofMathsFractionsYear 5

Equivalent fractions and decimals

There are two children sitting at a table. One of them is thinking with a thought bubble above while the other writes on a piece of paper. Within the thought bubble is the equation 0.1 = one tenth.

Fractions and decimals are linked. They are both ways of representing parts of a whole.

Even though they look different, fractions can have the same value as decimals and decimals can have the same value as fractions.

These are called equivalent fractions and decimals.

Sometimes it is better to present the answer to calculations in decimals, and sometimes it is better in fractions.

There are two children sitting at a table. One of them is thinking with a thought bubble above while the other writes on a piece of paper. Within the thought bubble is the equation 0.1 = one tenth.
Back to top

Activity: Equivalent fractions and decimals

Complete this interactive activity to understand equivalent fractions and decimals. Then put your knowledge to the test.

Back to top

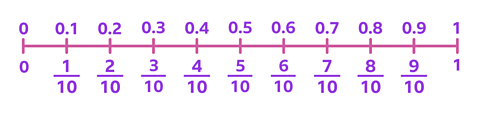
Tenths

0.1 is the same as \(\frac {1} {10}\)

This number line shows that \(\frac {1} {10}\) and 0.1 are equivalent. They have the same value, even though they look different.

A number line between 0 and 1. Above, the number line increases in decimal increments as 0.1. Below, the number line increases in faction increments of one tenth.

When finding fractions of a whole that is not divided into 10, such as \(\frac {1} {2}\), you can use a 100 grid.

This grid has been divided in half. There are 5 tens in each half, so \(\frac {1} {2}\) is the same as \(\frac {5} {10}\) and the same as 0.5.

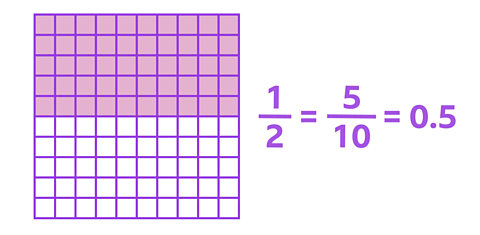
A 100 square grid with half of the squares shaded. Beside the grid there is an equation showing that the fraction one half is equivalent to five tenths and equivalent to 0.5.
Back to top

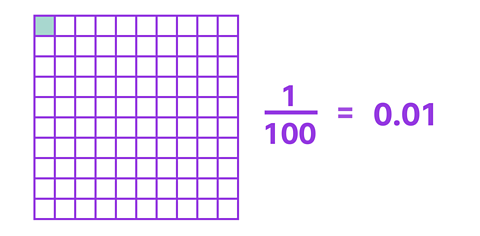
Hundredths

This one hundred grid is a whole that has been divided into one hundred squares.

As a decimal, \(\frac {1} {100}\) is written as 0.01.

A one hundred square grid with one square shaded. Beside the grid on the left is the fraction one hundredth. Beside the grid on the right is the decimal 0.01.

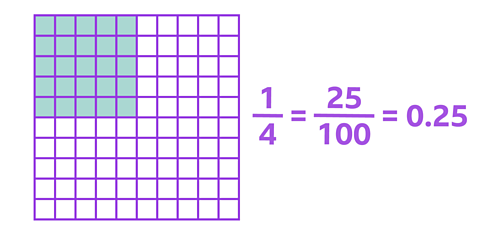
In the following grid 25 squares have been shaded:

That's twenty five hundredths, or two tenths and five hundredths.

As a fraction is it written as \(\frac {25} {100}\).

As a decimal, it is written as 0.25.

\(\frac {25} {100}\) is also equivalent to \(\frac {1} {4}\), so \(\frac {1} {4}\) is equivalent to 0.25.

A one hundred square grid with 25 squares shaded. To the side there is an equation that shows that the fraction one quarter is equivalent to the fraction twenty five hundredths, which is also equivalent to the decimal 0.25.
Back to top

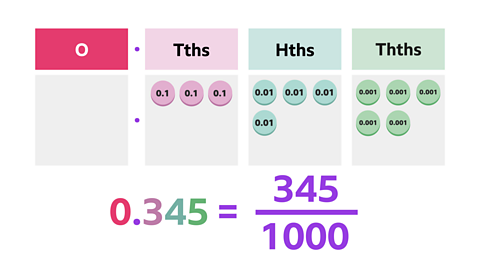
Thousandths

Each square in this one hundred grid is divided into tens.

A 1000 square grid.

Now the whole has been divided into thousandths.

As a decimal, \(\frac {1} {1000}\) is written as as 0.001.

A zoomed in version of the 100 grid. Each square contains 10 further squares making the grid a 1000 grid. One of the inner squares is shaded. To the left of this grid is the fraction one thousandth with the decimal 0.001 below it.

In the next image, the shaded part represents \(\frac {8} {1000}\) in fractions and 0.008 in decimals.

A zoomed in version of the 100 grid. Each square contains 10 further squares making the grid a 1000 grid. eight of the inner squares is shaded. To the left of this grid is the fraction eight thousandths with the decimal 0.008 below it.

Place value tables and counters can help when working with thousandths.

Skip image gallery
  1. A place table. There are 4 headings 'ones', 'tenths', 'hundredths' and 'thousandths' with a decimal point separating the 'ones' from the rest. Within the 'tenths' column there are three 0.1 counters. Within the 'hundredths' column there are four '0.01' counters. Within the 'thousandths' column there are five 0.001 counters. Underneath the place value table the decimal 0.345 is present.
Back to top

Example 1

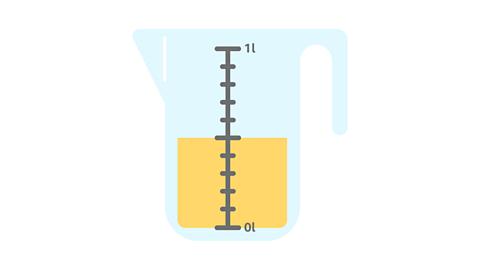
A measuring jug half full of liquid.

Here is a jug that is half full.

How can you represent this in fractions and decimals?

Back to top

Example 2

There are two fractions, one fifth and one quarter. There are two decimals, 0.25 and 0.5.

Put these decimals and fractions in order, from smallest to largest.

\(\frac {1} {5}\), \(\frac {1} {4}\), 0.5, 0.25

You may need to convert them into equivalent fractions or decimals. Some of the fractions and decimals may have the same value.

Back to top

Example 3

A place table. There are 4 headings 'ones', 'tenths', 'hundredths' and 'thousandths' with a decimal point separating the 'ones' from the rest. Within the 'tenths' column there are four 0.1 counters. Within the 'hundredths' column there are five '0.01' counters. Within the 'thousandths' column there are five 0.001 counters.

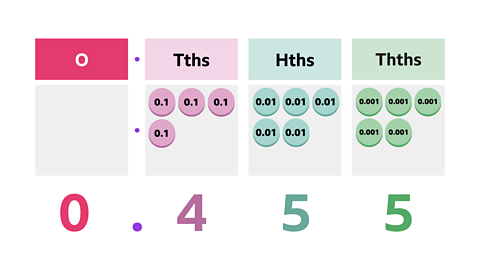
What decimal number is represented by the place value counters?

Can you also represent it using a fraction?

Back to top

More on Fractions

Find out more by working through a topic