Adding and subtracting fractions
When adding or subtracting fractions, you need to look at the denominator.
If the denominator is the same, then you can just add or subtract the numerator.
If the denominator is different, then you need to find an equivalent fraction that makes both numbers the same.
Activity: Adding and subtracting fractions with different denominators
Complete this activity to learn how to add and subtract fractions with different denominators and then put your knowledge to the test with a quiz.
Adding fractions with different denominators
When the denominators are the same you can just add the numerators.
For example:
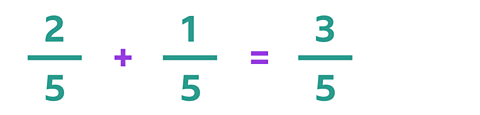
When you're adding and subtracting fractions with different denominators, you need to change one, and sometimes both, of the fractions so that they have the same denominator.
Let's look at an example:
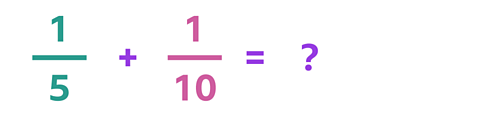
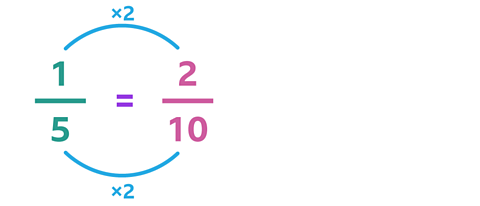
Here you can change the fraction \(\frac{1}{5}\) to \(\frac{2}{10}\) by multiplying the numerator and the denominator by 2.
Now you can add the fractions because they have the same denominator.
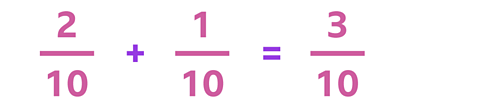
Subtracting fractions with different denominators
Now let's try subtracting fractions with different denominators.
Here you need to change both fractions.
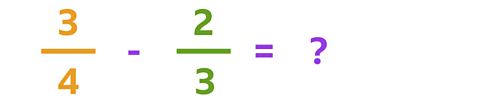
You need a number that is a multiple of 3 and 4.
The lowest common multiple of these numbers is 12.
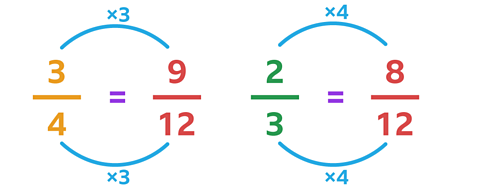
You can convert \(\frac{3}{4}\) to \(\frac{9}{12}\) by multiplying the numerator and denominator by 3.
You can convert \(\frac{2}{3}\) to \(\frac{8}{12}\) by multiplying the numerator and denominator by 4.
Now you can do the calculation as the two fractions have the same denominator.
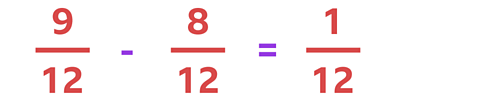
Example 1
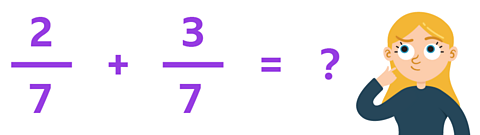
These fractions have the same denominator.
Can you find the answer?
✓ As the fractions have the same denominator, you only need to add the numerators together.
The answer is \(\frac{5}{7}\).
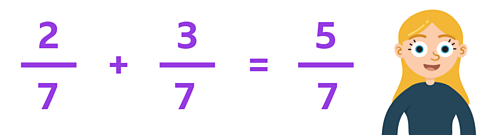
Example 2
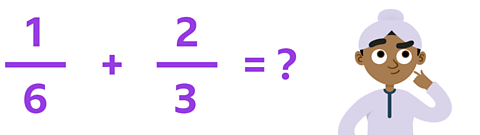
If both denominators are different, what do you need to do?
✓ You need to change the fraction \(\frac{2}{3}\) so that it has 6 as its denominator.
To do this multiply the denominator by 2. To make sure that the value of the fraction isn't changed, remember to multiply the numerator by 2 as well.
This gives you the fraction \(\frac{4}{6}\).
You can then do the addition calculation. The answer is \(\frac{5}{6}\).
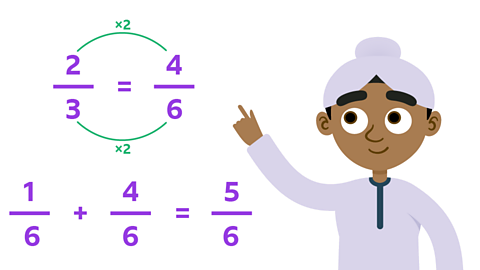
Example 3
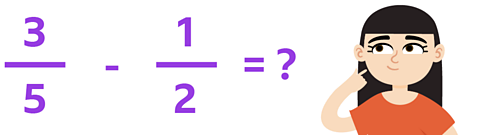
What's the lowest common multiple you can use, to help find the answer to this subtraction calculation?
✓ To find the new denominator, you're looking for a number that's a multiple of 2 and of 5.
The smallest number that's a multiple of both 2 and 5 is 10.
You need to change both fractions so that they have the same denominator.
To convert \(\frac{3}{5}\), multiply the numerator and the denominator by 2. You end up with \(\frac{6}{10}\).
To convert \(\frac{1}{2}\), multiply the numerator and the denominator by 5. You end up with \(\frac{5}{10}\).
You can now do the subtraction calculation. The answer is \(\frac{1}{10}\).
Play our fun maths game Guardians: Defenders of Mathematica. game
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica
More on Fractions
Find out more by working through a topic
- count15 of 17
- count16 of 17
- count17 of 17
- count1 of 17
