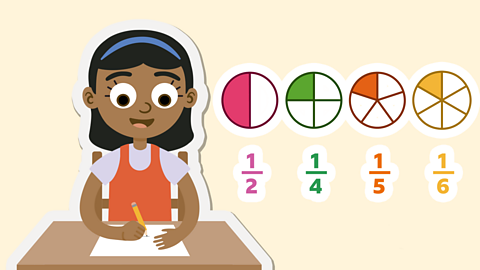
Multiplying fractions
When you multiply numbers together, you’re looking at how many groups of, or lots of, something you have.
You can use this same thinking, when you are multiplying fractions. For example:
\( \frac{2}{3} \) × 3 = ?
You can think about this as 3 lots of \( \frac{2}{3} \), or 3 group of \( \frac{2}{3} \), which is 2.
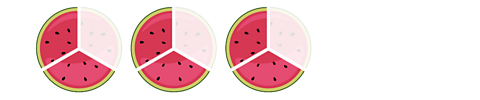
Therefore:
\( \frac{2}{3} \) × 3 = 2
You can multiply fractions by whole integers, or multiply fractions together.
Activity: How to multiply fractions
Complete this interactive activity to learn more about multiplying fractions and then put your knowledge to the test with a quiz.
How to multiply fractions
When multiplying fractions, you're looking at how many groups of, or lots of, something you have.
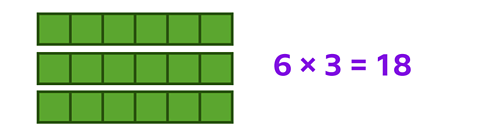
Look at this calculation:
6 × 3 = ?
You are looking for 3 groups of 6, which is 18.
Now, look at this calculation:
6 × \( \frac{1}{2} \) = ?
You are looking for a half group of 6, which is 3.

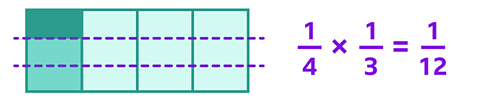
Sometimes you need to multiply a fraction by another fraction.
\( \frac{1}{4} \) × \( \frac{1}{3} \) = ?
You need to find \( \frac{1}{3} \) of a group of \( \frac{1}{4} \), which is \( \frac{1}{12} \).
You can also find the answer to a calculation using only the fraction symbols.
In this calculation, you are looking for \( \frac{2}{3} \) of a group of \( \frac{5}{6} \):
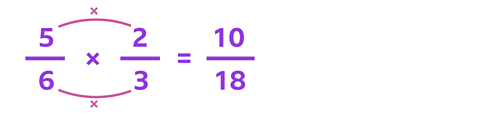
When you multiply two fractions, you multiply the denominators.
6 multiplied by 3 gives you the new denominator of 18, or eighteenths.
Then multiply the numerators together, to find out how many of these parts there are.
5 multiplied by 2 gives you the new numerator of 10.
So the answer is \( \frac{10}{18} \).
Example 1

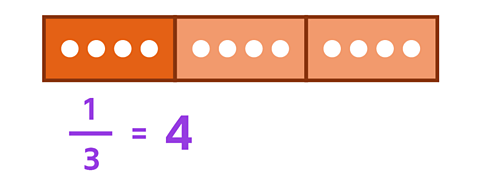
If you have \(\frac{1}{3}\) of a group of 12, how many do you have?
✓ Splitting 12 into 3, is the same as saying that you have \(\frac{1}{3}\) of a group of 12. So:
12 × \(\frac{1}{3}\) = 4
Example 2
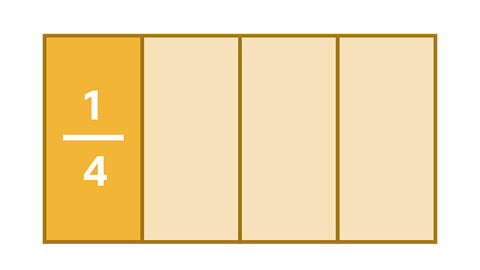
Solve this calculation:
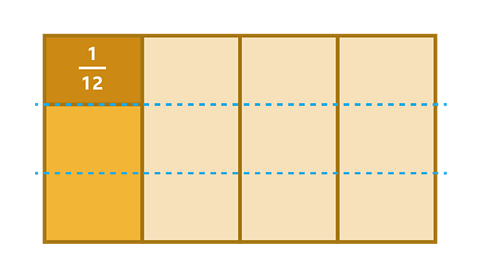
\(\frac{1}{4}\) × \(\frac{1}{3}\) = ?
✓ This is the same as saying that you have \(\frac{1}{3}\) of a group of \(\frac{1}{4}\), which is \(\frac{1}{12}\).
\(\frac{1}{4}\) ×\(\frac{1}{3}\) = \(\frac{1}{12}\)
Example 3
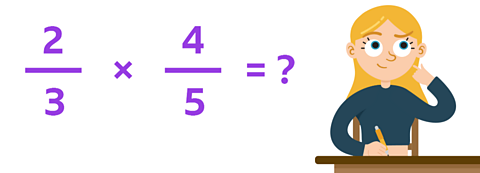
Which numbers do you multiply to work out \(\frac{2}{3}\) x \(\frac{4}{5}\)?
✓ First you multiply the denominators together, to find out what thirds of a fifth are. This gives you a new denominator of 15.
Next, multiply the numerators together to find out how many parts there are. This gives you a new numerator of 8.
\(\frac{2}{3}\) × \(\frac{4}{5}\) = \(\frac{8}{15}\)
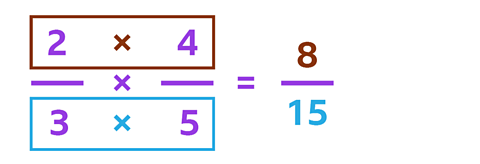
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Fractions
Find out more by working through a topic
- count16 of 17

- count17 of 17

- count1 of 17

- count2 of 17