Ordering fractions

Fractions can be ordered, just like whole numbers.
These rules can help you order fractions.
When ordering unit fractions:
- if the whole is the same, then the smaller the number of equal parts, the bigger each equal part is
This means that, with unit fractions, the greater the denominator, the smaller the fraction.
When ordering fractions with the same denominator:
- the greater the numerator, the larger the fraction is.

Activity: Ordering fractions
Complete this interactive activity to understand how to order fractions, then put your knowledge to the test.
Comparing fractions of a whole
A fraction shows you how many equal parts of one whole you have. So in order to compare fractions, the whole needs to be the same.
Look at these two circles.
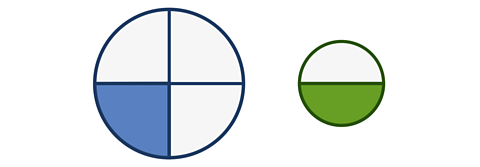
\(\frac {1} {4}\) of the blue circle is larger than \(\frac {1} {2}\) of the green circle.
But this doesn't mean that \(\frac {1} {4}\) is larger than \(\frac {1} {2}\) because the two circles, or wholes, are not the same size.
As one circle is bigger than the other, you cannot compare the two fractions, just the size of the shapes.
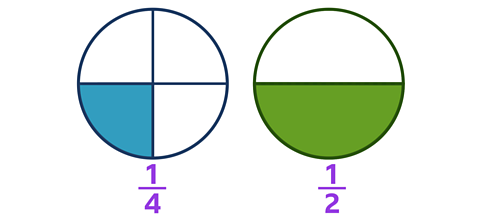
When the circles are the same size, you can see that \(\frac {1} {4}\) is smaller than \(\frac {1} {2}\).
Ordering unit fractions
In unit fractions, the numerator is always 1.
In this bar model, the whole is the same amount, but each bar has been divided into a different number of parts. This means the denominators are different.
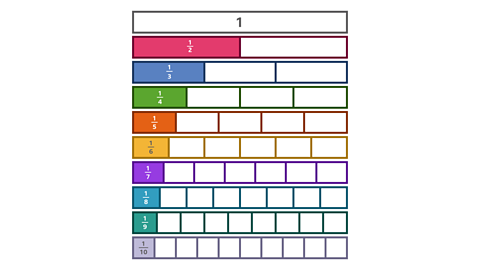
Each bar represents a different unit fraction.
The unit fractions in this model have been ordered. You can see that the higher the denominator is, the smaller the fraction is.
Ordering fractions with the same denominator
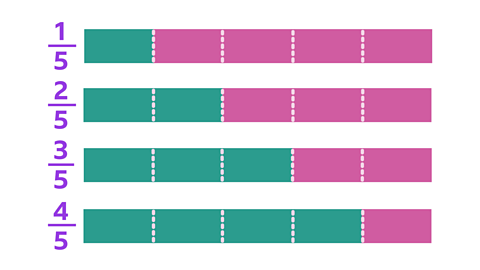
When fractions have the same denominator, you only need to look at the numerator to order the fractions.
The fraction is larger when the numerator is a bigger number.
This is because you are looking at more parts of the whole.
Example 1
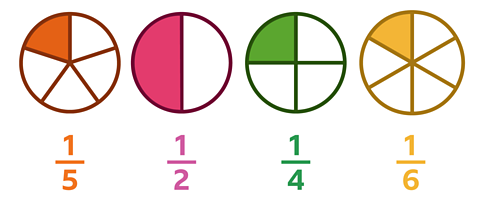
Order these unit fractions from largest to smallest.
✓ The correct answer is:
\(\frac {1} {2}\), \(\frac {1} {4}\), \(\frac {1} {5}\), \(\frac {1} {6}\)
Remember, when ordering unit fractions, the greater the denominator is, the smaller the fraction will be.
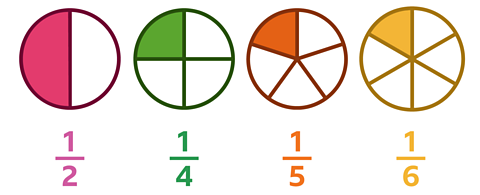
Example 2
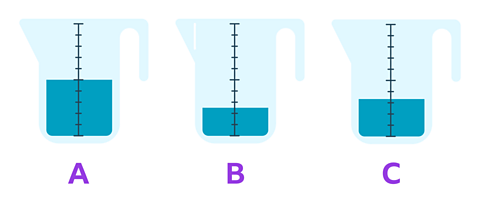
Use unit fractions to describe how full these containers are.
✓ Here are the answers:
A is \(\frac {1} {2}\) full
B is \(\frac {1} {4}\) full
C is \(\frac {1} {3}\) full
\(\frac {1} {2}\) is the most full and \(\frac {1} {4}\) is the least full.
In order from largest to smallest, these fractions are:
\(\frac {1} {2}\), \(\frac {1} {3}\), \(\frac {1} {4}\)
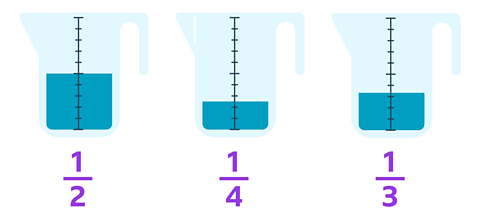
Example 3
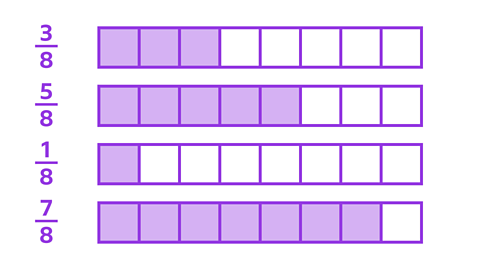
Order these fractions with the same denominators from smallest to largest.
✓The correct answer is:
\(\frac {1} {8}\), \(\frac {3} {8}\), \(\frac {5} {8}\), \(\frac {7} {8}\)
Remember, when ordering fractions with the same denominators, the larger the numerator, the larger the fraction.
Look at how many parts are shaded in each circle to help you decide.
More on Fractions
Find out more by working through a topic
- count3 of 17

- count4 of 17

- count5 of 17
- count6 of 17
