Comparing unit fractions
Unit fractions can be compared by looking at the denominator, or the number of equal pieces the whole has been divided into.
The denominator is the number below the division bar.
Unit fractions always have the number 1 above the division bar.
This is an example of a unit fraction:

Fractions with a numerator higher than 1 can also be compared.
Comparing fractions with the same denominator is much easier than comparing fractions with different denominators.
When you compare fractions with the same denominator look at the numerators (the numbers above the division bars). The larger the numerator is, the larger the fraction is.
Activity: How to compare fractions
Complete this interactive activity to understand how to compare fractions. Then put your knowledge to the test.
How to compare unit fractions
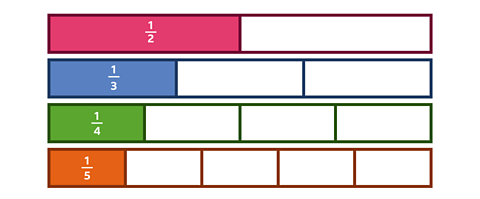
Bar models can help you to compare unit fractions.
Look at this bar model.
Each bar represents a whole. They are both the same size, but they have been divided into a different number of equal parts.
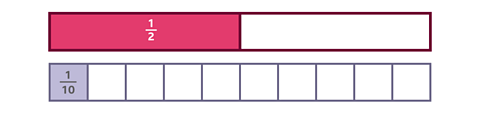
You can see by looking at the bars that \(\frac {1} {10}\) is smaller than \(\frac {1} {2}\).
The greater the number of equal parts, the smaller each equal part is.
As this bar model shows, comparing unit fractions by looking at the denominator involves thinking in the opposite way to when you compare whole numbers.
As the denominator gets higher, the fraction becomes smaller.
How to compare fractions with the same denominator
When you compare fractions with the same denominator, you only have to focus on the numerator.
Here is a circle. It has been split into four equal parts. Each part is one quarter.
Look at the fractions when each part is shaded. Which fraction is the biggest?
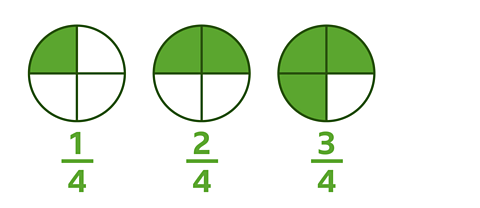
The fraction is larger if the numerator is a bigger number.
So, \(\frac {3} {4}\) is the biggest.
Example 1
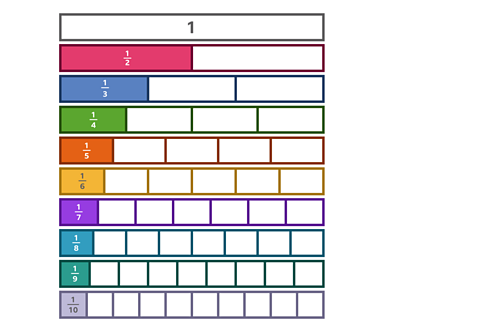
Which fractions are larger than \(\frac {1} {5}\)?
You can use the bar models to help you.
✓ \(\frac {1} {2}\), \(\frac {1} {3}\) and \(\frac {1} {4}\) are larger than \(\frac {1} {5}\).
Remember, when comparing unit fractions, as the denominator gets higher, the fraction becomes smaller.
Example 2
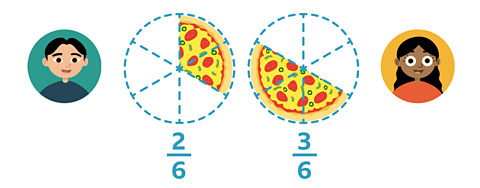
James and Maya cut a pizza into 6 slices. James ate \(\frac {2} {6}\) of the pizza and Maya ate \(\frac {3} {6}\).
Who ate more pizza?
✓ Maya ate more of the pizza.
Look at the fractions \(\frac {3} {6}\) and \(\frac {2} {6}\).
Which has the larger numerator?
The fraction \(\frac {3} {6}\) has the larger numerator, so Maya ate more of the pizza.
\(\frac {3} {6}\) > \(\frac {2} {6}\)
Remember, when fractions have the same denominator, the larger the numerator is, the larger the fraction is.
More on Fractions
Find out more by working through a topic
- count5 of 17
- count6 of 17

- count7 of 17

- count8 of 17
