What is a fraction of an amount?
A fraction is part of a whole. When you find a fraction of an amount, you work out how much that part is worth, compared to the whole.
Here is a quarter written as a fraction.

The numerator is 1 and the denominator is 4. You need to know these values to help you calculate a fraction of an amount.
You can see fractions of amounts all around you.
Shops have sales that say "\(\frac{1}{2}\) price" or "\(\frac{2}{3}\) off".
You might use fractions when baking, for example, “add half a teaspoon of salt” or “use a \(\frac{1}{4}\) of a kilogram of flour”.
Quiz
Why not see how much you know about this topic already? Then complete the guide and see if you can beat your score.
Finding fractions with a bar model
A bar model is helpful for finding fractions of amounts.
Let's use a bar model to find \(\frac{2}{5}\) of 20.
First you need to label the whole.

Next, divide one of the bars into fifths – five equal parts.
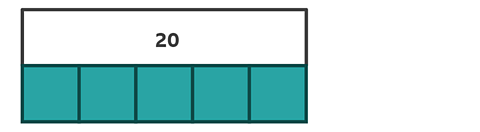
The bar model shows us that you need to divide 20 by 5. You can use dots to share out the 20 between each fifth.
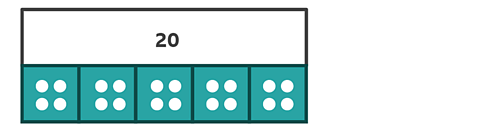
You need to look at two of the sections because you're looking for two fifths.
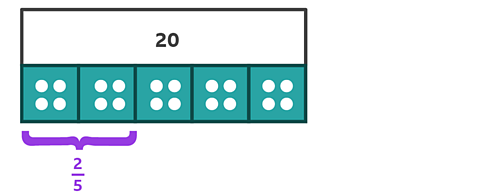
\(\frac{2}{5} \) is two of the parts in the bar model because each part represents \(\frac{1}{5}\).
They can be any two parts since they are all equal.
If \(\frac{1}{5}\) equals 4, then \(\frac{2}{5}\) equals 8. So:
\(\frac{2}{5}\) of 20 = 8
Finding fractions with a bar model
Let's try another one.
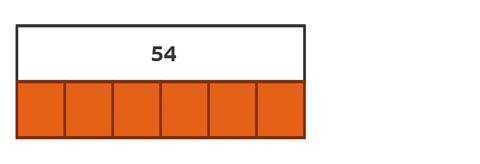
This time let's find \(\frac{4}{6} \) of 54.
First you need to label the whole.

Divide the bottom bar into 6 equal parts, because you are finding sixths.
Next, you find \(\frac{1}{6}\). You can use your times table facts to help you.
6 × ? = 54
Or you can use your division tables facts.
54 ÷ 6 = ?
54 ÷ 6 = 9
Therefore each sixth is worth 9.
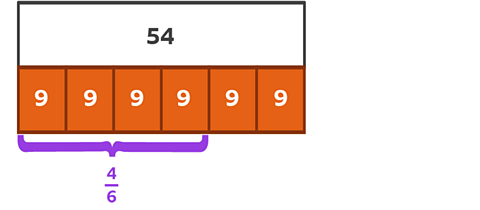
You need to find \(\frac{4}{6}\) so you find the total of four parts.
9 × 4 = 36
Therefore:
\(\frac{4}{6}\) of 54 = 36
Finding fractions of amounts
You may have noticed that you are following rules when you are using a bar model.
Once you know the rules, you may not need to have a visual to help you.
Rule 1 - Divide by the denominator
Rule 2 - Multiply by the numerator
Let’s try one without using a bar model.
Let's find \(\frac{7}{9}\) of 72.
First, you divide the whole amount by the denominator to find \(\frac{1}{9} \).
72 ÷ 9 = 8
\(\frac{1}{9}\) = 8
Then you multiply this by the numerator. You do this because you have only found \(\frac{1}{9} \).
In this question you need to find \(\frac{7}{9}\) so you multiply by 7.
8 × 7 = 56
\(\frac{7}{9}\) of 72 = 56
Example 1

Find \(\frac{2}{3} \) of 24.
✓ First, label the whole and then divide one of the bars into thirds – three equal parts.
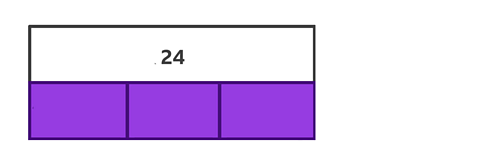
The bar model shows you that you need to divide 24 by 3.
Share out 24 dots between each third.
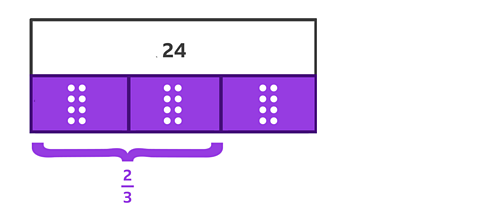
\(\frac{2}{3} \) is two of the parts in the bar model, because each part represents \(\frac{1}{3} \).
\(\frac{1}{3} \) equals 8, then \(\frac{2}{3} \) equals 16.
\(\frac{2}{3} \) of 24 = 16
Example 2

Find \( \frac{4}{5} \) of 55.
✓First, label the whole and then divide the bottom bar into 5 equal parts because you are finding fifths.
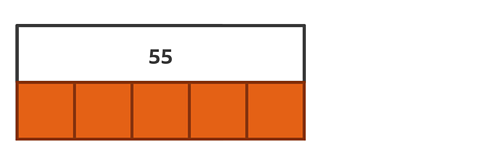
Next, you need to find \(\frac{1}{5} \).
You can use your times table facts to help you.
5 × ? = 55
Or you can use your division tables facts.
55 ÷ 5 = ?
55 ÷ 5 = 11,
Therefore each fifth is worth 11.
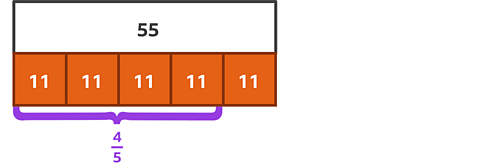
You need to find \(\frac{4}{5} \) so you find the total of four parts.
If \(\frac{1}{5} \) equals 11, then \(\frac{4}{5} \) equals 44.
11 × 4 = 44
\(\frac{4}{5} \) of 55 = 44
Example 3
Find \(\frac{9}{12}\) of 36.
✓ Let's answer this one without a bar model.
First, divide the whole amount by the denominator:
36 ÷ 12 = 3
\(\frac{1}{12} \) = 3
Then you multiply this by the numerator. You do this because you have only found \(\frac{1}{12} \).
In this question you need to find \(\frac{9}{12} \) so you multiply by 9.
3 × 9 = 27
\(\frac{9}{12} \) of 36 = 27
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Fractions
Find out more by working through a topic
- count7 of 17

- count8 of 17

- count9 of 17

- count10 of 17
