What are unit, non-unit and mixed fractions?

A unit fraction is any fraction where the numerator is 1, for example \(\frac{1}{4}\).
A non-unit fraction is a fraction where the numerator is not 1, for example \(\frac{4}{5}\).
Mixed fractions are a mix of whole numbers and a fraction together, for example 1 \(\frac{1}{4}\).
Sometimes you need to change how fractions are written to make them more useful.

Activity: Unit, non-unit and mixed fractions
Complete this interactive activity to learn how to understand unit, non-unit and mixed fractions. Then put your knowledge to the test.
Converting between top heavy fractions and mixed numbers
Take a look at the slideshow below to recap unit fractions, non-unit fractions and mixed numbers.

Image caption, A unit fraction always has the numerator 1.

Image caption, In a non-unit fraction, the numerator is any number other than 1.

Image caption, In a top heavy fraction, the numerator is larger than the denominator.
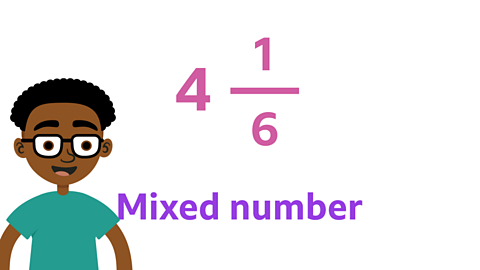
Image caption, In a mixed number, there are whole numbers and fractions together.
1 of 4
To change a top heavy fraction into a mixed number, work out how many wholes you can make and then add on the remaining parts.
So if you have \(\frac{5}{4}\), you can make 1 whole part of \(\frac{4}{4}\) and you have \(\frac{1}{4}\) remaining.
This means that \(\frac{5}{4}\) is the same as 1 \(\frac{1}{4}\).
To change a mixed number into a top heavy fraction, change the whole numbers into fractions and then add up how many parts you have in total.
If you have 2 \(\frac{1}{3}\), each of the whole numbers becomes \(\frac{3}{3}\), so here you have:
\(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{1}{3}\) = \(\frac{7}{3}\)
This means 2 \(\frac{1}{3}\) as a top heavy fraction is \(\frac{7}{3}\).
Example 1

Is \(\frac{5}{6}\) a unit or non-unit fraction?
✓ \(\frac{5}{6}\) is a non-unit fraction as the numerator is not one.

Example 2

Is \(\frac{6}{4}\) bigger than 1?
✓ \(\frac{6}{4}\) is bigger than 1.
There are 4 slices in each pizza. Each slice represents one quarter.
If you eat 4 of these quarters of pizza you have eaten \(\frac{4}{4}\), or a whole pizza.
So \(\frac{6}{4}\) is bigger than one whole.

Example 3

Is \(\frac{8}{3}\) the same as 2 \(\frac{1}{3}\)?
✓ \(\frac{8}{3}\) is not the same as 2 \(\frac{1}{3}\).
If a whole pizza is 3 slices, you can make 2 whole pizzas with 2 slices left.
This means that you have 2 whole pizzas and \(\frac{2}{3}\), which is not the same as 2 \(\frac{1}{3}\).

Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Fractions
Find out more by working through a topic
- count10 of 17

- count11 of 17

- count12 of 17

- count13 of 17
