Finding equivalent decimals and fractions
Fractions and decimals are both ways of representing parts of a whole.
Even though they look different, a fraction can have the same value as a decimal and a decimal can have the same value as a fraction.
These are called equivalent fractions and equivalent decimals.
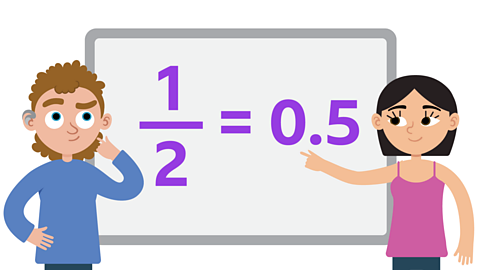
To find equivalent decimals for halves and quarters, you can use division or remember some common conversions:
\(\frac {1} {2}\) = 0.5
\(\frac {1} {4}\) = 0.25
\(\frac {3} {4}\) = 0.75
Quiz: Equivalent decimals of halves and quarters
Test out your knowledge of equivalent decimals of halves and quarters with this quiz, then read on to complete the page.
One half as a decimal
The equivalent decimal of \(\frac {1} {2}\) is 0.5.
Let's explore why…
Take a look at these squares. Each one has been divided into a different number of parts, but one half of the overall square has been shaded.
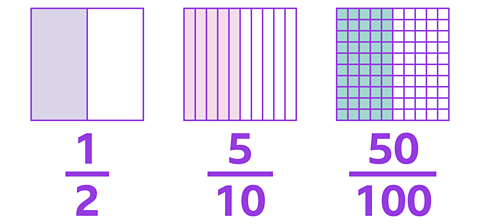
\(\frac {1} {2}\) shows that 1 part out of 2 is shaded.
\(\frac {5} {10}\) shows that 5 parts out of 10 are shaded.
\(\frac {50} {100}\) shows that 50 parts out of 100 are shaded.
You can say that:
\(\frac {1} {2}\) = \(\frac {5} {10}\) = \(\frac {50} {100}\)
They are all equivalent fractions.
Now, let's take a look at how you can find the decimal equivalent of these fractions by using place value counters.
This is how \(\frac {5} {10}\) can be represented using place value counters:

The fraction \(\frac {1} {10}\) is one tenth and it is written as 0.1 in decimals.
So, this is how the fraction \(\frac {5} {10}\) can be represented using five 0.1 decimal counters:

When added together, the counters make the decimal 0.5.
As \(\frac {5} {10}\) is equivalent to 0.5, then \(\frac {1} {2}\) and \(\frac {50} {100}\) must also be equal to 0.5, as each of those fractions are equivalent.
\(\frac {1} {2}\) = \(\frac {5} {10}\) = \(\frac {50} {100}\) = 0.5
This means the decimal equivalent of \(\frac {1} {2}\) is 0.5.
One quarter as a decimal
The equivalent decimal of \(\frac {1} {4}\) is 0.25.
Let's explore why…
In each of the representations below, one quarter of the overall square has been shaded.
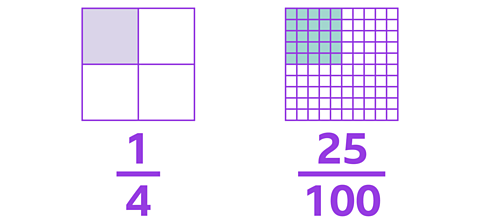
\(\frac {1} {4}\) shows that 1 part out of 4 has been shaded.
\(\frac {25} {100}\) shows that 25 parts out of 100 have been shaded.
You can see that:
\(\frac {1} {4}\) = \(\frac {25} {100}\)
So \(\frac {1} {4}\) and \(\frac {25} {100}\) are equivalent fractions.
Now let's take a look at \(\frac {25} {100}\) again, but let's rearrange the shaded parts into columns.
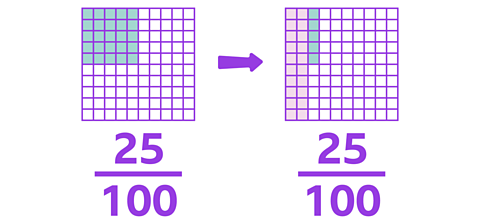
When the shaded parts are rearranged like this, you can see that you have two column of 10 and one column of 5. Or:
\(\frac {10} {100}\) + \(\frac {10} {100}\) + \(\frac {5} {100}\)
\(\frac {10} {100}\) is the same as \(\frac {1} {10}\).
You can represent this with a 0.1 decimal counter. You will need 2 of these to represent the 2 tenths.
\(\frac {5} {100}\) can be represented with 0.01 decimal counters. You will need 5 of these to represent the 5 hundredths.
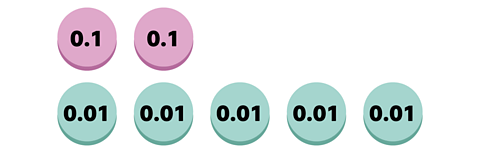
Let’s put these counters into a place value chart to help us read this as a decimal number.
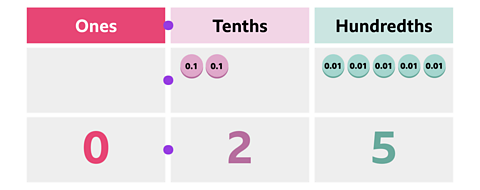
Can you see that:
\(\frac {1} {4}\) = \(\frac {25} {100}\) = 0.25
So the decimal equivalent of \(\frac {1} {4}\) is 0.25.
Three quarters as a decimal
The equivalent decimal of \(\frac {3} {4}\) is 0.75
Let's explore why…
In each of the representations below three quarters of the overall square has been shaded.
\(\frac {3} {4}\) shows that 3 parts out of 4 have been shaded.
\(\frac {75} {100}\) shows that 75 parts out of 100 have been shaded.
Finding the equivalent decimal of \(\frac {3} {4}\) is easy, when you already know the equivalent decimal of \(\frac {1} {4}\) is 0.25.
\(\frac {1} {4}\) + \(\frac {1} {4}\) + \(\frac {1} {4}\) = \(\frac {3} {4}\)
So:
0.25 + 0.25 + 0.25 = 0.75
Now, let’s use a place value chart to represent this using decimal counters.
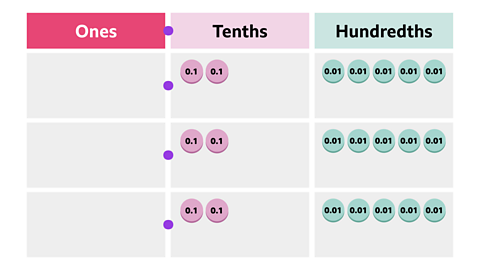
Image caption, Each row in this place value table contains the counters equivalent to one quarter. You know this is 0.25 or two tenths and five hundredths.
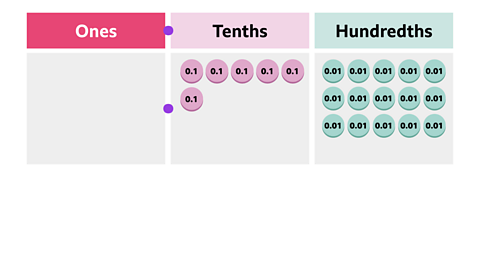
Image caption, When the counters from each row are combined into one row you can see both the total number of tenths and hundredths. In the last column, you can see that there are 15 hundredths.
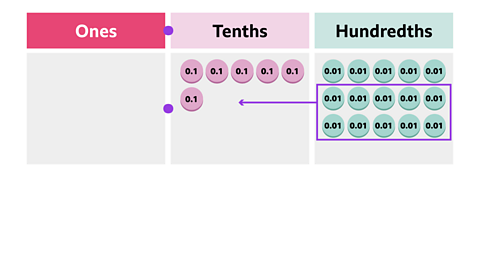
Image caption, 15 hundredths is 0.15. It is made up of 1 tenth and 5 hundredths. This 1 tenth will then be moved and added to the tenths column.

Image caption, The 10 hundredths counters have been exchanged for one tenths counter. Now that the counters are rearranged, you can see that they represent the decimal 0.75.
1 of 4
Therefore:
\(\frac {1} {4}\) + \(\frac {1} {4}\) + \(\frac {1} {4}\) = 0.25 + 0.25 + 0.25 = 0.75
So the decimal equivalent of \(\frac {3} {4}\) is 0.75.
Example
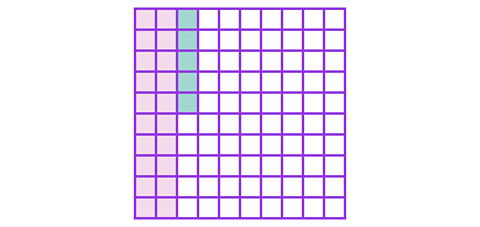
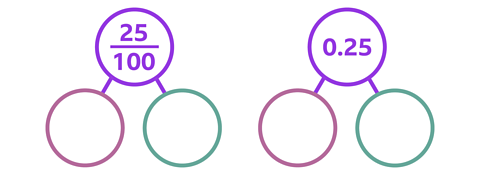
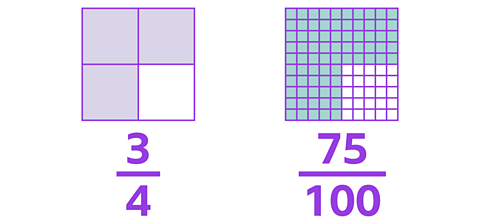
Complete the two part-whole models by partitioning \(\frac {25} {100}\) into tenths and hundredths using fractions and then decimals.
The representation of \(\frac {25} {100}\) in a hundred grid may help you.
✓ Here are the completed part-whole models.
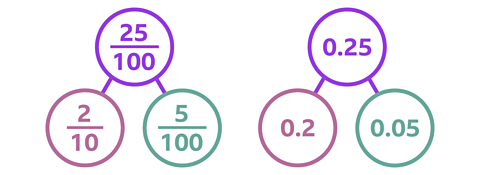
\(\frac {25} {100}\) can be partitioned as fractions into \(\frac {2} {10}\) and \(\frac {5} {100}\).
\(\frac {25} {100}\) can be partitioned as decimals into 0.2 and 0.05.
More on Fractions
Find out more by working through a topic
- count13 of 17

- count14 of 17

- count15 of 17

- count16 of 17
