Fractions in everyday life

We use fractions of amounts in everyday life - from sharing food, to working out amounts of time and even splitting into groups for activities.
Finding fractions can be used for working out discounts when shopping, for example '\( \frac{1}{3} \) off'.
Or when cooking, for example knowing how much you need to make a recipe with 'half' the ingredients.

Activity: Fractions of amounts
Complete this interactive activity to learn more about fractions of amounts and then put your knowledge to the test with a quiz.
Finding parts of a whole
To find a fraction of an amount, you start by finding out what a part is within the whole. Then you look at how many parts you need.
It can be helpful to draw a bar model to represent the calculation.
Unit fractions have a numerator of 1, for example \( \frac{1}{3} \) or \( \frac{1}{4} \).
The denominator tells you how many sections the whole number bar needs to be split into.
For example, if you wanted to find \( \frac{1}{4} \) of 12, you would split a bar of 12 in to 4 equal parts.
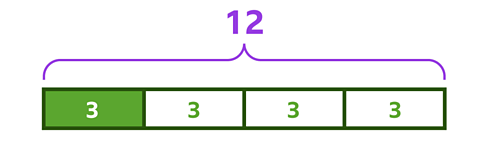
Each of those parts represents \( \frac{1}{4} \) of 12, which you can see is 3.
\( \frac{1}{4} \) of 12 = 3
Non-unit fractions have a numerator greater than 1, for example \( \frac{2}{3} \) or \( \frac{3}{4} \).
So if we wanted to find \( \frac{2}{4} \) of 12, you would draw the same bar model, but then add up 2 parts.
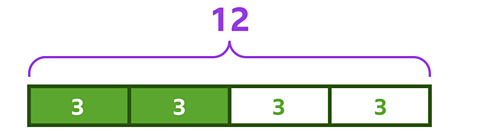
Two parts represents\( \frac{2}{4} \) of 12, which is 6.
\( \frac{2}{4} \) of 12 = 6
Example 1
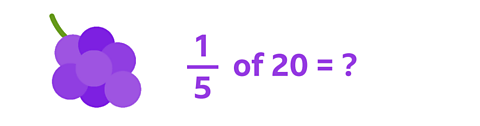
You have 20 grapes and 5 people.
Can you find out how many grapes each person gets?
✓ The bar represents the total amount in our calculation, which is 20.
You're working with fifths, so you divide the bar into 5 equal parts.
You just need one of the parts, which is 4.
\( \frac{1}{5} \) of 20 = 4

Example 2
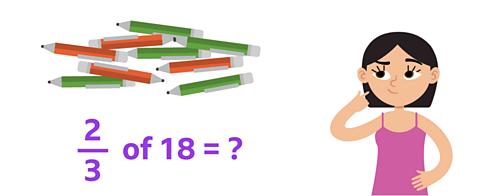
You need two thirds of these 18 pens, so everyone in the class has one.
How many are in the class?
✓ The bar needs to split 18 in to 3 equal parts.
Each of those parts is 6.
You only need \( \frac{2}{3} \) of 18, so you need 2 of the parts.
\( \frac{2}{3} \) of 18 = 12

Example 3
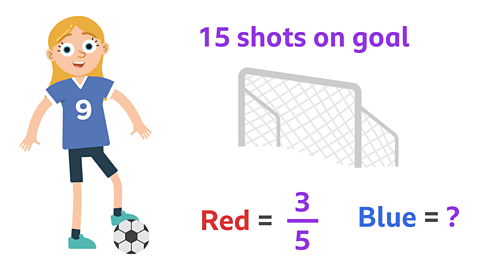
In a football match, there are fifteen shots at the goal.
The reds have three fifths of the shots and the blues have the rest.
How many shots do the blues have?
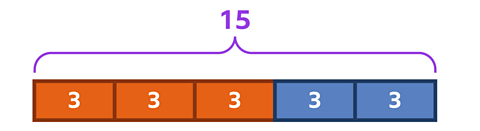
✓ The bar represents all 15 shots.
As you're working with fifths, you need to divide them into 5 equal groups. Each group represents 3 shots.
The reds have \( \frac{3}{5} \) of the shots.
The blues have the rest, which you can see is \( \frac{2}{5} \).
By adding the fifths you can see that the reds have 9 shots and the blues have 6.
\( \frac{2}{5} \) of 15 = 6
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Fractions
Find out more by working through a topic
- count14 of 17

- count15 of 17

- count16 of 17

- count17 of 17
