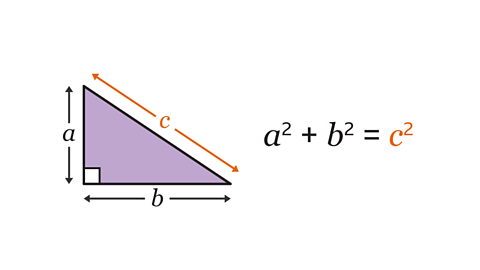Key points
trigonometryThe study of sides and angles in triangles. can be used to find a missing angle in a right-angled triangle when two sides are known.
An understanding of the three trigonometric ratios and function machines is essential.
For right-angled triangles with angle \(Ɵ\), the three trigonometric ratioA ratio written as a fraction that calculates how long one side of a right-angled triangle is compared to another, based on a given angle, Ɵ. The three main ratios are sinƟ = opposite/hypotenuse; cosƟ = adjacent/hypotenuse; and tanƟ = opposite/adjacent. are:
sin\(Ɵ\) = \(\frac{opposite}{hypotenuse}\)
cos\(Ɵ\) = \(\frac{adjacent}{hypotenuse}\)
tan\(Ɵ\) = \(\frac{opposite}{adjacent}\)
- To find a missing angle, two sides are substituteTo replace a letter with a number into one of the trigonometric equations above. The equation used must contain the two sides that are given in the question.
- To find an expressionA mathematical phrase with letters, numbers and/or operations, eg 3 × 2 + 4 for \(Ɵ\), do the inverseThe opposite of a mathematical process. E.g. the inverse of × 5 is ÷ 5. The inverse process undoes the original process. function of sin, cos or tan. The inverse functions of sin, cos and tan are sin⁻¹, cos⁻¹ and tan⁻¹.
- To work out \(Ɵ\), calculate sin⁻¹ or cos⁻¹ or tan⁻¹ of the fraction on the right-hand side. sin⁻¹ can usually be written into a scientific calculator by pressing 'shift' then 'sin', and similarly for cos⁻¹ and tan⁻¹.
- Sin, cos and tan are commonly used abbreviations for the three trigonometric functions sine, cosine and tangent.
How to calculate an unknown angle in a right-angled triangle
For a right-angled triangle, follow these steps to calculate an angle \(Ɵ\), when two sides are given:
- Choose one of the three trigonometric ratioA ratio written as a fraction that calculates how long one side of a right-angled triangle is compared to another, based on a given angle, Ɵ. The three main ratios are sinƟ = opposite/hypotenuse; cosƟ = adjacent/hypotenuse; and tanƟ = opposite/adjacent. depending on which two sides are given in the diagram:
sin\(Ɵ\) = \(\frac{opposite}{hypotenuse}\)
cos\(Ɵ\) = \(\frac{adjacent}{hypotenuse}\)
tan\(Ɵ\) = \(\frac{opposite}{adjacent}\)
- substituteTo replace a letter with a number the two sides given in the diagram into the trigonometric equation.
- To find an expression for \(Ɵ\), do theinverseThe opposite of a mathematical process. E.g. the inverse of × 5 is ÷ 5. The inverse process undoes the original process. function of sin, cos or tan. The inverse function of sin is sin⁻¹. The inverse function of cos is cos⁻¹. The inverse function of tan is tan⁻¹.
- To find the value of \(Ɵ\), calculate sin⁻¹ or cos⁻¹ or tan⁻¹ of the fraction on the right hand side. sin⁻¹ or cos⁻¹ or tan⁻¹ can usually be inputted on a scientific calculator by pressing shift before sin, cos or tan.
Note that scientific calculators need to be used for trigonometry and should be in degrees mode. Make sure there is a small D at the top of the calculator screen, and if not, go into the calculator settings to change the angle unit to 'degrees' (or 'deg').
Examples
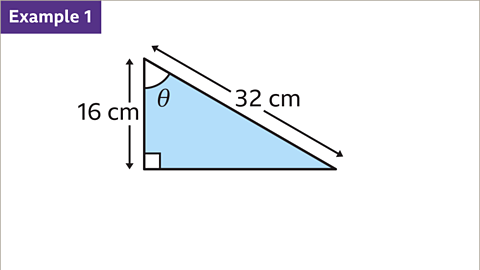
Image caption, Calculate the value of Ɵ.
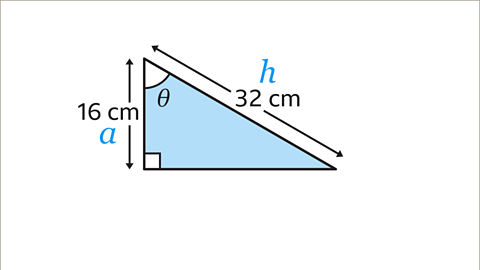
Image caption, Label the sides given. The adjacent side (𝒂) is the side between the right angle and the angle Ɵ. Label 16 cm as 𝒂. The hypotenuse (𝒉) is the longest side and is opposite the right angle. Label 32 cm as 𝒉. There is no need to label the opposite side because there is no information about its length.
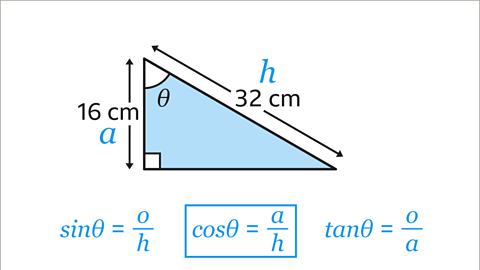
Image caption, Choose which of the three trigonometric ratios to use. The equation has to contain 𝒂 and 𝒉 because these are the sides with information in the diagram. The only equation that contains both 𝒂 and 𝒉 is the cosine (cos) ratio.
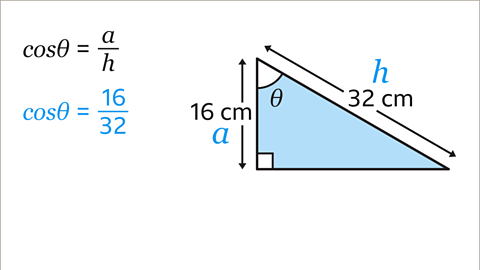
Image caption, Write down the trigonometric equation, cosƟ = 𝒂/𝒉. Substitute the values of 𝒂 and 𝒉 into the equation. 𝒂 is 16 and 𝒉 is 32. This gives cosƟ = 16/32
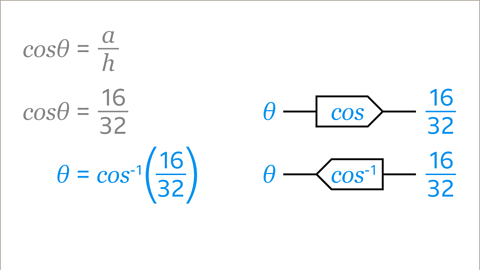
Image caption, The aim is to find the value of Ɵ that makes cosƟ equal 16/32. A function takes an input and does something to it to create an output. An inverse function takes the output and does the opposite to get back to the input. The cosine (cos) function takes the angle Ɵ and gives the answer to adjacent ÷ hypotenuse (in this example, 16/32). cos⁻¹ is the inverse function of cos. The cos⁻¹ function takes the answer to adjacent ÷ hypotenuse (in this example, 16/32), and gives the angle Ɵ. To find Ɵ, calculate cos⁻¹ (16/32).
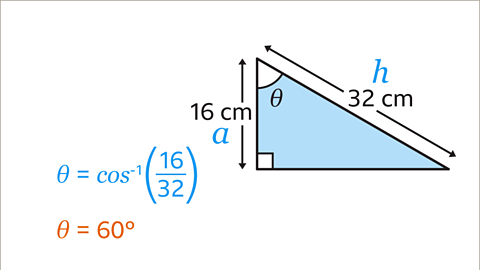
Image caption, To write cos⁻¹ on a scientific calculator, press 'shift' and 'cos'. Then type 16/32 using the fraction button. Close the brackets after typing in the fraction. The value of Ɵ is 60°.
1 of 6
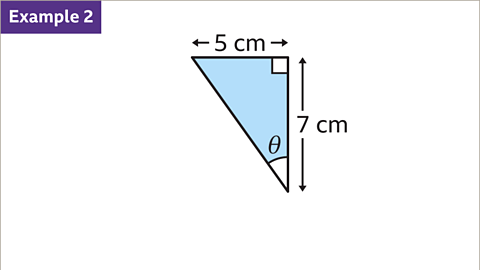
Image caption, Calculate the value of Ɵ to 1 dp.

Image caption, Label the sides given. The opposite side (𝒐) is the side opposite the angle Ɵ. Label 5 cm as 𝒐. The adjacent side (𝒂) is the side between the right angle and the angle Ɵ. Label 7 cm as 𝒂. There is no need to label the hypotenuse because there is no information about its length.
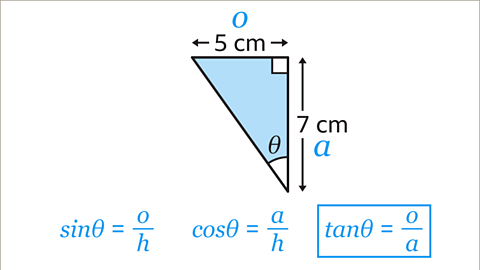
Image caption, Choose which of the three trigonometric ratios to use. The equation has to contain 𝒐 and 𝒂 because these are the sides with information in the diagram. The only equation that contains both 𝒐 and 𝒂 is the tangent (tan) ratio.
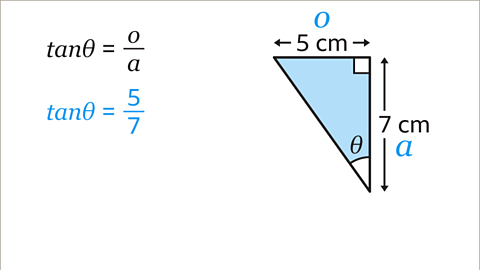
Image caption, Write down the trigonometric equation, tanƟ = 𝒐/𝒂. Substitute the values of 𝒐 and 𝒂 into the equation. 𝒐 is 5 and 𝒂 is 7. This gives tanƟ = 5/7
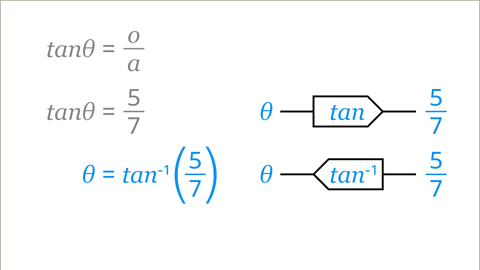
Image caption, The aim is to find the value of Ɵ that makes tanƟ equal 5/7. A function takes an input and does something to it to create an output. An inverse function takes the output and does the opposite to get back to the input. The tan function takes the angle Ɵ and gives the answer to opposite ÷ adjacent (in this example, 5/7). tan⁻¹ is the inverse function of tan. The tan⁻¹ function takes the answer to opposite ÷ adjacent (in this example, 5/7) and gives the angle Ɵ. To find Ɵ, calculate tan⁻¹ (5/7).
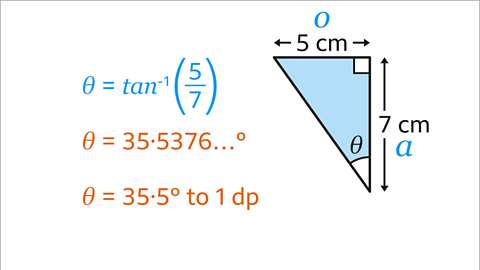
Image caption, To write tan⁻¹ on a scientific calculator, press 'shift' and 'tan'. Then type 5/7 using the fraction button. Close the brackets after typing in the fraction. The value of Ɵ is 35.5376….°. Round the answer to one decimal place to give Ɵ = 35.5°.
1 of 6
Question
Which trigonometric ratio would be used to find \(Ɵ\)?
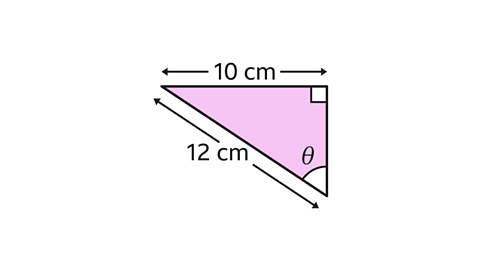
The correct trigonometric ratio is sin\(Ɵ\) = \(\frac{o}{h}\).
Label the sides given. 12 cm should be labelled as hypotenuse (\(h\)) because it is the longest side and is opposite the right angle.
10 cm should be labelled as opposite (\(o\)) because it is opposite the angle \(Ɵ\).
There is no need to label the adjacent side because there is no information about its length.
The trigonometric ratio chosen has to contain \(o\) and \(h\) because these are the sides with information in the diagram.
The only equation that contains both \(o\) and \(h\) is the sine (sin) ratio.
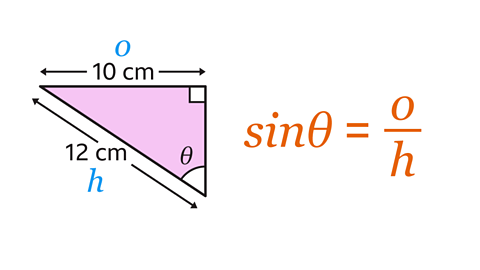
Practise finding angles in right-angled triangles
Practise finding angles in right-angled triangles with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

Architecture is the design and construction of buildings.
Architects use trigonometry in their designs to ensure structures are safe from weather, external forces and weight from other parts of the building.
Without checking angles of the construction with trigonometry, buildings would be unstable and bridges would collapse.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Pythagoras and trigonometry
Find out more by working through a topic
- count1 of 5
- count2 of 5