Key points
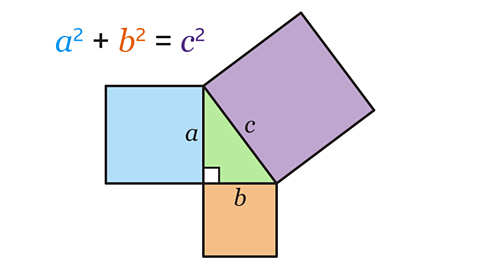
- Pythagoras’ theorem states that for any right-angled triangle, the area of the square on the hypotenuseThe longest side of a right-angled triangle, which is always opposite the right angle. When labelling a length as the hypotenuse, it can be shortened to 𝒉. is equal to the sum of the areas of the squares on the other two sides.
- It can be thought of as \(a\)² + \(b\)² = \(c\)² where \(a\) and \(b\) are the shorter sides of the triangle, and \(c\) is the hypotenuse (longest side).
- Pythagoras’ theorem is only true for right-angled triangles. It is possible to check if a triangle is right-angled bysubstituteIn algebra substitute means to replace a letter (or variable) with a number. in the lengths of the sides and seeing if the value of \(a\)² + \(b\)² is the same as the value of \(c\)².
- Pythagoras’ theorem can be used to find a missing side of a right-angled triangle. To find the hypotenuse, substituteIn algebra substitute means to replace a letter (or variable) with a number. the values of \(a\)² and \(b\)² into the equation, and solve to find \(c\). This will involve adding the two squares and finding the square root √A value that, when multiplied by itself, gives the number. Eg, 4 × 4 = 16, so the square root of 16 is 4. √16 = 4 of the answer.
- To find a shorter side, substitute the values into the equation and solve to find \(a\) or \(b\). This will involve subtracting the two squares and finding the square root of the answer.
- An understanding of powers and roots is essential before exploring this topic.

What is Pythagoras' theorem?
Pythagoras’ theorem is a statement that is true for all right-angled triangles.It states that the area of the square on the hypotenuseThe longest side of a right-angled triangle, which is always opposite the right angle. When labelling a length as the hypotenuse, it can be shortened to 𝒉. is equal to the sum of the area of the squares on the other two sides.
It is useful to think of Pythagoras’ theorem as \(a\)² + \(b\)² = \(c\)².
The hypotenuse is labelled as \(c\) and the other two sides labelled as \(a\) and \(b\). This makes the areas of the squares \(c\)², \(a\)² and \(b\)².
Examples
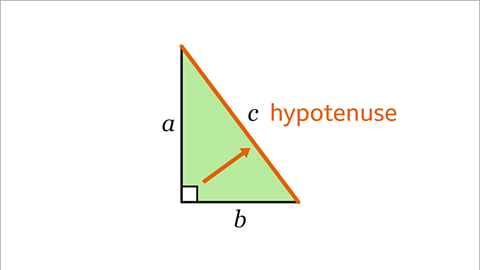
Image caption, The hypotenuse is the longest side of a right-angled triangle. It is always opposite the right angle. To label a right-angled triangle to use Pythagoras’ theorem, the hypotenuse should be labelled as 𝒄. The other two sides should be labelled 𝒂 and 𝒃. It does not matter which way round 𝒂 and 𝒃 are labelled.
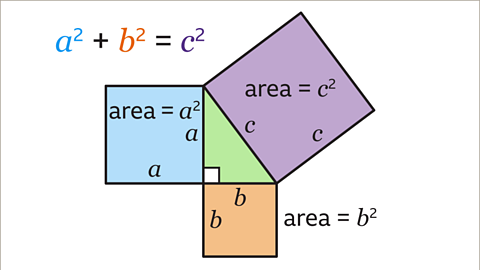
Image caption, The area of the blue square is 𝒂 x 𝒂, which is 𝒂². The area of the orange square is 𝒃 x 𝒃, which is 𝒃². The area of the purple square on the hypotenuse is 𝒄 x 𝒄, which is 𝒄². Pythagoras’ theorem states that for any right-angled triangle, the area of the square on the hypotenuse is equal to the sum of the area of the squares on the other two sides. Here the area of the blue square plus the area of the orange square equals the area of the purple square. In other words, 𝒂² + 𝒃² = 𝒄²
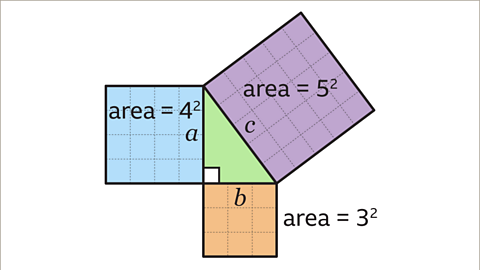
Image caption, For this triangle, 𝒂 = 4, 𝒃 = 3, and 𝒄 = 5. The area of the blue square is 4 x 4, or 4². The area of the orange square is 3 x 3, or 3². The area of the purple square is 5 x 5, or 5²
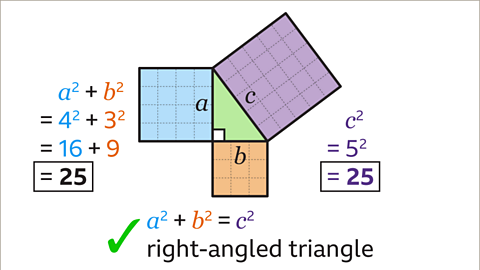
Image caption, Pythagoras’ theorem works for this triangle because the value of 𝒂² + 𝒃² is 25, and the value of 𝒄² is also 25. In other words, the area of the blue and the orange square added together is the same as the area of the purple square. Pythagoras’ theorem is only true for right-angled triangles. As 𝒂² + 𝒃² = 𝒄², the triangle must be a right-angled triangle.
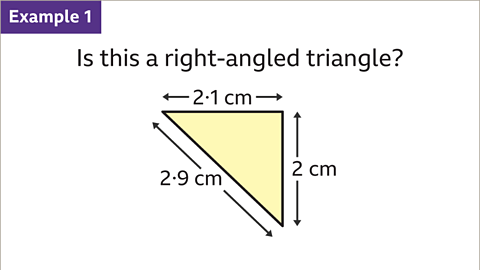
Image caption, This triangle looks like a right-angled triangle, but it might not be. To find out if it is a right-angled triangle check if Pythagoras’ theorem is true for the lengths of the sides.
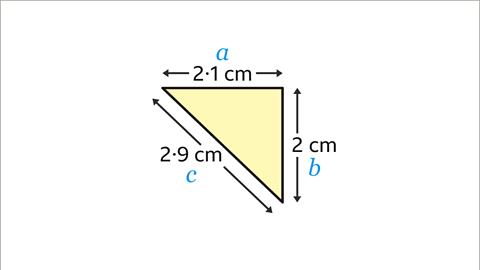
Image caption, To check if Pythagoras’ theorem is true for this triangle, the sides should be labelled 𝒂, 𝒃 and 𝒄. The longest side is always labelled 𝒄. It doesn’t matter which way round 𝒂 and 𝒃 are labelled. Here, 𝒂 is 2.1 cm, 𝒃 is 2 cm and 𝒄 is 2.9 cm.
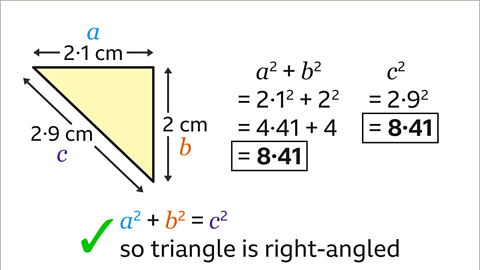
Image caption, From substituting in the lengths, the value of 𝒂² + 𝒃² is 2.1² + 2² = 8.41, and the value of 𝒄² is 2.9² which is also 8.41. 𝒂² + 𝒃² is the same as 𝒄². Pythagoras’ theorem is only true for right-angled triangles. As 𝒂² + 𝒃² = 𝒄², the triangle must be a right-angled triangle.
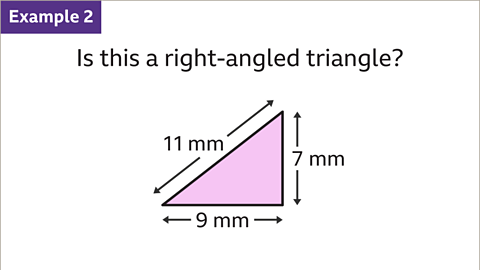
Image caption, This triangle looks like a right-angled triangle, but it might not be. To find out if it is a right-angled triangle, check if Pythagoras’ theorem is true for the lengths of the sides.
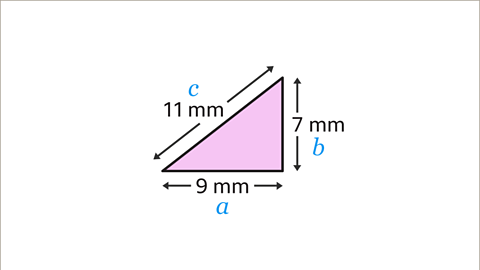
Image caption, Firstly, the sides 𝒂, 𝒃 and 𝒄 should be labelled. The longest side is always labelled 𝒄. It doesn’t matter which way round 𝒂 and 𝒃 are labelled. Here, 𝒂 is 9 mm, 𝒃 is 7 mm and 𝒄 is 11 mm.
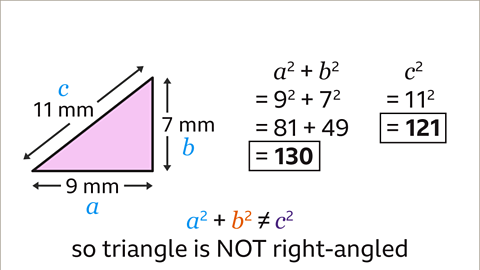
Image caption, Substitute in the lengths. The value of 𝒂² + 𝒃² is 9² + 7² = 130, and the value of 𝒄² is 11² which is 121. Pythagoras’ theorem is always true for right-angled triangles. 130 is not the same as 121. As 𝒂² + 𝒃² does not equal 𝒄², the triangle cannot be a right-angled triangle. (Please note that “≠” is the "not-equals" sign and the opposite of "=")
1 of 10
Question
Show that the triangle is a right-angled triangle using Pythagoras’ theorem.
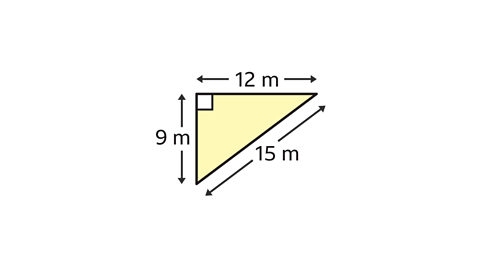
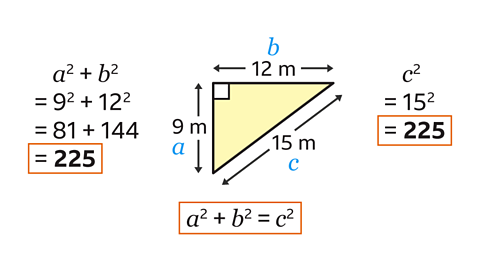
For a triangle to be right-angled, it must satisfy Pythagoras’ theorem:
\(a\)² + \(b\)² = \(c\)².
Label the sides \(a\), \(b\) and \(c\). \(c\) is the hypotenuse, which is the longest side. It does not matter which way round \(a\) and \(b\) are labelled.
\(a\)² + \(b\)² = 9² + 12² = 81 + 144 = 225
For the triangle to be right-angled, the value of \(c\)² must also be 225. The value of \(c\)² is 15² = 225
The value of \(a\)² + \(b\)² Is the same as the value of \(c\)². Therefore, the triangle is right-angled.
Finding the length of the hypotenuse
Pythagoras’ theoremPythagoras’ theorem states the relationship between sides in a right-angled triangle. It states that 𝒂² + 𝒃² = 𝒄², where 𝒄 is the hypotenuse (longest side), and 𝒂 and 𝒃 are the other two sides. can be used to calculate a missing side in a right-angled triangle. Follow these steps to find the length of the hypotenuseThe longest side of a right-angled triangle, which is always opposite the right angle. When labelling a length as the hypotenuse, it can be shortened to 𝒉. when the other two sides are given.
Label the sides \(a\), \(b\) and \(c\). Remember, the hypotenuse should always be labelled \(c\).
Then substituteIn algebra substitute means to replace a letter (or variable) with a number. the values of \(a\) and \(b\) into the equation \(a\)² + \(b\)² = \(c\)².
Add the squares together to get the value of \(c\)².
Square root the value of \(c\)² to get the value of \(c\).
Examples

Image caption, Find the length of LN
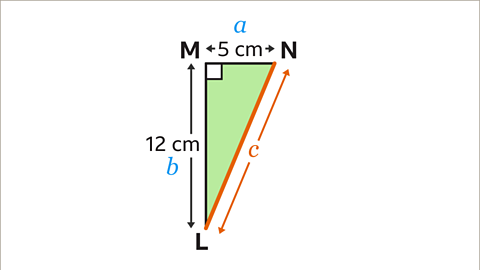
Image caption, LN is the length from L to N. Label the sides 𝒂, 𝒃 and 𝒄. The hypotenuse is the longest side opposite the right angle, and should be labelled 𝒄. It does not matter which way round 𝒂 and 𝒃 are labelled.
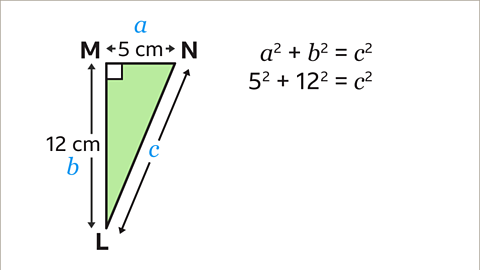
Image caption, Substitute the values into the equation 𝒂² + 𝒃² = 𝒄². 𝒂² = 5² and 𝒃² = 12². 𝒄² is not known and is the length LN that is needed, so keep this as 𝒄².
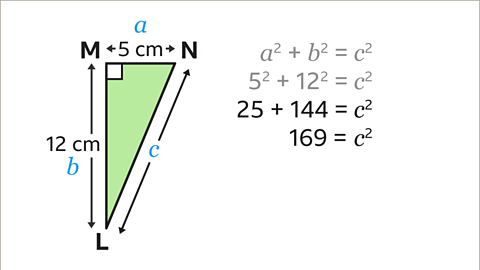
Image caption, Calculate the value of the squares. 5² = 25, and 12² = 144. Add the squares together to get 169. This is the value of 𝒄².
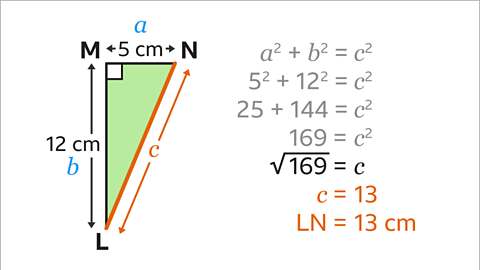
Image caption, The inverse of squaring is square rooting, so to find 𝒄, calculate the square root of 169. This gives the answer of 𝒄 = 13. Therefore LN = 13 cm.
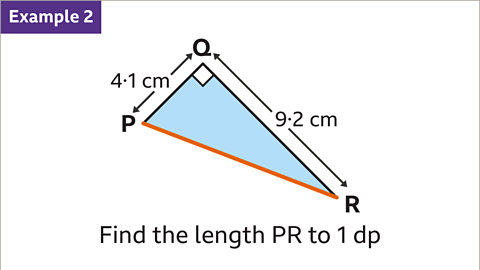
Image caption, Find the length PR to 1 decimal place.
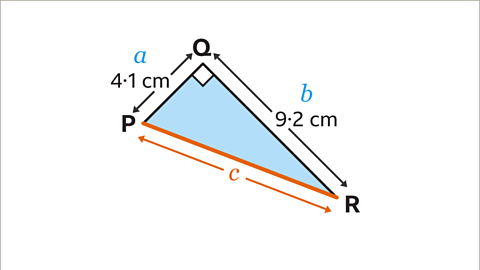
Image caption, PR is the length from P to R. Label the sides 𝒂, 𝒃 and 𝒄. The hypotenuse should be labelled 𝒄. It does not matter which way round 𝒂 and 𝒃 are labelled.
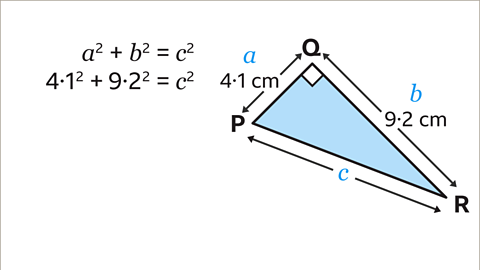
Image caption, Substitute the values into the equation 𝒂² + 𝒃² = 𝒄². 𝒂² = 4.1² and 𝒃² = 9.2². 𝒄² is not known and is the length PR that is needed, so keep this as 𝒄².
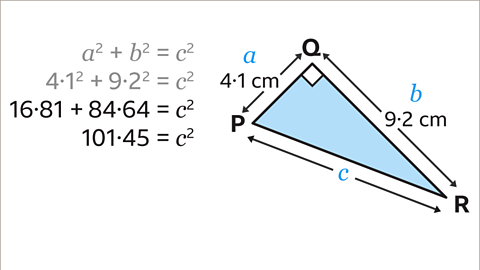
Image caption, Calculate the value of the squares with a calculator. 4.1² = 16.81 and 9.2² = 84.64. Add the squares together to get 101.45. This is the value of 𝒄².
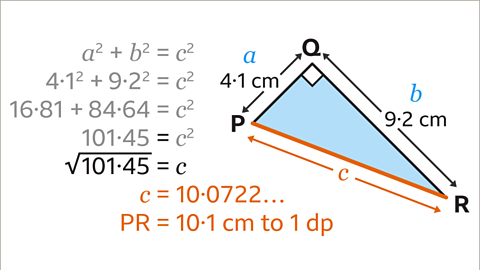
Image caption, The inverse (opposite) of squaring is square rooting, so to find 𝒄, calculate the square root of 101.45. This gives the answer of 𝒄 = 10.0722... Therefore, when rounded to 1 decimal place, PR = 10.1 cm.
1 of 10
Question
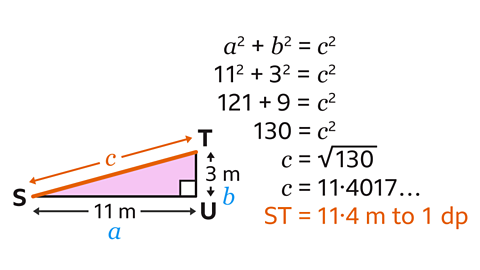
Find the length ST to 1 decimal place.
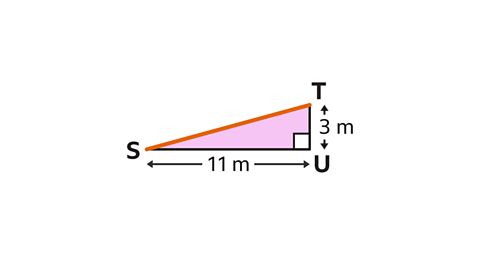
ST is the length from S to T. ST is the hypotenuse, so should be labelled as \(c\). 11 m can be labelled as \(a\) and 3 m can be labelled as \(b\).
Substitute these values into \(a\)² + \(b\)² = \(c\)² to give 11² + 3² = \(c\)².
11² is 121. 3² is 9
Add the two squares together to give \(c\)² = 130
To find \(c\), the inverse of squaring is square rooting, so \(c\)=√130 = 11.4017…
When rounded to 1 decimal place, this gives ST = 11.4 m.
Finding the length of another side
Follow these steps to find the length of a side that is not the hypotenuse.
Label the sides \(a\), \(b\), and \(c\). Remember the hypotenuseThe longest side of a right-angled triangle, which is always opposite the right angle. When labelling a length as the hypotenuse, it can be shortened to 𝒉. should always be labelled \(c\)
Then substituteIn algebra substitute means to replace a letter (or variable) with a number. the values of \(a\) and \(b\) into the equation \(a\)² + \(b\)² = \(c\)²
If finding \(b\), subtract the squares to get the value of \(b\)²
Finally, square rootA number whose square is equal to the given number, √9 = 3, 3² = 9. The value may also be negative, eg (-3)² = 9 the value of \(b\)² to get the value of \(b\)
Examples
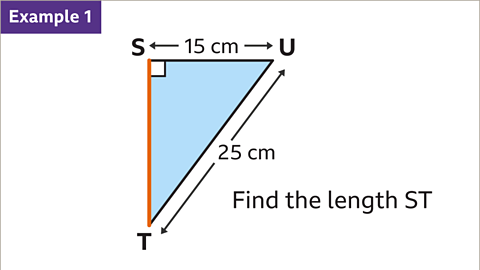
Image caption, Find the length ST
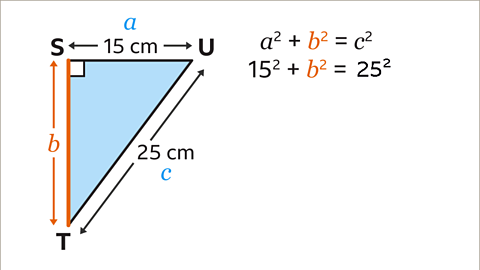
Image caption, ST is the length from S to T. Label the sides 𝒂, 𝒃 and 𝒄. The hypotenuse should be labelled 𝒄. It does not matter which way round 𝒂 and 𝒃 are labelled as the result will be the same. Substitute the values into the equation 𝒂² + 𝒃² = 𝒄². 𝒂² = 15² and 𝒄² = 25². 𝒃² is not known and is the length ST that is needed, so keep this as 𝒃². This leads to the equation 15² + 𝒃² = 25².
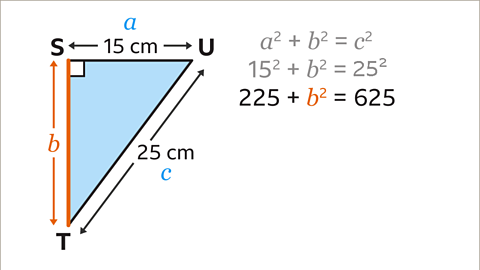
Image caption, Calculate the value of the squares with a calculator. 15² = 225 and 25² = 625. This leads to the equation 225 + 𝒃² = 625
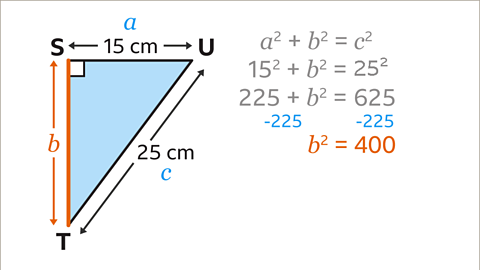
Image caption, To work out the value of 𝒃², subtract 225 from both sides of the equation. This leads to the equation 𝒃² = 400
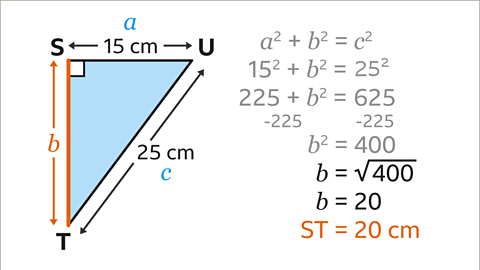
Image caption, The inverse of squaring is square rooting, so to find 𝒃, calculate the square root of 400. This gives the answer of 𝒃 = 20. Therefore ST = 20 cm.
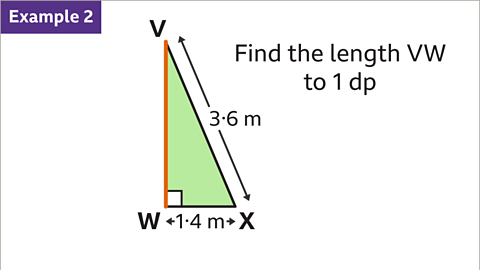
Image caption, Find the length VW to 1 decimal place (d p).
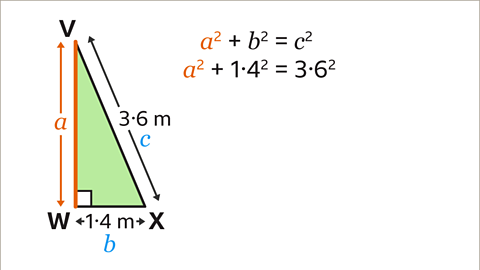
Image caption, VW is the length from V to W. Label the sides 𝒂, 𝒃 and 𝒄. The hypotenuse should be labelled 𝒄. It does not matter which way round 𝒂 and 𝒃 are labelled as the result will be the same. Substitute the values into the equation 𝒂² + 𝒃² = 𝒄². 𝒃² = 1.4² and 𝒄² = 3.6². 𝒂² is not known and is the length VW that is needed, so keep this as 𝒂². This leads to the equation 𝒂² + 1.4² = 3.6²
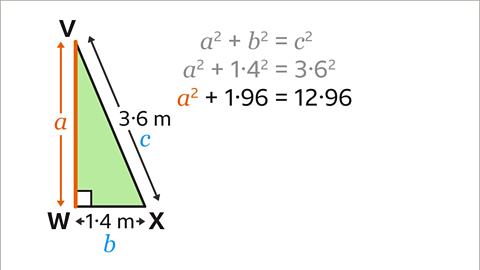
Image caption, Calculate the value of the squares using a calculator. 1.4² = 1.96 , and 3.6² = 12.96. This leads to the equation 𝒂² + 1.96 = 12.96
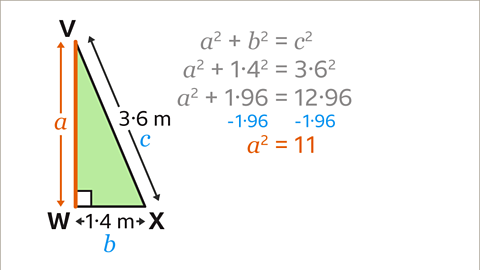
Image caption, To work out the value of 𝒂², subtract 1.96 from both sides of the equation. This leads to the equation 𝒂² = 11
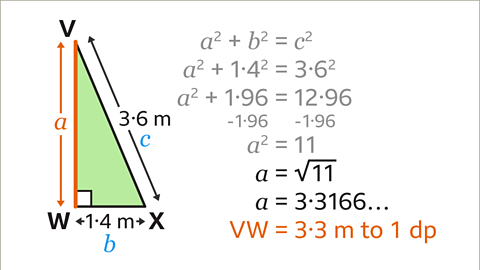
Image caption, The inverse of squaring is square rooting, so to find 𝒂, calculate the square root of 11. This gives the answer of 𝒂 = 3.3166… Therefore to 1 decimal place, VW = 3.3 m.
1 of 10
Question
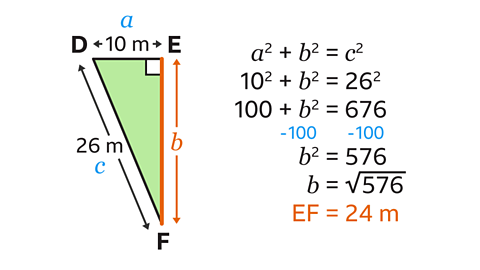
Find the length EF.
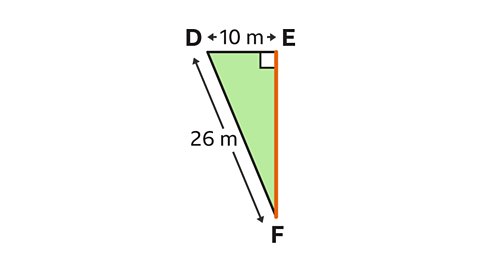
EF is the length from E to F.
26 m is the hypotenuse, so should be labelled as \(c\). 10 m can be labelled as \(a\) and EF can be labelled as \(b\).
Substitute these values into \(a\)² + \(b\)² = \(c\)² to give 10² + \(b\)² = 262
10² is 100. 26² is 676. This leads to the equation 100 + \(b\)² = 676
Subtract 100 from both sides to give \(b\)² = 576
To find \(b\), the inverse of squaring is square rooting, so \(b\)=√576=24
Therefore, EF = 24 m.
Practise using Pythagoras' theorem
Quiz
Practise calculating different lengths of sides using Pythagoras' theorem with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths

Flat screen televisions are usually measured diagonally from opposite corners of the screen.
This means that a 55 inch television does not have a width of 55 inches.It would measure 55 inches from the top left corner to the bottom right corner (as opposite.)
Pythagoras’ theorem can be used to calculate the diagonal size of the television screen, if the width and the height are known.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Pythagoras and trigonometry
Find out more by working through a topic
- count2 of 5
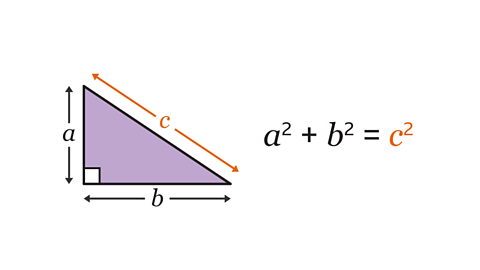
- count5 of 5