Key points
The Complement (of a set) (symbol 𝑨’)On a Venn diagram, the region that is not in the set. 𝑷’ is the complement of set 𝑷 and is the region outside the circle for set 𝑷. 𝑷’ = {elements that are not in 𝑷}. of a setA collection of information or letters or numbers. The members of the set can be listed inside curly brackets,{ }. A set may be described in words inside curly brackets { }. On a Venn diagram a set is shown as a circle. contains all the elementA piece of information, a letter or a number, in a set. Also described as a member of the set. that are not in the set. A set plus the complement of a set is the the universal set (symbol ξ)The set of all the elements being considered. The Greek letter ξ (Xi) is used..
On a Venn diagramA simple visual diagram with overlapping circles, used to show the relationships between two different groups or sets. the complement of a set is the regionAn identified area on a diagram or graph. outside the circle that represents the set.
\(P’\) is the complement of set \(P\).
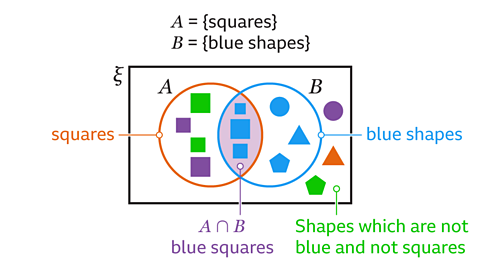
The intersection of one set and the complement of another set identifies elements with the attributes of one set and none of the attributes of the other set. This can be used to classify shapes and to support probability calculations.

Understanding the complement of a set
To list the elements of the complement of set \(P\):
- \(P'\) contains all the elements that are not in set \(P\). These are the elements in the universal set that are not in set \(P\).
To identify the complement of a set \(P\) on a Venn diagram:
- \(P'\) is the region outside the circle that represents set \(P\).
Examples

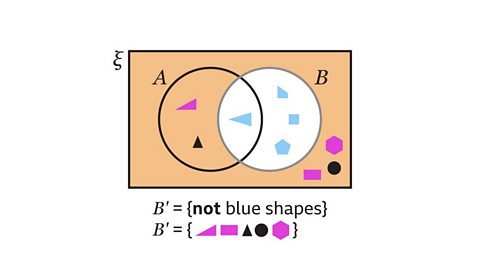
Image caption, Describe 𝑩’, the complement of set 𝑩, and list the elements in 𝑩’.
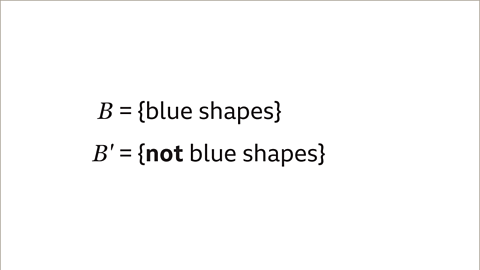
Image caption, 𝑩 = {blue shapes}. The complement of set 𝑩 is 𝑩’. 𝑩’ is the set of shapes that are not blue.

Image caption, The elements of 𝑩’ can be listed. These are all the shapes that are in the universal set (ξ) that are not in set 𝑩.

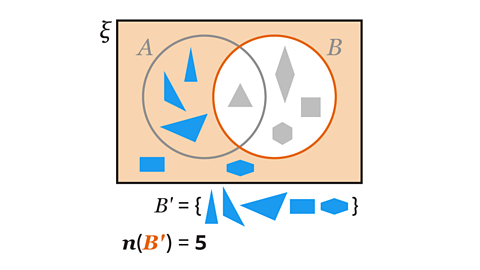
Image caption, The Venn diagram shows shapes sorted into the sets 𝑨 and 𝑩. 𝑨 = {triangles} and 𝑩 = {blue shapes}. Show the region for the complement of set 𝑩, 𝑩’.
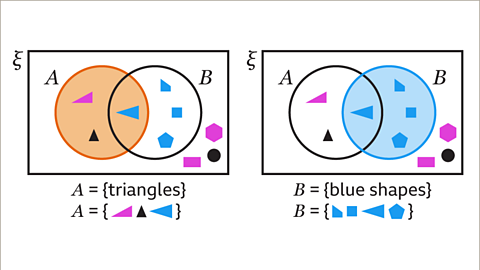
Image caption, Set 𝑨 contains all the triangles. The elements of set 𝑨 are one purple, one black and one blue triangle. Set 𝑩 contains all blue shapes. The elements of set 𝑩 are a blue trapezium, a blue square, a blue triangle and a blue pentagon.
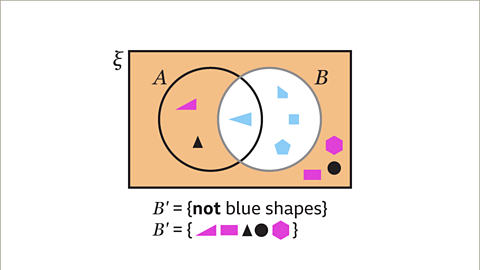
Image caption, The complement of set 𝑩, 𝑩’, contains all the elements that are not in set 𝑩. These shapes are in the region outside the circle that represents set 𝑩. The elements in 𝑩’ are a purple triangle, a purple rectangle, a black triangle, a black circle and a purple hexagon. The region is outside the circle that represents set 𝑩.

Image caption, ξ = {factors of 100}. 𝑨 = {factors of 20}. 𝑩 = {multiples of 10}. Identify and describe the region of 𝑨’, the complement of set 𝑨, on a Venn diagram.
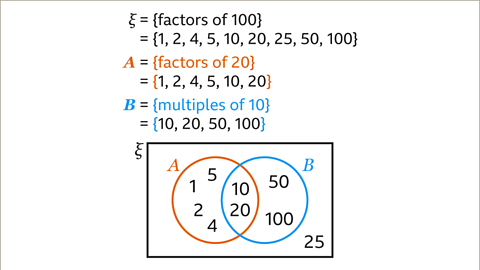
Image caption, List the elements of each set ξ = {1, 2, 4, 5, 10, 20, 25, 50, 100}. 𝑨 = {1, 2, 4, 5, 10, 20} and 𝑩 = {10, 20, 50, 100}. The Venn diagram shows the sets. The complement of set 𝑨, 𝑨’, contains all the elements that are not in set 𝑨.
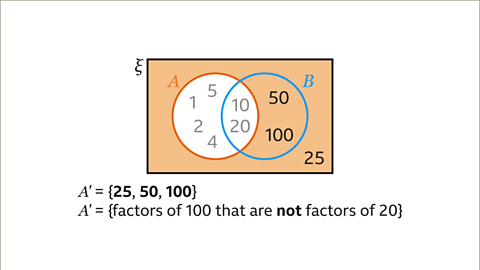
Image caption, 𝑨’ is the complement of set 𝑨, containing all the elements not in set 𝑨. These elements are outside the circle of set 𝑨. 𝑨’ may be described as ‘the factors of 100 that are not factors of 20’.
1 of 9
Question
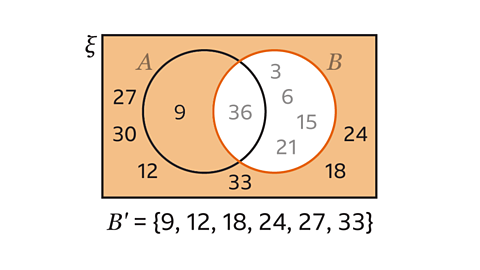
The Venn diagram shows \(ξ\) = {multiples of 3 less than 40}, \(A\) = {square numbers}, \(B\) = {triangular numbers}.
List the elements of \(B’\).
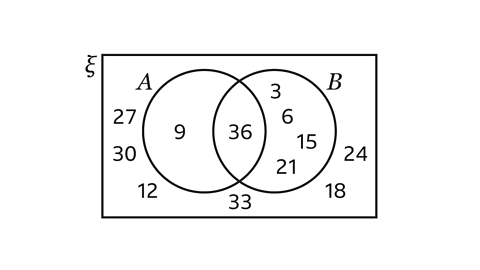
\(ξ\) = {multiples of 3 less than 40}
\(ξ\) = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36}
\(A\) = {square numbers}
\(A\) = {9, 36}
\(B\) = {triangular numbers}
\(B\) = {3, 6, 15, 21, 36}
\(B’\) is the complement of set \(B\), \(B’\) contains the elements that are not in set \(B\). These are the elements in the region outside the circle for set \(B\).
\(B’\) = {9, 12, 18, 24, 27, 30, 33}
Practise working out the complement of a set
Practise working out the complement of a set with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Sets and Venn diagrams
Find out more by working through a topic
- count5 of 5
- count1 of 5
- count2 of 5
- count3 of 5