Key points
- Venn diagramA diagram used to sort data. are a visual way of representing setA collection of information or letters or numbers. The members of the set can be listed inside curly brackets, { }. A set may be described in words inside curly brackets { }. On a Venn diagram a set is shown as a circle.. They consist of one or more circles inside a rectangle. The circles usually overlap.
- All the data being considered is contained inside the rectangle. This is called the universal set (ξ)The set of all the elements being considered. The Greek letter ξ (Xi) is used to represent the universal set. and is represented by the Greek letter ξ (Xi). Each circle represents a set.
- Set notationAn agreed form of presentation for mathematical information. is used to describe different regions of a Venn diagram.

Understanding and interpreting a Venn diagram
Set notation is used to describe different regionAn identified area on a diagram or graph. on a Venn diagram:
- ξ represents the universal set.
- A represents set A and B represents set B, usually a capital letter is used.
- A∩B represents the intersection (of sets) (∩)On a Venn diagram, the region where sets overlap. 𝑷∩𝑸 is the intersection of set 𝑷 and set 𝑸. 𝑷∩𝑸 = {elements in 𝑷 that are also in 𝑸}. of set A and set B.
- A∪B represents the union (of sets) (∪)On a Venn diagram, the region of two or more sets when they are combined. 𝑷∪𝑸 is the union of set 𝑷 and set 𝑸. 𝑷∪𝑸 = {elements just in 𝑷, in both 𝑷 and 𝑸, just in 𝑸}. of set A and set B.
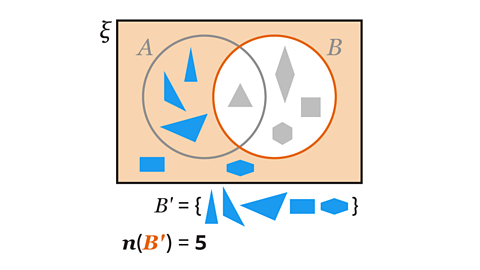
- A’ represents the complement (of a set)On a Venn diagram, the region that is not in the set. P’ is the complement of set P and is the region outside the circle for set P. P’ = {elements that are not in P}. of set A.
The elements for each region of a Venn diagram can be written with the set notation equal to the list of element (maths)A piece of information or a letter, or a number, in a set. Also described as a member of the set. inside curly brackets { }.
When sets intersect (overlap), the elements in the intersection are members of both sets. When the sets have no elements in common, the overlap is empty or the circles do not overlap.
Examples
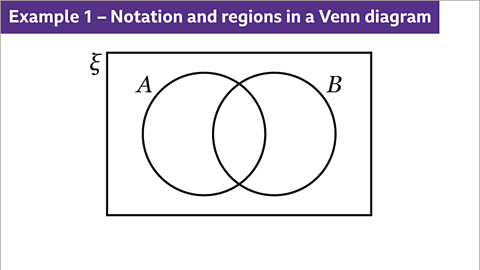
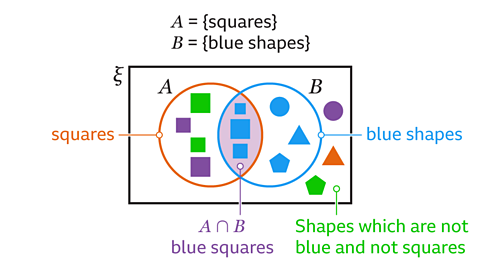
Image caption, Describe each region of the Venn diagram using set notation.
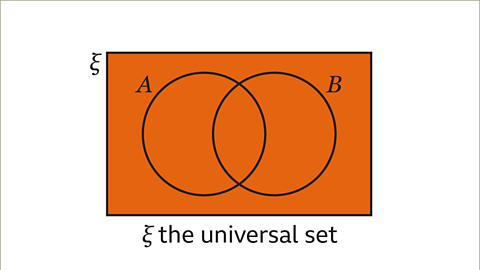
Image caption, The whole rectangle contains all the elements being considered. This is called the universal set, represented by the Greek letter ξ (Xi).
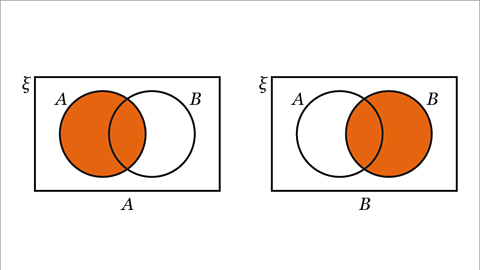
Image caption, A is the region representing set A, this is contained inside the circle labelled A. B is the region representing set B, this is contained inside the circle labelled B.
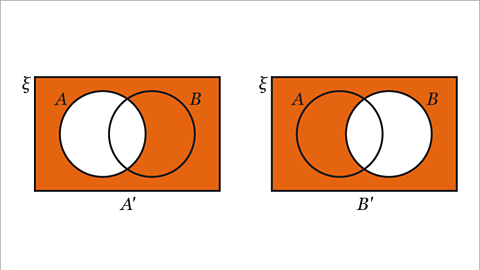
Image caption, A’ is the complement of A. This is the region that is not set A. It is the region outside the circle for set A. B’ is the complement of B. This is the region that is not set B. It is the region outside the circle for set B.
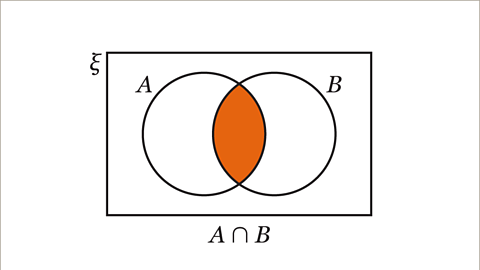
Image caption, The overlap between sets is called the intersection. The notation for the intersection of set A and set B is A∩B. The intersection contains elements that are in both set A and set B.
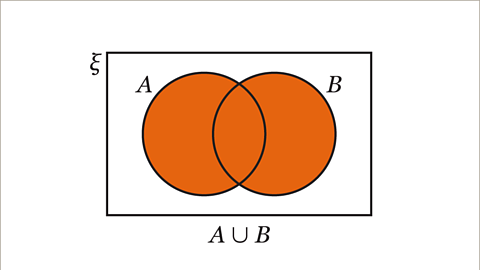
Image caption, The combination of sets is the union. The notation for the union of set A and set B is A∪B. The union of set A and set B contains the elements that are in set A, the elements that are in set B and the elements that are in both set A and set B.
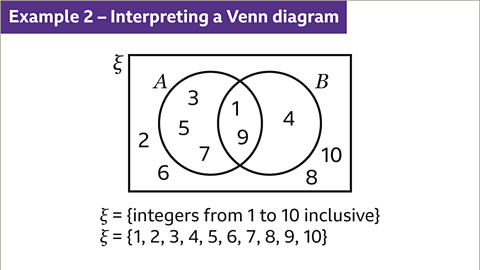
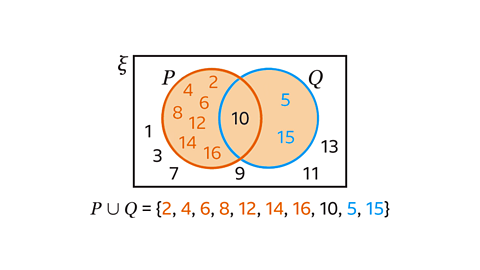
Image caption, Describe and list the elements in set A, set B and the intersection of set A and set B. The universal set is the set of integers from 1 to 10 inclusive, ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
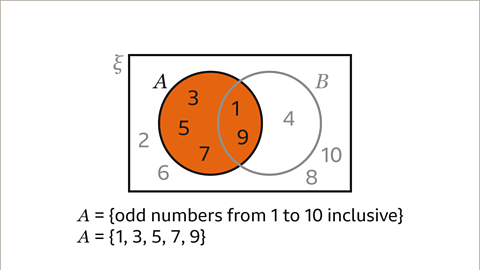
Image caption, Set A can be described as the set of odd numbers from 1 to 10 inclusive. In set notation this is A = {odd numbers from 1 to 10 inclusive}. The elements in set A are 1, 3, 5, 7 and 9. In set notation this is A = {1, 3, 5, 7, 9}.
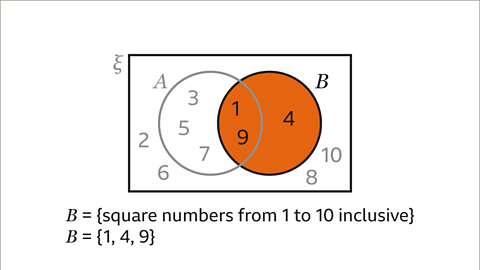
Image caption, Set B can be described as the set of square numbers from 1 to 10 inclusive. In set notation this is B = {square numbers from 1 to 10 inclusive}. The elements in set B are 1, 4, and 9. In set notation this is B = {1, 4, 9}.
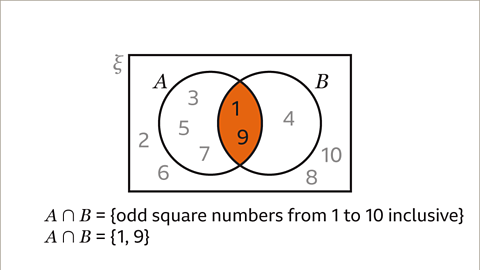
Image caption, The intersection of set A and set B, A∩B, contains the numbers from 1 to 10 inclusive that are odd and square. A∩B = {1,9}. The only odd square numbers from 1 to 10 inclusive are 1 and 9
1 of 10
Question
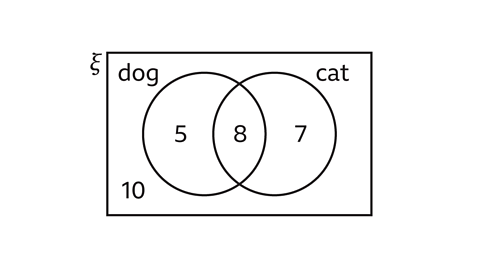
30 people answered a survey about whether they have a dog or a cat. The Venn diagram shows the information from the survey.
Answer the following questions:
- How many people have got a dog?
- How many people have only got a cat?
- How many people have a cat and a dog?
- How many people do not own a cat?
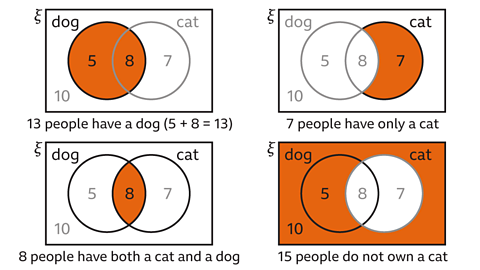
13 people have got a dog. The circle for the set of people with a dog has 5 people who just have a dog and 8 people who have both a cat and a dog, this gives a total of 13 people with a dog.
7 people have only got a cat. This is the number of people in the set of people with a cat who do not have a dog.
8 people have a cat and a dog. This is the number of people in the intersection of the set of people with a dog and the set of people with a cat.
15 people do not own a cat. This is the total of the people that are not in the set of people who own a cat (the complement of cat owners).
Drawing Venn diagrams
- To draw Venn diagramA diagram used to sort data. with two overlapping setA collection of information or letters or numbers. The members of the set can be listed inside curly brackets, { }. A set may be described in words inside curly brackets { }. On a Venn diagram a set is shown as a circle. A and B:
- Write each set as a list of element (maths)A piece of information or a letter, or a number, in a set. Also described as a member of the set..
- Write the elements that are in both sets in the intersection (of sets) (∩)On a Venn diagram, the region where sets overlap. 𝑷∩𝑸 is the intersection of set 𝑷 and set 𝑸. 𝑷∩𝑸 = {elements in 𝑷 that are also in 𝑸}., A∩B.
- Write the rest of the elements that are just in set A.
- Write the rest of the elements that are just in set B.
- Write any remaining elements from the universal set (ξ)The set of all the elements being considered. The Greek letter ξ (Xi) is used to represent the universal set. in the space inside the rectangle and outside the circles.
- To avoid errors:
- Make sure that the number of elements in the Venn diagram is equal to the number of elements in the universal set.
- Check that a set does not include an element that is not in the universal set.
Examples

Image caption, Draw a Venn diagram for ξ = {positive whole numbers less than 10}, A = {prime numbers} and B = {even numbers}. Write each set as a list of elements. ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 3, 5, 7} and B = {2, 4, 6, 8}.
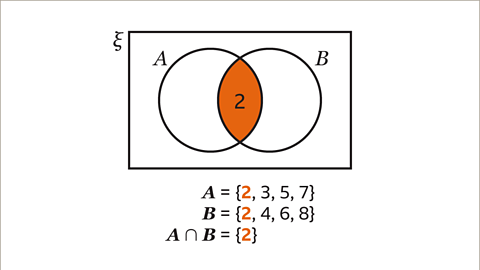
Image caption, Draw a rectangle for the universal set and two overlapping circles, one for set A and one for set B. Write the elements that are in both sets in the intersection, A∩B. One number is prime and even. A∩B = 2
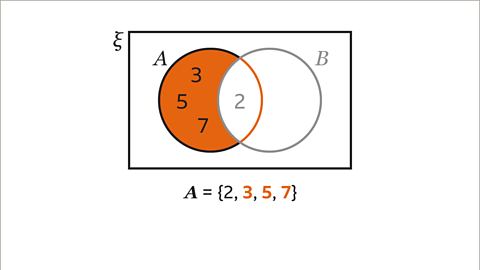
Image caption, Write the rest of the elements that are just in set A. The number 2 has already been entered, 3 5 and 7 are the rest of the prime numbers that are in set A.
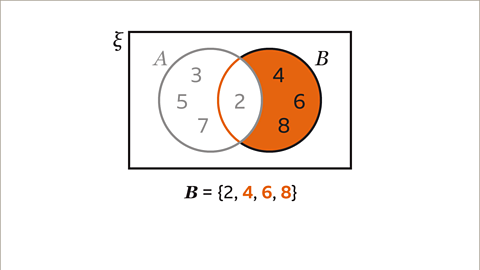
Image caption, Write the rest of the elements that are just in set B. The number 2 has already been entered, 4, 6 and 8 are the rest of the even numbers in set B but not in set A.
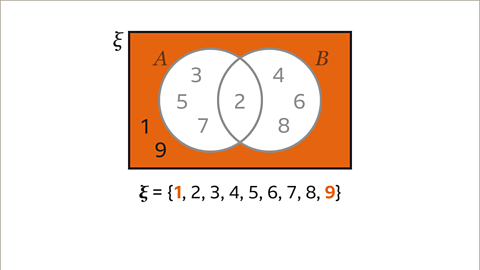
Image caption, Write any remaining elements from the universal set in the space inside the rectangle and outside the circles. The only numbers that have not yet been entered are 1 and 9, they are the odd numbers that are not prime. 1 and 9 are in the universal set but not in either set A or set B.
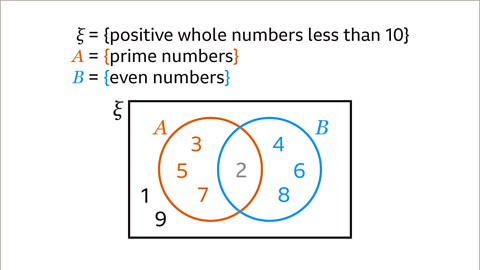
Image caption, The Venn diagram shows the prime numbers and even numbers within the universal set of positive whole numbers less than 10

Image caption, Find the mistake that has been made in this Venn diagram.
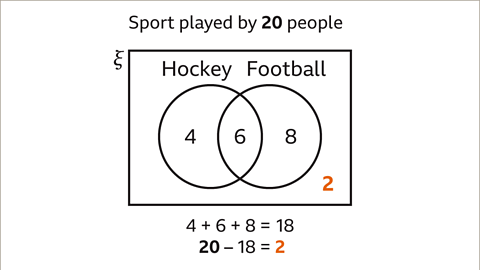
Image caption, Sport is played by 20 people. 4 + 6 + 8 = 18, the Venn diagram only shows the data of 18 people. Assuming that the given data is correct, there should be 2 people placed inside the rectangle and outside the circles who do not play either hockey or football.
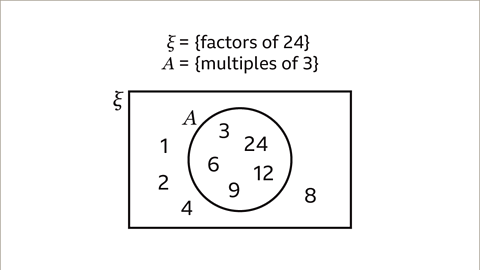
Image caption, Find the mistake that has been made in this Venn diagram.
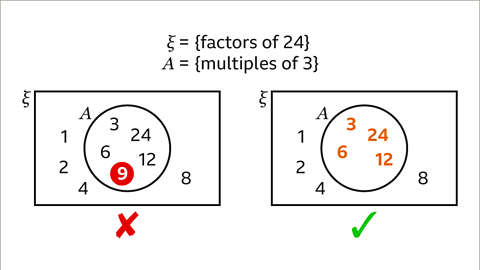
Image caption, Set A will only contain the multiples of 3 given in the universal set. This limits the multiples of 3 to 3, 6, 12 and 24 only. 9 is incorrect because it is not a factor of 24
1 of 10
Question
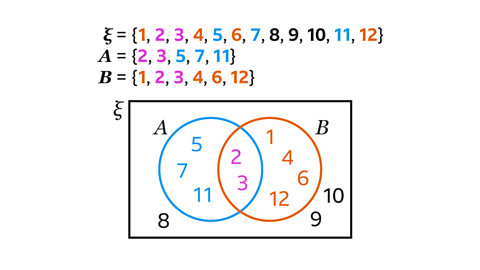
Draw a Venn diagram to show the following data:
ξ = {whole numbers from 1 to 12 inclusive}
A = {prime numbers}
B = {factors of 12}
Write each set as a list of its elements:
ξ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12}
A = {2, 3, 5, 7, 11}
B = {1, 2, 3, 4, 6, 12}Draw two overlapping circles, one for set A and one for set B, inside a rectangle for the universal set.
Fill in the overlap of the two circles with the elements that are in both set A and set B. This region is the intersection of set A and set B and contains the numbers 2 and 3. A∩B = {2, 3}.
Complete set A using the numbers 5, 7 and 11. These numbers are in set A but not in set B.
Complete set B using the numbers 1, 4, 6 and 12. These numbers are in set B but not in set A.
Complete the Venn diagram by writing the remaining numbers 8, 9, and 10 in the region that is outside the circles and inside the rectangle. These are the numbers that are not in set A or set B but are in the universal set.
The Venn diagram is now complete.
Practise understanding and interpreting Venn diagrams
Practise understanding and interpreting Venn diagrams with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths
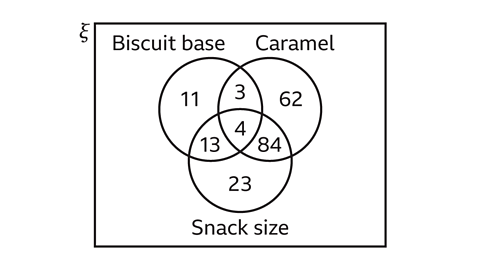
A chocolate snack manufacturer may research the features that consumers favour when creating a new product, such as:
- a biscuit base
- inclusion of nougat, fruit or caramel
- the snack size
- whether it is low calorie or contains artificial colours
The manufacturer will look for the combination of features that will give a product the highest chance of success when competing with other similar products.
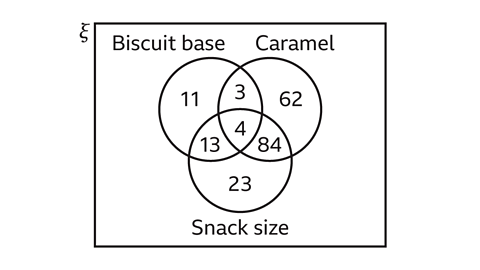
In this Venn diagram of market research, the responses collected suggest that inclusion of caramel and the size of the snack are the most favoured features of the new product. As a result, the manufacturer can focus on developing this for their target consumers.
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Sets and Venn diagrams
Find out more by working through a topic
- count2 of 5
- count3 of 5
- count4 of 5
- count5 of 5