Да ли је 50 година стар математички проблем могао да спасе Лувр од пљачке

Аутор фотографије, REUTERS/Abdul Saboor
- Аутор, Кит Јејтс
- Време читања: 8 мин
После смеле крађе у Лувру, лопови су усред бела дана успели да побегну са непроцењивим крунским накитом - ево како деценијама стар геометријски проблем може да помогне музејима да унапреде обезбеђење.
Требало им је свега осам минута.
За тих 480 секунди, лопови су се попели уз механичку платформу да би стигли до балкона на првом спрату музеја Лувр у Паризу, да би потом упали кроз изрезани прозор усред бела дана.
Кад су ушли, провалили су две стаклене витрине, а потом побегли са осам примерака непроцењивог крунског накита тиз времена Наполеона.
Била је то „смела крађа" која је потресла Француску до сржи.
До сада је ухапшено седморо осумњичених у вези са овом крађом.
ОВДЕ погледајте графички приказ велике пљачке Лувра која је запрепастила Француску.
Једно од честих питања без одговора које мучи истражитеље било је зашто лопови нису били откривени раније.
На саслушању пред Француским сенатом непосредно после пљачке, Лоранс де Карс, директорка светски славног музеја, признала је да „нису успели да заштите" крунски накит.
Једина камера која је покривала балкон на који су лопови ушли, наставила је, била је уперена у погрешном правцу, а прелиминарни извештај је открио да свака трећа просторија у крилу Денон на коју су лопови ударили није имала сигурносне камере.
Генералније гледано, Де Карс је признала да су смањења броја припадника обезбеђења учинила музеј рањивијим и инсистирала на томе да сигурносни систем Лувра мора да се појача тако да може да се „мотри" свака тачка.
Аларми у музеју су се наводно огласили кад је требало, према француском Министарству за културу.
Погледајте како су лопови побегли из Лувра после пљачке
Опет, ово је трећа крађа у француским музејима за два месеца, што је натерало Министарство да спроведе нове планове обезбеђења широм Француске.
Иако нема никакве сумње да је савремено обезбеђивање музеја сложена и скупа работа, постоји интригантан 50-годишњи математички проблем који се бави управо овим проблемом.
Он се пита који је минимални број чувара - или, еквивалентно, сигурносних камера са распоном од 360 степени - неопходан да би се читав музеј држао под присмотром?
Ово је познато као проблем музеја, или проблем ликовне галерије.
Решење је веома елегантно.

Аутор фотографије, REUTERS/Abdul Saboor
Претпоставићемо да су сви зидови нашег имагинарног музеја правих линија тако да је тлоцрт оно што математичари зову полигоном, облик са оштрим ивицама и угловима.
Камере морају да буду на фиксним положајима, али могу да виде у свим правцима.
Да бисмо били сигурни да је покривен читав музеј, морали бисмо да можемо да повучемо праву линију из било које тачке на тлоцрту до најмање једне од камера.
Узмите на пример галерију хексагоналног облика лево на дијаграму испод.
Без обзира на то где поставите камеру, моћи ћете да видите читав спрат и зидове читавог простора.
Кад на овај начин сваки положај може да се види из сваког другог, ми облик галерије називамо конвексним полигоном.
Галерија у облику слова Л у средини је неконвексна, што значи да сте ограничени у вашем постављању камера, али и даље можемо да пронађемо тачке из којих једна камера може да види читаву галерију.
Галерији облика А-З потребне су две камере да би је покрили - увек постоје тачке које ће само једна камера промашити.
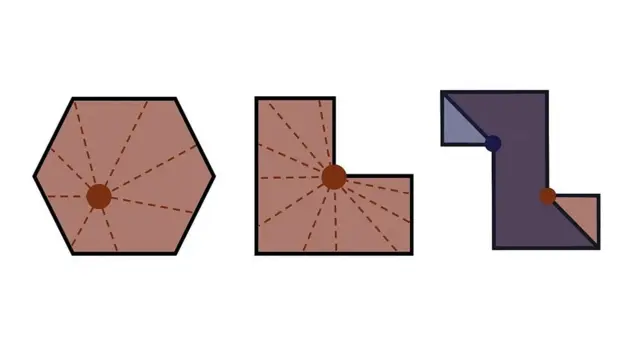
Аутор фотографије, Kit Jejts
За интересантније тлоцрте (погледајте необичан 15-странични тлоцрт испод) много је теже знати колико камера је потребно или где оне треба да стоје.
Срећом по директоре музеја ограничених музеја, чешки теоретичар графова Вацлав Хватал решио је општи проблем музеја након што је овај био постављен 1973. године.
Одговор, испоставило се, зависи од броја углова (или, како их математичари зову, „темена"), јер ће бити онолико зидова колико је углова у просторији.
Мало простог дељења помаже нам да израчунамо колико је камера потребно.
Дељењем броја углова у просторији са бројем три, сазнаћемо колико камера је потребно да она буде потпуно покривена, под претпоставком да камере имају прегледност од пуних 360 степени.
Ово функционише чак и за сложене облике као што је необична 15-страна галерија на слици испод.
У овом случају има 15 углова, дакле 15 подељено са три је пет.

Аутор фотографије, Kit Jejts
Ово функционише чак и ако број углова није дељив са три.
За галерију са 20 страна, на пример, решење је шест и две трећине.
У овим случајевима можете да узмете само цео број - дакле, не би нам било потребно више од шест камера у просторији са 20 страна.
Стив Фиск, професор математике на колеџу Боудон у Мејну, у САД, 1978. године је пронашао доказ, који се сматра једним од најелегантнијих у читавој математици, за ову нижу границу броја неопходних камера.
Његова стратегија била је да подели галерију у троуглове (погледајте леву слику фигуре испод).
Он је потом доказао да можете да изаберете само три боје - на пример, црвену, жуту и плаву - и доделите различиту боју угловима сваког троугла.
То би значило да сваки троугао у вашој галерији има различиту боју у властита три угла (погледајте десну слику фигуре испод, за пример).
То је познато као „тробојење" углова.
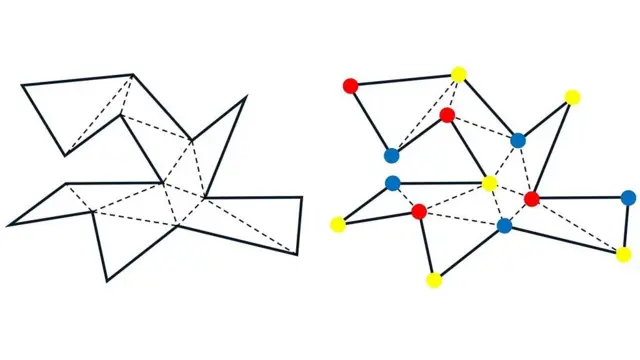
Аутор фотографије, Kit Jejts
Троуглови су једни од оних „конвексних" полигона које смо помињали раније, тако да камера постављена у било који угао (или заправо било где у троуглу) може да види сваку тачку у том облику.
Сваки троугао има углове са сваком од три боје.
То значи да можете да одаберете само једну од боја и ставите камеру на те положаје.
Те камере ће моћи да виде сваки део сваког троугла и стога сваки део галерије.
Али ево најбољег дела.
Лепота Фисковог доказа крије се у томе да можете да одаберете боју са најмање тачака, а и даље ћете покрити читаву галерију.
На облику са 15 страна изнад, бирањем црвених тачака можемо да се извучемо са само четири камере.
Штавише, црвена тачка у горњем левом углу није неопходна, зато што следећа црвена камера може да покрије читав њен простор за надзор.
Дакле, могли бисмо чак да се извучемо са три камера за ову галерију.
Ово је посебно тачно ако инсталирамо модерне камере са више праваца, уместо широкоугаоне сигурносне камере старе школе које би морале стално да пребришу простор да бисте добили потпуни преглед, привремено стварајући мртве углове.
Али не треба заборавити да многи традиционални музеји као што је Лувр имају углавном правоугаоне просторије.
Срећом, варијација на проблем ликовне галерије показује да кад се зидови спајају под одговарајућим угловима, потребна нам је само једна камера да покријемо читаву просторију.
У сведочењу, Де Карс је признала и да спољне камере Лувра не покривају све зидове.
„Нисмо приметили долазак лопова довољно рано... слабост заштите нашег периметра добро је позната", рекла је она.

Аутор фотографије, REUTERS/Gonzalo Fuentes
Срећом, постоје верзије овог проблема, познате као „проблем тврђаве" или „проблем затвора", које решавају проблем покривености камерама и за спољашњости неке грађевине.
Званичници Лувра признају да безбедносне камере нису покривале читаву спољашњост зграде
Оно што, међутим, откривају обе варијанте је да је проналажење праве тачке посматрања од кључне важности.
Али само је важно прихватити да лопови који улазе кроз јавне галерије нису једина претња са којом се суочавају музеји.
Британском музеју у Лондону, на пример, догодило се да Картијеов прстен вредан 950.000 долара нестане 2011. године из колекције која није била јавно изложена.
Драгуљи из музеја били су пронађени у огласу на иБеју 2020. године након што их је наводно узео један од кустоса музеја.

Аутор фотографије, REUTERS/Gonzalo Fuentes
Поред крађе, музеји такође морају да заштите колекције од вандализма, пожара и других облика уништавања.
Упркос томе, проблем ликовне галерије је вредан пажње чак и онима изван светих музејских простора.
Он има примену на широком дијапазону поља где су видљивост и покривеност од кључне важности.
У роботици, на пример, он помаже аутономним системима да побољшају ефикасност и спрече сударања.
У урбаном планирању, он утиче на позиционирање радио антена, торњева за пренос сигнала мобилне телефоније или детектора загађења како би осигурали свеобухватну покривеност јавних простора.
Стратегије управљања катастрофама користе сличне принципе за постављање дронова за надзор локација катастрофа широких размера из ваздуха или да би поставили пољске медицинске станице.
У монтажи покретних и компјутерских слика, проблем ликовне галерије може да помогне у идентификовању видљивих регија у оквиру неке сцене.
Он може да помогне да осигура да су глумци увек осветљени на сцени и чак помогне самим музејима да осигурају да су њихове галерије одговарајуће осветљене.
Лувр није одговорио на питања ББЦ-ја да ли је био свестан решења које нуди математички проблем музеја.
Музеј, несумњиво, тренутно има веће проблеме које мора да реши.
Али док музеји и ликовне галерије широм света преиспитују властиту сигурност после крађе у Лувру, не може да шкоди подсетити се лекција које нуди овај 50 година стар математички проблем.
Погледајте видео: Неки од драгуља украдених из Лувра
ББЦ на српском је од сада и на Јутјубу, пратите нас ОВДЕ.
Пратите нас на Фејсбуку, Твитеру, Instagramу, Јутјубу и Вајберу. Ако имате предлог теме за нас, јавите се на [email protected]
















