Key points
Division in a given ratioA part-to-part comparison. is also known as sharing in a given ratio.
Similar processes are used when dividing an amount in a ratio and finding a fraction of an amount.
To divide in a given ratio:
- bar modelOne or more rectangular bars drawn to represent information. can be used to support understanding
- a numerical method without bar models can also be used
Understanding the link between ratios and fractions is a valuable skill to practise.

Understanding the link between ratios and fractions
Examples
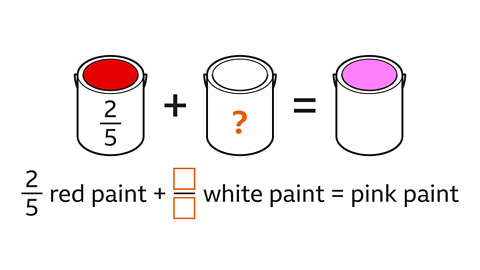
To understand the link between a ratioA part-to-part comparison. and a fraction, it is important to know that:
the ratio represents the parts that make up the whole
the total of the parts gives the denominatorNumber written on the bottom of a fraction. The denominator is the number of equal parts. Eg, for 1⁄3, the denominator is 3 of the fractions
each part of the ratio gives the numeratorNumber written at the top of a fraction. The numerator is the number of parts used. Eg, for 1⁄3, the numerator is 1 for that fractional part
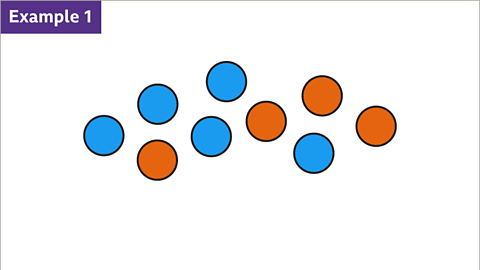
Image caption, There are nine circles. 4 circles are orange and 5 circles are blue. Find the fraction of orange circles, the fraction of blue circles and the ratio of orange to blue circles.
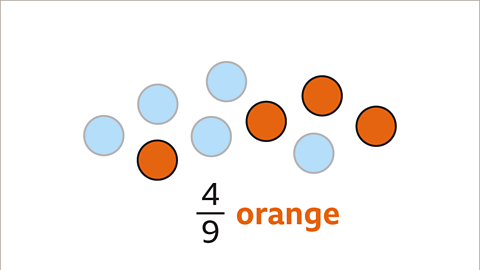
Image caption, 4 out of the 9 circles are orange. The fraction of orange circles is 4⁄9
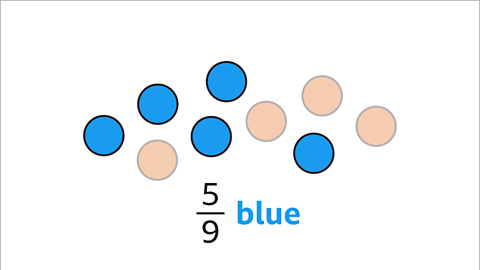
Image caption, 5 out of the 9 circles are blue. The fraction of blue circles is 5⁄9
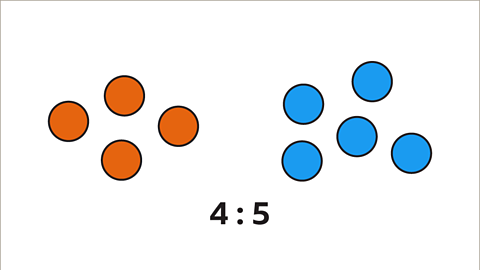
Image caption, There are 4 orange circles for every 5 blue circles. The ratio of orange circles to blue circles is therefore 4 : 5
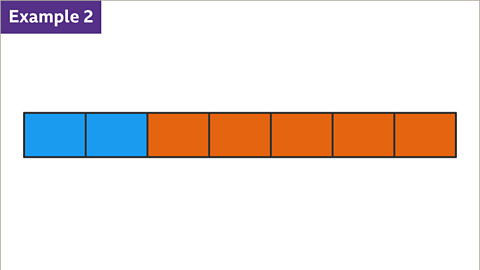
Image caption, What fraction of the bar is blue? What fraction of the bar is orange?
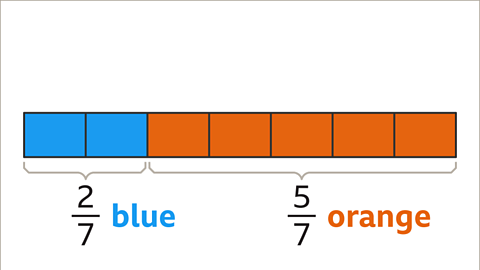
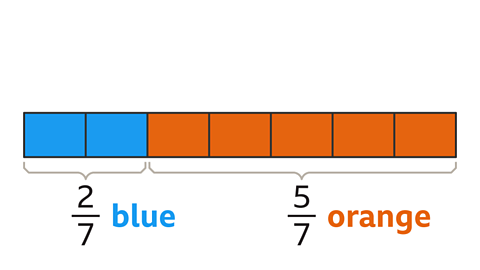
Image caption, There are 7 equal parts. 2 parts are blue. 2⁄7 of the bar is blue. 5 parts are orange. 5⁄7 of the bar is orange.
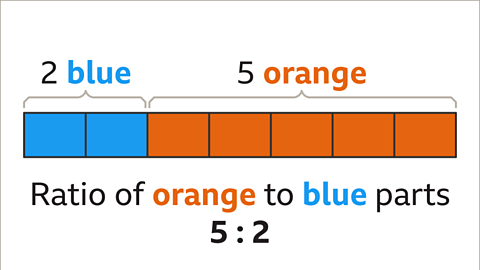
Image caption, What is the ratio of orange to blue parts? There are 5 orange parts for every 2 blue parts. The ratio of orange to blue parts is 5 : 2. The first number in the ratio is 5 because the orange parts are mentioned first. The numbers are in the same order as the description.
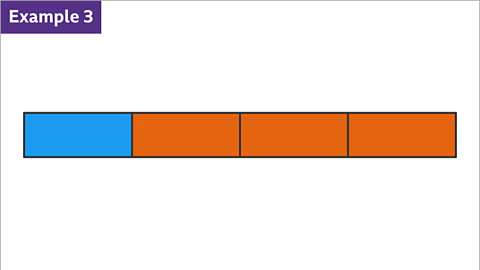
Image caption, What fraction of the bar is blue? What is the ratio of blue to orange parts?
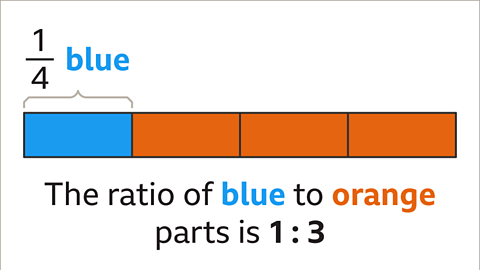
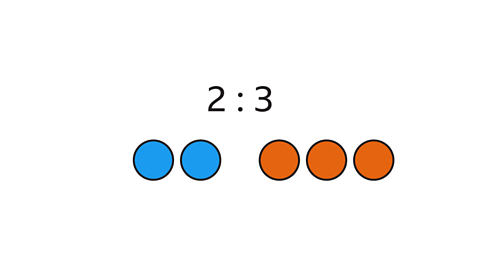
Image caption, 1 of the 4 parts is blue. ¼ of the shape is blue. There is 1 blue part for every 3 orange parts. The ratio of blue to orange parts is 1 : 3
1 of 9
Question
The ratio of the number of green to orange to blue circles is 4 : 2 : 1
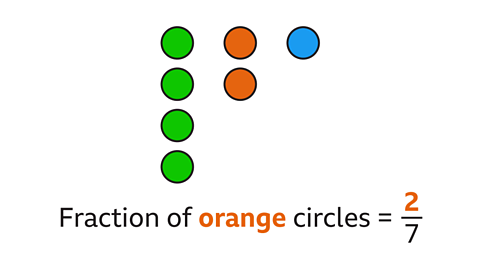
What fraction of the circles are orange?
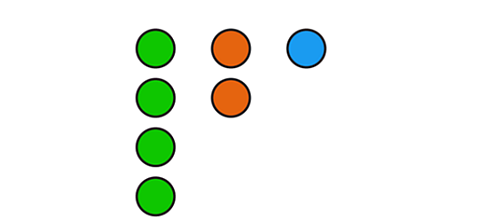
The ratio of circles is 4 : 2 : 1
The total number of parts is 7 (4 +2 + 1) - this gives the denominator of the fraction.
The ratio has 2 parts that are orange - this gives the numerator of the fraction.
The fraction of orange circles is \( \frac{2}{7} \)
Using bar models to divide in a given ratio
To divide in a ratioA part-to-part comparison. using bar modelOne or more rectangular bars drawn to represent information.:
Draw a bar modelOne or more rectangular bars drawn to represent information. to represent the whole and split it into the total number of parts.
Find the value of one part by dividing the whole by the total number of parts.
Calculate the value of each share of the ratio by multiplying the number of parts in each share of the ratio by the value of one part.
Examples
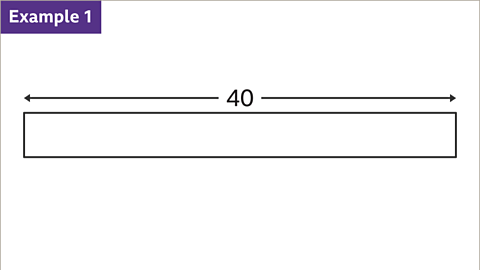
Image caption, The bar represents the whole. Divide 40 in the ratio 5 : 3
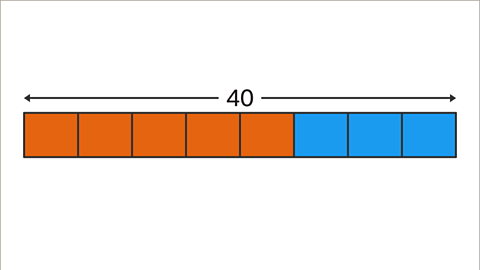
Image caption, The whole (40) is in the ratio 5 : 3. The total number of parts (5 + 3) is 8. Split the whole (40) into 8 equal parts.

Image caption, To find the value of one part, divide the whole (40) by the total number of parts (8). 40 ÷ 8 = 5. The value of one part is 5
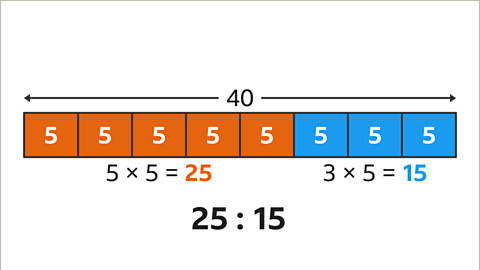
Image caption, Multiply the number of parts in each share of the ratio by the value of one part (5) - this calculates each share of 40. The first share is 5 × 5 which is 25. The second share is 3 × 5 which is 15. 40 divided in the ratio 5 : 3 is 25 : 15

Image caption, Tariq and Annie share £90 in the ratio 2 : 3. How much money do they each receive?
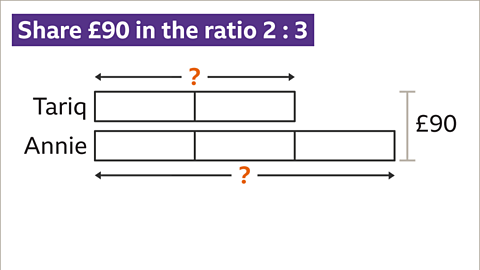
Image caption, Draw bars to represent the parts Tariq and Annie receive. Tariq will receive 2 parts and Annie will receive 3 parts. The total of the 5 parts is £90
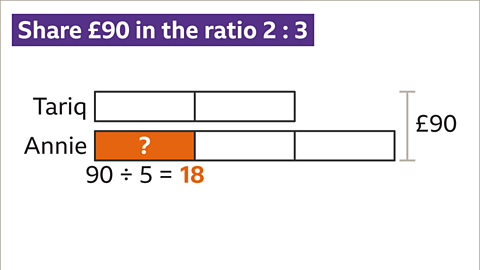
Image caption, To find the value of one part, divide the whole (90) by the total number of parts (5). 90 ÷ 5 = 18. The value of one part is 18. One part is worth £18
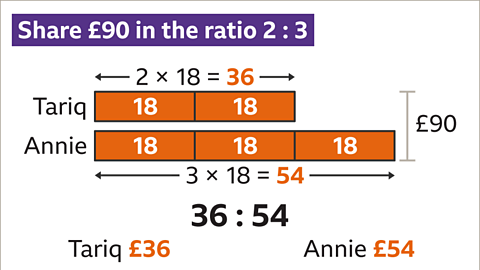
Image caption, Multiply the number of parts each person receives (2 and 3) by the value of one part (18) to calculate how much they receive. Tariq has 2 parts - he receives 2 × 18. Annie has 3 parts - she receives 3 × 18. £90 is divided between Tariq and Annie in the ratio 2 : 3. Tariq receives £36 and Annie receives £54. To check the calculation, Tariq’s and Annie’s shares should add up to £90. £36 + £54 = £90
1 of 8
Question
There are 30 dogs (German Shepherds, Golden Retrievers and Labradors) at a doggy day care centre in the ratio 1 : 5 : 4. How many Labradors are there?
Draw bars to represent the amount of German Shepherds, Golden Retrievers and Labradors.
German Shepherds are 1 part of the ratio, Golden Retrievers are 5 parts and Labradors are 4 parts.
The total number of parts in the ratio represents all 30 dogs. 1 + 5 + 4 = 10
Divide the total (30) by the total number of parts in the ratio (10) to find the number of dogs represented by one part. 30 ÷ 10 = 3
Calculate the number of Labradors by multiplying the number of parts (4) by the value of each part (3). There are 12 Labradors.
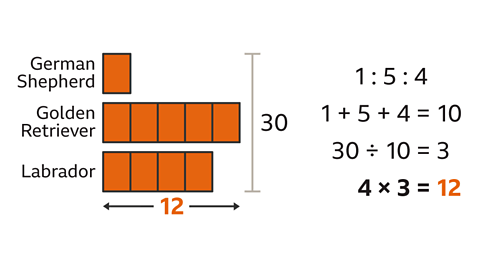
How to divide in a given ratio – numerical method
To divide an amount in a given ratioA part-to-part comparison.:
sum (verb)To add up. the parts of the ratio to get the total number of parts.
Find the value of one part by dividing the amount by the total number of parts.
Find the value of each share in the ratio by multiplying the number of parts in each share by the value of one part.
Examples

Image caption, Divide 600 in the ratio 4 : 3 : 5

Image caption, Sum the parts of the ratio. 4 + 3 + 5 = 12

Image caption, To find the value of one part, divide the amount (600) by the total number of parts (12). 600 ÷ 12 = 50. The value of one part is 50

Image caption, To find the value of each share, multiply the number of parts of each share (4, 3 and 5) by the value of one part (50). 600 shared in the ratio 4 : 3 : 5 is 200 : 150 : 250

Image caption, Dai, Jim and Kate share £300 in the ratio 8 : 5 : 2. How much money do they each receive?

Image caption, Sum the parts of the ratio (8, 5 and 2) to get the total number of parts. 8 + 5 + 2 = 15. The total number of parts is 15

Image caption, To find the value of one part, divide the amount (300) by the total number of parts (15). 300 ÷ 15 = 20. The value of each part is 20

Image caption, To find the value of each share in the ratio, multiply each ratio share (8, 5 and 2) by the value of one part (20). The calculations are 8 × 20, 5 × 20 and 2 × 20

Image caption, 8 × 20 = 160, 5 × 20 = 100 and 2 × 20 = 40. Dai, Jim and Kate share £300 in the ratio 8 : 5 : 2. Dai receives £160, Jim receives £100 and Kate receives £40
1 of 9
Question
Divide 72 in the ratio 7 : 3 : 8
Sum the parts of the ratio. 7 + 3 + 8 = 18. There are 18 parts in total.
To find the value of one part, divide the amount (72) by the total sum of the parts (18). 72 ÷ 18 = 4. The value of one part is 4
To find the value of each share in the ratio, multiply each ratio share (7, 3, 8) by the value of one part (4).
72 divided in the ratio 7 : 3 : 8 is 28 : 12 : 32

Game - Sharing ratios given a total
Complete this puzzle on sharing ratios given a total from our Divided Islands game.
Play the full Divided Islands game.
Practise division in a given ratio
Quiz
Practise division in a given ratio in this quiz. You may need a pen and paper to complete these questions.
Real-world maths
Video
Ratios are often used in jobs where liquids must be mixed in the correct proportions.
Watch the video to see how a hairdresser needs to mix a hair colour dye solution and a developer in a specific ratio to achieve a particular shade safely. The ratio can vary depending on the types of products being mixed.
Ratio proportions need to be just right when dyeing hair or a client’s hair may get damaged.
A 200 ml blend of colour and developer is required for a client. The required shade uses colour and developer in the ratio 2 : 3
200 ml is divided in the ratio 2 : 3
The hairdresser needs to mix 80 ml of colour and 120 ml of developer.
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Ratio
Find out more by working through a topic
- count3 of 5
- count4 of 5

- count5 of 5
- count1 of 5