Scale drawings - KS3 Maths

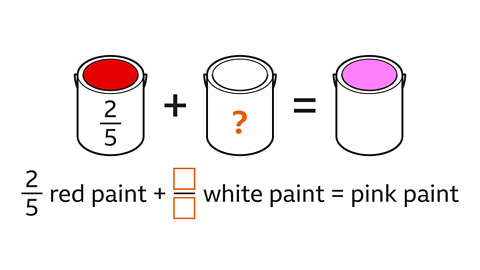
Key points

Image caption,
A scale drawing of a bridge has the same shape as the real bridge that it represents but a different size.

Scale drawings represent real objects with accurate lengths reduced or enlarged by a given .
are commonly seen as smaller representations of large objects including buildings, gardens and vehicles. Scale drawings may also be a larger representation of small objects such as parts for a watch or a medical instrument.
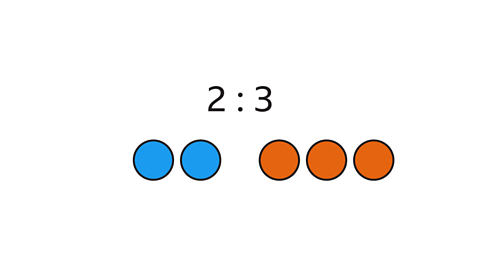
Scales are expressed in form comparing a length on a diagram to the corresponding real length. In a scale drawing, all dimensions have been reduced by the same proportion and measurements are most often in centimetres and millimetres. For example, 1 cm on a scale drawing representing 1 metre in real life is a scale of 1 : 100
When writing and using scales, understanding conversion between units, simplifying ratios and solving ratio and proportion problems can help.

Many scales are written as :

1 : n informs the user that one unit on the scale drawing represents a certain number (n) units in real life. For example, a scale of 1 : 500 means that 1 cm on the scale drawing represents 500 cm in real life.
n : 1 informs the user that a certain number (n) of units on the scale drawing represents one unit in real life. For example, a scale of 200 : 1 means that 200 mm on the scale drawing represents 1 mm in real life.

How to write a scale as a ratio

To write a scale as a ratio:

Write the length on the scale drawing first, then the corresponding length on the real object.
Convert the lengths to be in the same, smaller units.
Write the ratio without the units.
If one or both values are decimals, multiply both values by a power of ten to ensure they are both values.
Simplify the ratio by dividing both values by their .

Examples

Skip image gallery

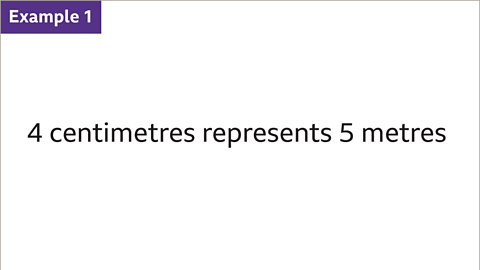
Image caption,
The scale drawing length of 4 centimetres represents the corresponding length of 5 metres on the real object. Work out the scale that has been used and write it in its simplest form.
Image caption,
Write the ratio of the length on the scale drawing first (4 centimetres), then the corresponding length of the real object (5 metres). Convert the lengths to be in the same, smaller units (centimetres). 5 metres is 500 cm.
Image caption,
Write the ratio without the units (4 : 500). Simplify the ratio by dividing both values by their HCF (4). The simplified scale is 1 : 125
Image caption,
The scale drawing length of 5 centimetres represents the corresponding length of 0∙2 millimetres on the real object. Work out the scale that has been used.
Image caption,
Write the ratio of the length on the scale drawing first (5 centimetres), then the corresponding length of the real object (0∙2 millimetres). Convert the lengths to be in the same, smaller units (millimetres). 5 cm is 50 millimetres.
Image caption,
Write the ratio without the units (50 : 0∙2). One value is a decimal (0∙2). Multiply both values by a power of ten (10) to ensure they are both integer values. The ratio is now 500 : 2. This can be simplified.
Image caption,
Simplify the ratio 500 : 2 by dividing both values by their HCF (2). The simplified scale is 250 : 1

Question

Write the scale of 5 centimetres represents 12 metres as a ratio in its simplest form.

Using a scale to find measurements for a scale drawing

To find the lengths on a scale diagram that is smaller than the real object:

Write the scale as a unitary ratio in the form 1 : n.
Convert each real length to centimetres.
Divide each real length by the scale (n).

To find the lengths on a scale diagram that is larger than the real object:

Write the scale as a unitary ratio in the form n : 1
Multiply each real length by the scale (n).
Convert each real length to centimetres, if appropriate.

Examples

Skip image gallery

Image caption,
Use a scale of 1 : 20 to find the measurements for a scale drawing of a bedroom. The floorplan of the bedroom measures 3∙4 metres by 2∙7 metres.
Image caption,
The scale 1 : 20 means that one centimetre on the scale drawing represents 20 cm in real life. The drawn length multiplied by 20 gives the real length. The real length divided by 20 gives the drawn length. To find the scale drawing measurements for this example, the real lengths will be divided by 20
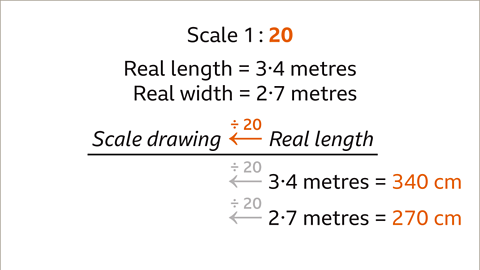
Image caption,
The scale 1 : 20 is a unitary ratio. Each real length divided by 20 gives the scaled length. Convert each real length to centimetres to make the division easier. 3∙4 metres is 340 cm. 2∙7 metres is 270 cm.
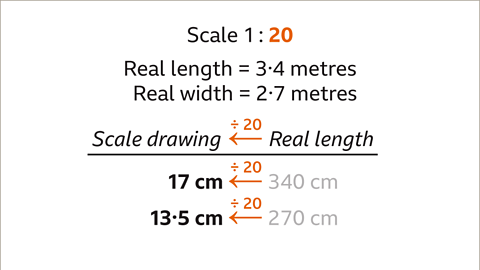
Image caption,
Divide each real measurement by the scale. 340 ÷ 20 = 17. The bedroom length on the scale diagram will be 17 cm. 270 ÷ 20 = 13∙5. The bedroom width on the scale diagram will be 13∙5 cm.
Image caption,
Use a scale of 15 : 2 to find the measurements for a scale drawing of a machine component. The real length of the component is 8 millimetres. The real width of the component is 3 millimetres.
Image caption,
Write the scale as a unitary ratio in the form n : 1 by dividing both parts of the ratio by 2. 15 ÷ 2 = 7∙5 and 2 ÷ 2 = 1. The ratio becomes 7∙5 : 1
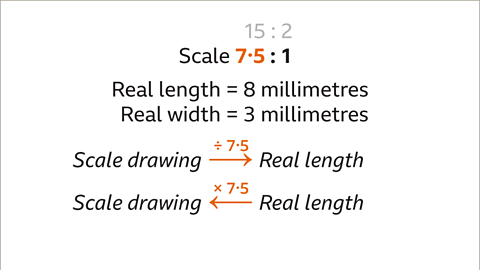
Image caption,
The scale 7∙5 : 1 is a unitary ratio in the form n : 1. 7∙5 cm on the scale drawing represents 1 cm in real life. The drawn length divided by 7∙5 gives the real length. The real length multiplied by 7∙5 gives the drawn length. The scale drawing enlarges the size of the machine component by a scale factor 7∙5
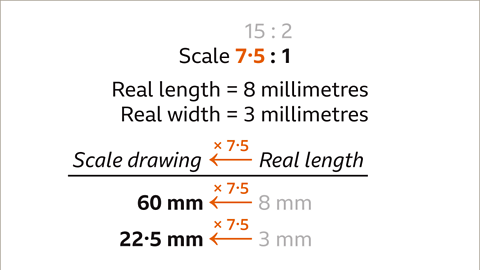
Image caption,
Multiply each real length by the scale (7∙5). 8 × 7∙5 = 60, the component length is 60 mm. 3 × 7∙5 = 22∙5, the component width is 22∙5 mm.

Question

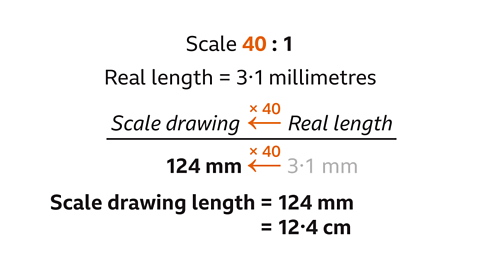
A scale drawing of a small insect is drawn using a scale of 40 : 1. What length on the drawing is used if the insect is 3∙1 millimetres long?

Using a scale to find real lengths

To find the actual lengths from a scale diagram, where the object is larger:

Write the scale as a unitary ratio in the form 1 : n.
Multiply each scaled length by the scale (n).
Convert the units, if appropriate.

To find the actual lengths from a scale diagram, where the object is smaller:

Write the scale as a unitary ratio in the form n : 1
Divide each scaled length by the scale (n).
Convert the units, if appropriate.

Examples

Skip image gallery

Image caption,
A scale drawing with the scale of 2 : 25 gives the distance between a pair of wall sockets as 25∙6 centimetres. Find the actual distance between the sockets in metres.
Image caption,
Write the scale as a unitary ratio in the form 1 : n by dividing both parts by 2. 2 ÷ 2 = 1 and 25 ÷ 2 = 12∙5. The unitary ratio is 1 : 12∙5
Image caption,
The scale 1 : 12∙5 is a unitary ratio in the form 1 : n. 1 cm on the scale drawing represents 12∙5 cm in real life. The drawn length multiplied by 12∙5 gives the real length. The scale drawing enlarges the size of the machine component by scale factor 12∙5
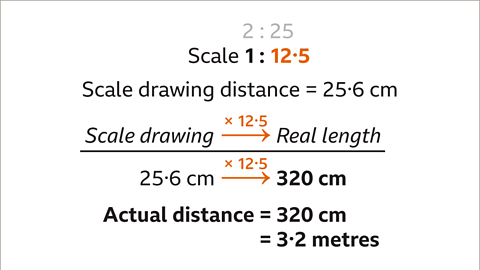
Image caption,
Multiply the scaled length (25∙6 cm) by the scale (12∙5). 25∙6 × 12∙5 = 320. The real distance between the sockets is 320 cm. This is the same as 3∙2 metres.
Image caption,
A 3D printer is programmed to produce very small components to make a model. A scale drawing with the scale of 50 : 1 gives the width of one component as 2 cm. Find the actual width of this component.
Image caption,
The scale 50 : 1 is a unitary ratio in the form n : 1. 50 cm on the scale drawing represents 1 cm in real life. The drawn length divided by 50 gives the real length. The scale drawing is larger than the component by scale factor 50
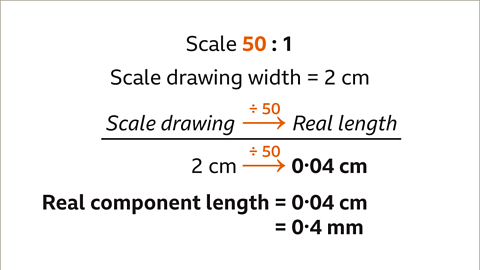
Image caption,
Divide the scaled length (2 cm) by the scale (50). 2 ÷ 50 = 0∙04. The real length of the component is 0∙04 cm. This is the same as 0∙4 millimetres.

Question

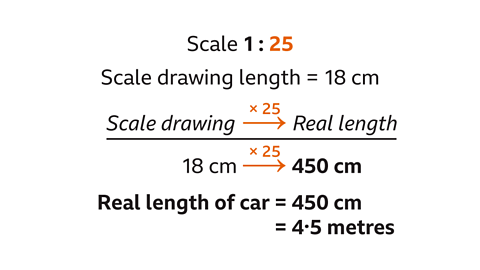
A scale drawing of a car uses the scale 1 : 25. The length of the car on the drawing is 18 cm. How long is the actual car?

Practise using scale drawings

Quiz

Practise using scale drawings in this quiz. You may need a pen and paper to complete these questions.

Real-world maths

Image caption,
In this scale drawing of a car, all dimensions have been reduced by the same proportion.

Scale drawings are used by designers to plan and adjust details before actual production so that all problems can be addressed.

CAD (computer- aided design) relies heavily on scaling software, interpreted by automotive, structural and civil engineers. A scale drawing of a car has the same shape as the real car that it represents but a different size.

People searching for a house to buy can access floorplans of properties and see a scale drawing that enables them to get a feel for the layout of the house. They may plan what furniture to buy that will fit in each room.