Solving ratio problems - KS3 Maths

Key points

problems take different forms, which may include:
- linking ratios and
- part-part problems - where the value of one part of the ratio is given and the value of another ratio part has to be found
- part-whole problems - where the value of one part of the ratio is given and the value of the whole has to be found
- comparison problems - where the ratio and the difference between the values is given
- problems where values change, giving a new ratio
In order to solve ratio problems, an understanding of the structure of the problem is needed. A may help to clarify this.
An understanding of equivalent ratios and simplifying ratios, as well as division in a given ratio is needed to solve ratio problems.

Solving problems involving ratios and fractions

To solve a problem involving ratios and fractions, you may be given the or the .

When given the ratio:

Add the ratio parts together to find the of the fraction.
The of the fraction is the ratio part that is the focus of the question.

When given the fraction:

The numerator of the fraction gives one of the ratio parts.
Find the other ratio part by subtracting the numerator from the denominator.
Write the ratio in the correct order.

Examples

Skip image gallery

Image caption,
The ratio of horses to donkeys at an animal sanctuary is 5 : 2. What fraction of the animals are donkeys?
Image caption,
Add the ratio parts (5 and 2) to find the denominator of the fraction. 5 + 2 = 7. The denominator is 7
$The same information. Donkeys and two from the ratios are highlighted. The fraction is now two sevenths – two is highlighted.$
Image caption,
The numerator of the fraction is the ratio part that is the focus of the question (donkeys). The numerator is 2. The fraction of the animals that are donkeys is 2⁄7
$Example 2 – Given the fraction: A diagram showing a can of red paint labelled two fifths plus a can of white paint labelled with a highlighted question mark equals a can of pink paint. Written below: Two fifths red paint plus a blank fraction, with highlighted boxes, white paint equals pink paint.$
Image caption,
To make pink paint, 2⁄5 red paint is mixed with white paint. How much white paint is needed? What is the ratio of red to white paint?
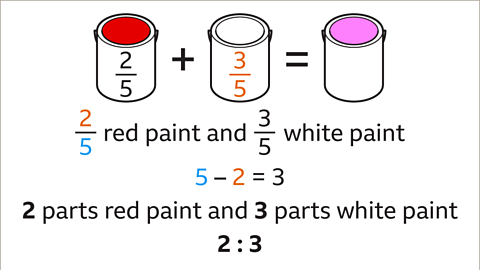
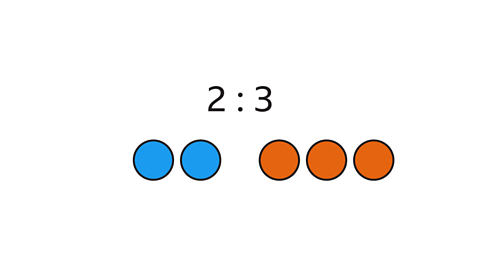
Image caption,
The numerator of the fraction of red paint is 2. This is the ratio part for red paint. To find the ratio part for the white paint, subtract the numerator from the denominator. 5 – 2 = 3. The ratio part for white paint is 3. 3⁄5 of the paint is white. The ratio of red to white paint is 2 : 3

Question

A farm has sheep and goats in the ratio 7 : 5 (sheep : goats). What fraction of the animals are sheep?

Solving part-part and part-whole ratio problems

A part-part ratio problem is where the value of one part of the ratio is given and the value of another ratio part has to be found. A part-whole problem is where the value of one part of the ratio is given and the value of the whole has to be found.

Given a ratio and the value of one part of the ratio, find the value of another ratio part or the value of the whole.

Draw a split into the total number of parts. Label with the given information to represent the problem.
Find the value of one part by dividing the given value by the associated number of parts.
- To find the value of another ratio part in a part-part problem, multiply the value of one part by the number of parts asked for.
- To find the whole in a part-whole problem, multiply the value of one part by the total number of parts.

Examples

Skip image gallery

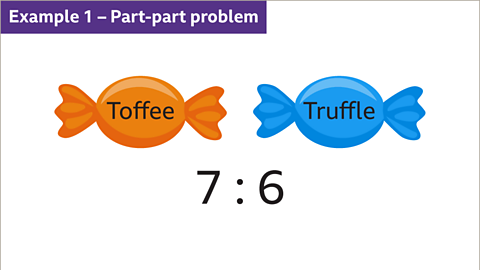
Image caption,
A box contains toffees and truffles in the ratio 7 : 6. There are 24 truffles. How many toffees are there?
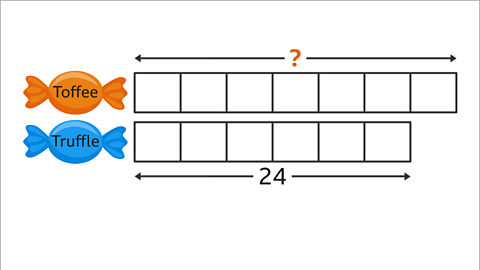
Image caption,
Draw a bar model and label it to illustrate the problem. The ratio of toffees to truffles is 7 : 6. Draw 7 parts for the toffees and 6 for the truffles. Label the truffle bar with 24. To work out the total number of toffees, the value of one part needs to be found.
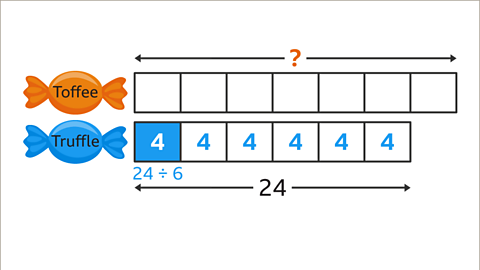
Image caption,
To work the value of one part, divide the number of truffles (24) by the number of parts given (6). This gives the value of one part. 24 ÷ 6 = 4
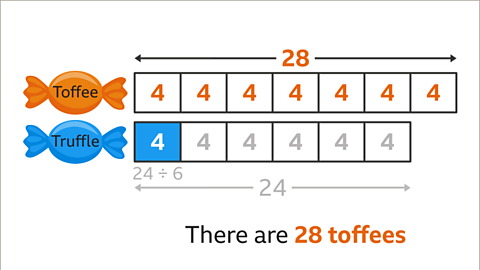
Image caption,
Multiply the value of one part (4) by the number of parts asked for: the toffees (7). 4 × 7 = 28. There are 28 toffees in the box.
Image caption,
A library stocks books for children and books for adults in the ratio 3 : 5. There are 450 books for children. How many books are in the library?
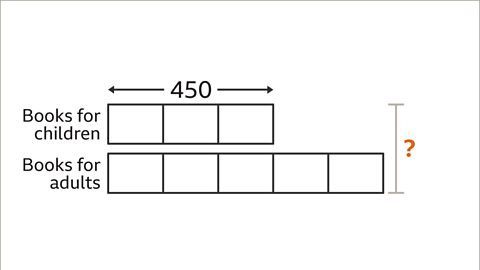
Image caption,
Draw a bar model and label it to illustrate the problem. The ratio of books for children to books for adults is 3 : 5. Draw 3 parts for books for children and 5 parts for books for adults. Label the books for children bar with 450. To work out the total number of books, the value of one part needs to be found.
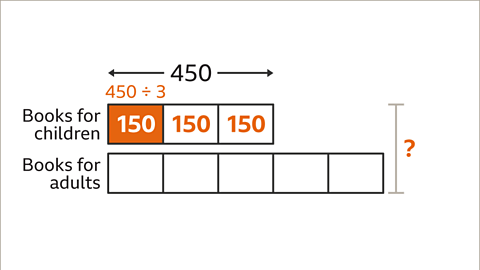
Image caption,
To find the value of one part, divide the amount of books for children (450) by the number of parts given (3). 450 ÷ 3 = 150. The value of one part is 150
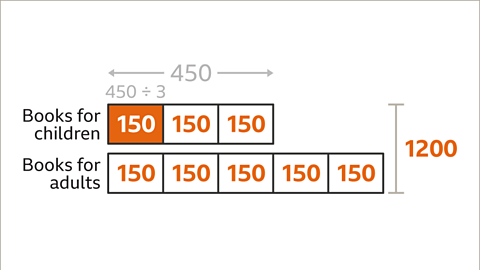
Image caption,
Multiply the value of one part (150) by the number of parts asked for: the number of books in the library. This is the total of books for children parts and the books for adults parts. (3 + 5 = 8). The calculation is 150 × 8. The total number of books in the library is 1200.

Question

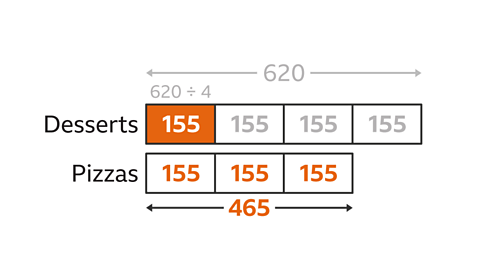
The ratio of desserts to pizzas in a supermarket freezer is 4 : 3
There are a total of 620 desserts.
How many pizzas are in the freezer?

Solving ratio problems involving comparisons

Some ratio problems involve a comparison between values. The comparison is the value difference between two parts of the ratio.

Given a ratio and a comparison between values:

Draw a bar model to illustrate the problem.
Label the given information.
Find the value of one part by dividing the comparison value by the number of parts given.
Multiply the value of one part by the number of parts of the object of the question.

Examples

Skip image gallery

Image caption,
Everyone at a fancy dress party is dressed up as either a vampire or a wizard. The ratio of people dressed as vampires to wizards is 5 : 2. If there are 6 more vampires than wizards, how many people are at the party?
Image caption,
Draw a bar model to illustrate the problem. The ratio of vampires to wizards is 5 : 2. There are 5 parts for the vampires and 2 parts for the wizards.
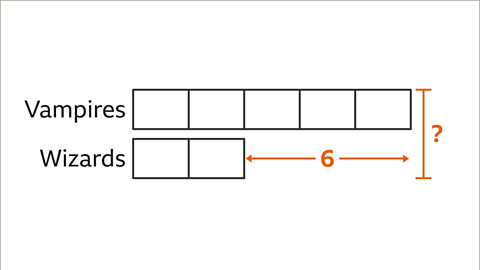
Image caption,
Label the given information. There are 6 more vampires than wizards. The diagram shows the comparison between the vampires bar and the wizards bar. To work out the total number of people at the party, the value of one part needs to be found.
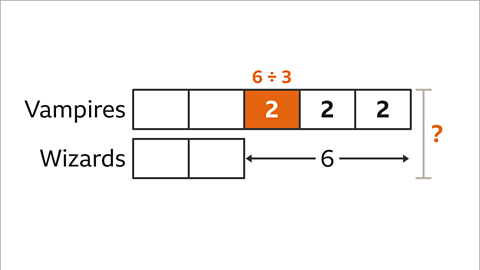
Image caption,
To find the value of one part, divide the difference value (6) by the number of parts that make up the difference (3). 6 ÷ 3 = 2. The value of one part is 2
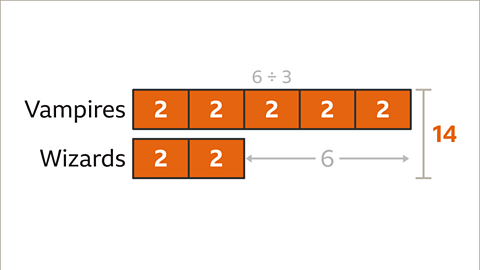
Image caption,
Multiply the value of one part (2) by the number of parts asked for (all the people so all the parts, 7). 2 × 7 = 14. The total number of people at the party is 14
Image caption,
The ratio of the number of tulips to daffodils in a flower display is 3 : 7. There are 96 fewer tulips than daffodils. Find the number of daffodils in the display.
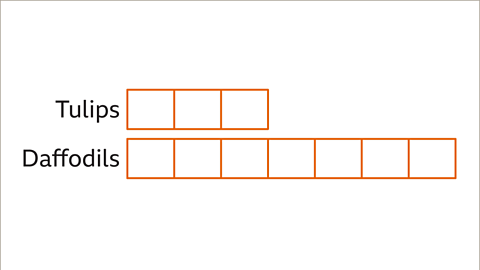
Image caption,
Draw a bar model to illustrate the problem. The ratio of tulips to daffodils is 3 : 7. There are 3 parts for tulips and 7 parts for daffodils.
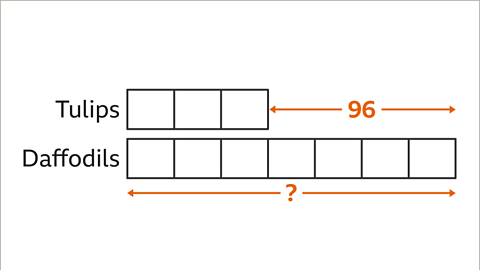
Image caption,
Label the given information. There are 96 fewer tulips than daffodils. The diagram shoes the comparison between the tulips bar and the daffodils bar. To work out the number of daffodils in the display, the value of one part needs to be found.
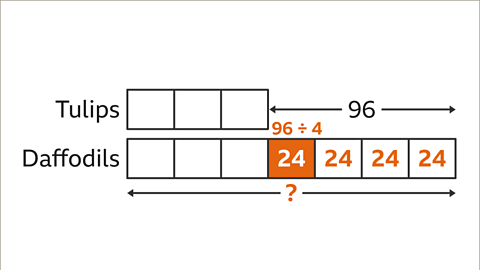
Image caption,
To find the value of one part, divide the comparison value (96) by the number of parts that make up the difference (4). 96 ÷ 4 = 24. The value of one part is 24
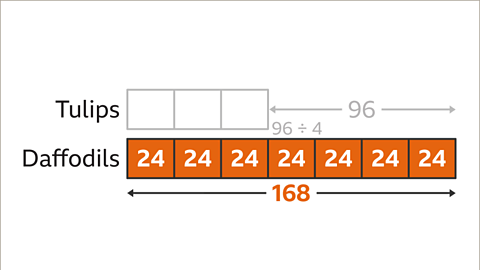
Image caption,
Multiply the value of one part (24) by the number of parts asked for (all the daffodils, 7 parts). 24 × 7 = 168. The number of daffodils in the display is 168

Question

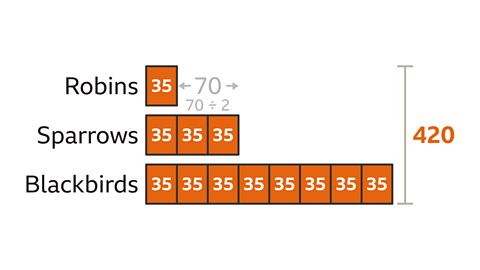
The ratio of the number of robins to sparrows to blackbirds in a survey of garden birds is 1 : 3 : 8 (robins : sparrows : blackbirds)

There were 70 fewer robins than sparrows. How many birds were observed in this survey?

Solving ratio problems with changing amounts

Given a ratio and total amount, find the new changing amounts and find the new ratio:

A total amount and ratio is given. Draw a bar model to illustrate this starting information.
Divide the total amount in the initial ratio.
- Find the value of one part by dividing the total amount by the sum of the parts.
- Multiply the value of one part by the number of parts for each share of the ratio.
Adjust the shared amounts according to the given information in the question.
Write the new amounts as a ratio and simplify, if necessary, by dividing the parts by their (HCF).

In this example, you need to be able to divide in a given ratio and simplify ratios.

Example

Skip image gallery

Image caption,
A market stall has 60 T-shirts. The ratio of small, medium and large T-shirts being sold on the stall is 2 : 3 : 1. The stallholder sells 26 medium and 2 large T-shirts. What is the ratio of small, medium and large T-shirts now?
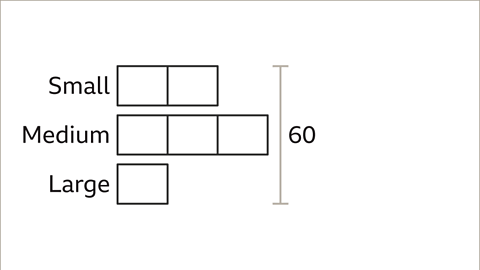
Image caption,
Draw a bar model to illustrate the starting information. Draw 2 parts for small T-shirts, 3 for medium and 1 for large. The total number of T-shirts is 60
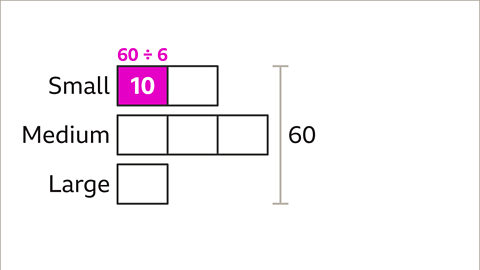
Image caption,
Divide 60 in the ratio 2 : 3 : 1. To find the value of one part, divide the total number (60) by the sum of the parts (2 + 3 + 1 = 6). 60 ÷ 6 = 10. The value of one part is 10
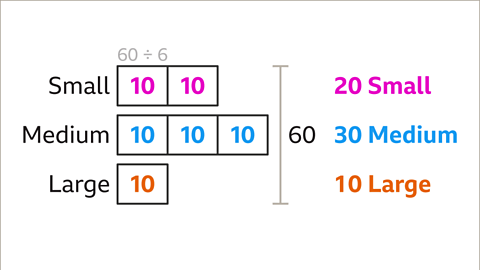
Image caption,
2 parts are small, so 2 × 10 = 20 small T-shirts. 3 parts are medium, so 3 × 10 = 30 medium T-shirts. 1 part is large, so 1 × 10 = 10 large T-shirts.
Image caption,
Adjust the shared amounts according to the given information in the question. At the start there were 20 small, 30 medium and 10 large T-shirts. 26 medium and 2 large T-shirts are sold. The remaining T-shirts are 20 small, 4 medium and 8 large T-shirts.
Image caption,
The ratio of small to medium to large T-shirts is now 20 : 4 : 8. This ratio can be simplified.
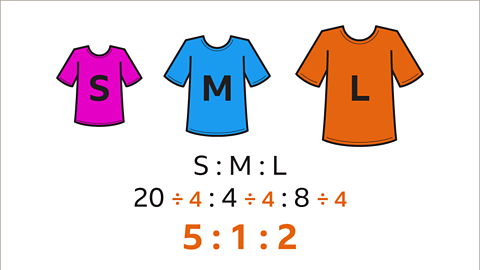
Image caption,
To simplify the ratio, divide each part by their highest common factor (HCF). The HCF of 20, 4 and 8 is 4. Divide each part by 4. The new simplified ratio of small to medium to large T-shirts is 5 : 1 : 2

Question

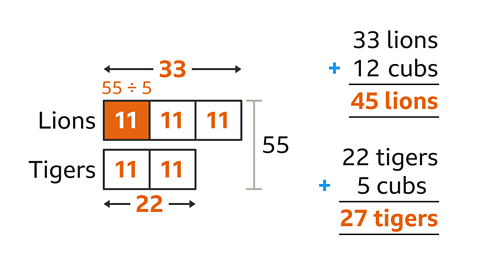
There are 55 big cats in a safari park.
The ratio of lions to tigers is 3 : 2
12 lion cubs and 5 tiger cubs are born. What is the ratio of lions to tigers now?

Game - Comparing ratios, fractions and percentages

Try out these comparing ratios, fractions and percentages puzzles from our maths game Divided Islands.

Play the full Divided Islands game.

Practise solving ratio problems

Quiz

Practise solving ratio problems in this quiz. You may need a pen and paper to complete these questions.

Real-world maths

Image caption,
A baker will use a ratio of 2 parts sugar to 1 part egg white to make meringues.

Ratio problems occur in many different contexts.

Successful cookery relies on the ratio of the ingredients used. For example:
- To make meringues, you need a ratio of 2 parts sugar to 1 part egg white.
- To make Yorkshire puddings, you need equal amounts of egg, flour and milk (and a pinch of salt). The ratio of egg, flour and milk is 1 : 1 : 1
In construction, fencing companies use a fixed ratio of concrete mix to water to secure fence posts. For a given amount of concrete mix, the amount of water needed is worked out. This is a part-to-part ratio problem.