Inverse proportion - KS3 Maths

Key points

Two males and one female dressed in black polo shirts painting and decorating a pink wall — Image caption,
More decorators working on a job would reduce the time to complete the task. They are inversely proportional.

If two quantities are inversely proportional, one increases as the other decreases at the same rate. If one quantity doubles, the other one halves. For example, more workers on a job would reduce the time to complete the task. They are inversely proportional.
is written using the . For example, if two \(x\) and \(y\) are inversely proportional to each other, then this statement can be represented as \(x\) ∝ \( \frac{1}{y} \)
When the proportionality symbol (∝) is replaced with an equals sign (=), the equation is \(x = k y\). The constant value (often written as \(k\)) relates to the amounts that increase or decrease at the same rate.
Inverse proportion problems can be solved by using the . This is the fixed product of each pair of variables. The constant of proportionality is divided by the known quantity to find the missing quantity.

How to decide whether two variables are inversely proportional

To decide if two are inversely proportional, check for the following:

As one quantity increases, the other quantity decreases in the same proportion.
As one quantity decreases, the other quantity increases in the same proportion.
The quantities have a fixed . This is known as the .

Examples

Skip image gallery

Image caption,
Explain why the width and length of rectangles with a fixed area of 12 cm² are inversely proportional.
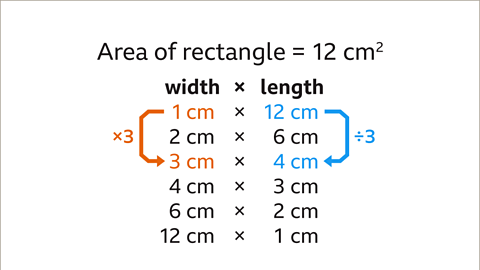
Image caption,
Two quantities are inversely proportional when one quantity increases and the other quantity decreases in the same proportion. This is true for all the widths and lengths of a fixed area of 12 cm². For example, as the width is multiplied by 3, the length is divided by 3 The width and length of rectangles with a fixed area are inversely proportional.
Image caption,
Two quantities are inversely proportional if the quantities have a fixed product. The table shows that the width multiplied by the length is always 12 cm² . The width and length of rectangles with a fixed area are inversely proportional. The fixed area (12cm² ) is the constant of proportionality.
Image caption,
An equation can be written connecting the width and the length.
Image caption,
Explain why the width and length of rectangles with a fixed perimeter of 12 cm are not inversely proportional.
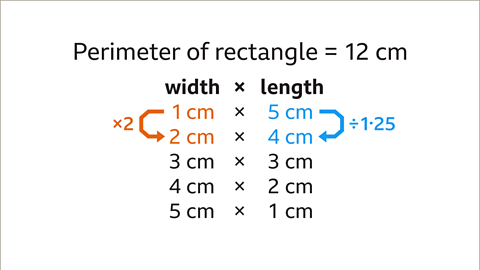
Image caption,
Two quantities are inversely proportional when one quantity increases and the other quantity decreases in the same proportion. This is not true for all the widths and lengths of a fixed perimeter of 12 cm. For example, when the width 1 cm doubles to 2 cm, the length goes from 5 cm to 4 cm. This is divided by 1۰25, not halved. The width and length of rectangles with a fixed perimeter are not inversely proportional.
Image caption,
Two quantities are inversely proportional if the quantities have a fixed product. This means every pair of values must give the same product to be inversely proportional, but they do not. The width and length of rectangles with a fixed perimeter are not inversely proportional.

Question

Explain why the amount of fuel in a tank and the amount of fuel used are not inversely proportional.

A diagram of a table with two rows and five columns. First row: Fuel in tank open brackets litres close brackets. Twenty-five. Twenty. Ten. Five. Second row: Fuel in tank open brackets litres close brackets. Five. Ten. Twenty. Twenty-five.

Solving inverse proportion problems using multiplicative reasoning

involves using multiplication and division to find other values. To use this method:

Look for multiplicative links. Find a multiplication relationship (number of times greater) or division relationship (number of times smaller).
Repeat the same multiplication or division on the other .

Examples

Skip image gallery

Image caption,
The number of builders and the time they take to build houses are inversely proportional. It takes 15 builders 12 months to build the houses. How long would it take 5 builders to build the houses?
Image caption,
The number of builders and the time they take to build some houses are inversely proportional. The variables are the number of builders and the time they take. The fewer builders there are, the more time is taken. The number of builders is divided by three (15 ÷ 3 = 5). The inverse of dividing by three is multiplying by three. The time taken is multiplied by three (12 × 3 = 36). It will take 5 builders 36 months (3 years) to build the houses.
Image caption,
The faster the speed, the less time a journey takes. The speed and the time taken are inversely proportional. At an average speed of 30 mph the journey takes 4½ hours. What speed will be necessary to complete the journey in 2¼ hours?
Image caption,
The speed and the time taken are inversely proportional. The variables are the speed and the time taken. The shorter the time taken, the faster the speed. The time taken has been halved (4½ ÷ 2 = 2¼). The inverse of halving is doubling. The speed is doubled (30 × 2 = 60). To complete the journey in 2¼ hours the speed is 60 mph.

Question

5 workers would take 108 hours to complete a job. The firm wants to complete the job in a shorter time. How long will the job take to complete if they have 9 workers?

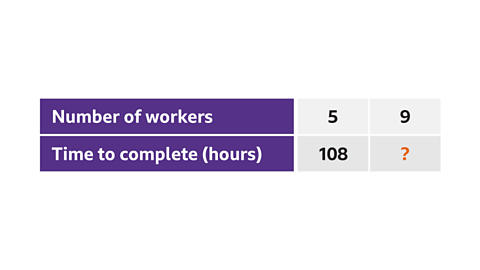
A diagram of a table with two rows and three columns. First row: Number of workers. Five. Nine. Second row: Time to completion open brackets hours close brackets. One-hundred and eight. A question mark – highlighted.

Solving inverse proportion problems: constant of proportionality

problems can be solved by using the . This is the fixed product of each pair of variables.

Constant of proportionality method:

Find the value of the constant of proportionality by multiplying a given pair of variables.
Divide the constant of proportionality by the known quantity to find the missing quantity.

Examples

Skip image gallery

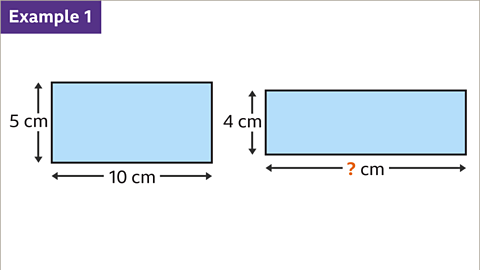
Image caption,
The rectangles have equal areas. The width and length of rectangles with equal areas are inversely proportional. Find the missing length.
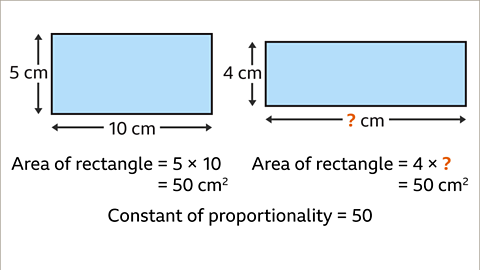
Image caption,
Find the constant of proportionality by multiplying a given pair of variables (5 and 10). The constant of proportionality is the product of the width (5) and length (10), which gives the area of the rectangle. 5 × 10 = 50 The area of the rectangle is 50 cm². The constant of proportionality is 50
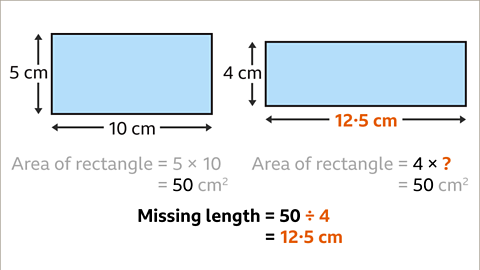
Image caption,
Divide the constant of proportionality (50) by the known quantity (4) to find the missing quantity. 50 ÷ 4 = 12∙5 The missing length is 12∙5 cm.
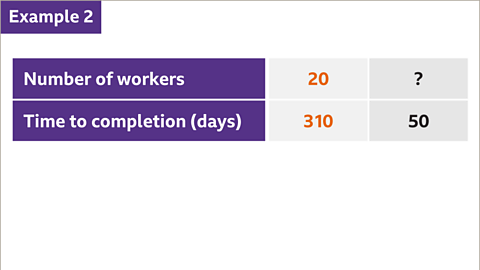
Image caption,
The number of workers and the time it takes to complete a project are inversely proportional. The project manager knows that with 20 workers, the project will take 310 days. However, the client wants the project completed in 50 days. Find the number of workers required to complete the project in 50 days.
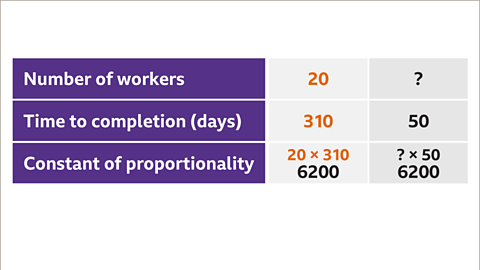
Image caption,
Find the constant of proportionality by multiplying the given pair of quantities (20 and 310). The product of the number of workers (20) and the time taken (310) gives the constant of proportionality. 20 × 310 = 6200 The constant of proportionality for the project is 6200, which is the total number of days it will take for the workers to complete the job.
Image caption,
Divide the constant of proportionality (6200) by the known quantity (50) to find the missing quantity. 6200 ÷ 50 = 124 There needs to be 124 workers to complete the project in 50 days.

Question

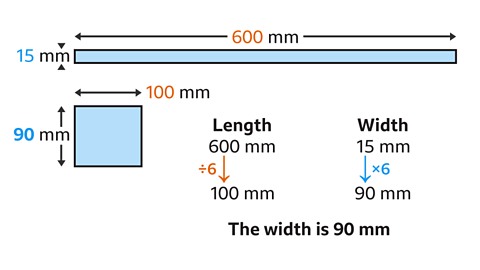
Two rectangles have equal areas. The width of the rectangles are inversely proportional to their lengths. Given that one rectangle measures 600 mm by 15 mm and the second rectangle has one side length of 100 mm, find the width of its other side.

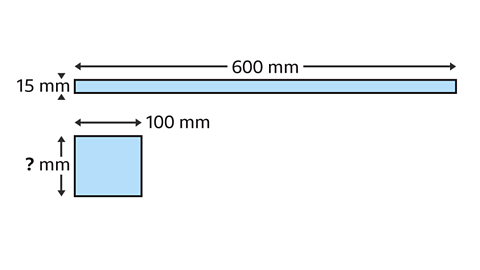
A diagram showing two rectangles. First rectangle: The left is labelled fifteen millimetres with arrows pointing to the top and bottom. The top in labelled six-hundred millimetres with arrows pointing to each end. Second rectangle: The left is labelled with a question mark millimetres with arrows pointing to the top and bottom. The top in labelled one-hundred millimetres with arrows pointing to each end.

Practise ratio and inverse proportion

Practise ratio and inverse proportion with this quiz. You may need a pen and paper to help you work things out.

Quiz

Real-world maths

Image caption,
Construction companies may use inverse proportion: more builders means faster completion.

Inverse proportion may be used by a construction company. The more builders, the faster a building project will be completed.

More workers also means more costs, but when a builder has to meet a set deadline they will employ more people to complete the job on time. This is so that they do not have to pay a penalty for completing the job late.