KS3

How to draw direct and inverse proportion graphs

Part ofMathsDirect and inverse proportion

Key points

Image caption,
This graph shows that the cost of cheese (𝒚) is directly proportional to the amount of cheese (𝒙).

is where the variables move in the same direction and by the same proportion. As one increases or decreases so does the second variable at the same rate. When the value of \(x\) is multiplied by 10, \(y\) is also multiplied by 10. When \(x\) is halved, \(y\) is also halved. So \(x∶y\) is always the same. The notation and the general equation for \(y\) being directly proportional to \(x\) is \(y=nx\).
A graph showing direct proportion is a straight line passing through the , which is the coordinate (0, 0). When \(x=\) 0, \(y=\) 0
The notation and the general equation for graphs is \(y=\frac{k}{x}\). The product of the two variables, \(x\) and \(y\), is always \(k\). For \(k=\) 20, when \(x=\) 4, then \(y=\) 5. When \(x=\) 20, then \(y=\) 1
A graph showing inverse proportion is a curve. The curve gets closer to the axes as \(x\) and \(y\) reach . As one variable increases, the second variable decreases at the same rate. When the value of \(x\) is multiplied by 10, \(y\) is divided by 10. When \(x\) is halved, \(y\) is doubled.
Graphs are drawn by plotting pairs of values \((x,y)\), named . A direct proportional graph is drawn plotting three coordinates. An inverse proportional graph requires more points to give an accurate curve.

Image caption,
This graph shows that the cost of cheese (𝒚) is directly proportional to the amount of cheese (𝒙).

How to recognise whether graphs show direct or inverse proportion

If a graph shows direct proportion:

the graph is a straight line
the line goes through the origin (0, 0)
for any coordinate \((x,y)\), \(x : y\) is constant
the equation of the line has the general form \(y=nx\)

If a graph shows inverse proportion:

the graph is a curve
the curve does not cross either axis
for any coordinate \((x,y)\), the product of \(x\) and \(y\) is always the same \((xy=k)\)
the equation of the curve has the general form \(y=\) \( \frac{k}{x}\) for each coordinate

Examples

Skip image gallery

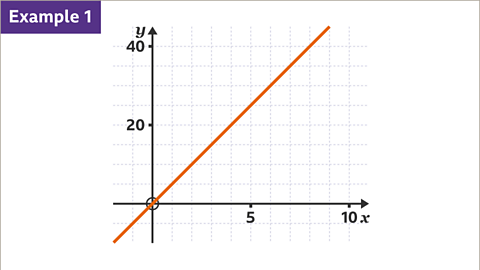
Image caption,
Explain why this graph shows direct proportion.
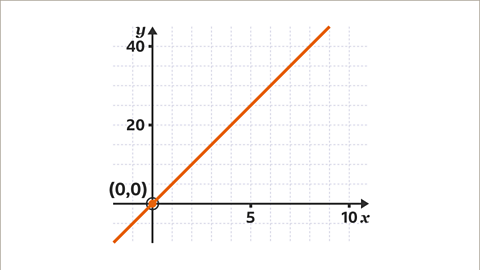
Image caption,
A graph showing direct proportion is a straight line that passes through the origin (0, 0).
Image caption,
Some of the coordinates of the graph are shown: (0, 0), (4, 20), (5, 25) and (8, 40). These points can be used to show that 𝒙 and 𝒚 are directly proportional.
Image caption,
In a graph showing direct proportion, for any coordinate (𝒙, 𝒚), 𝒙 : 𝒚 is constant. In this case 𝒙 : 𝒚 = 1 : 5. The 𝒚 value is always five times the 𝒙 value. The equation of the line is 𝒚 = 5𝒙. This is the general form of a direct proportion graph (𝒚 = n𝒙).
Image caption,
Explain why this graph shows inverse proportion.
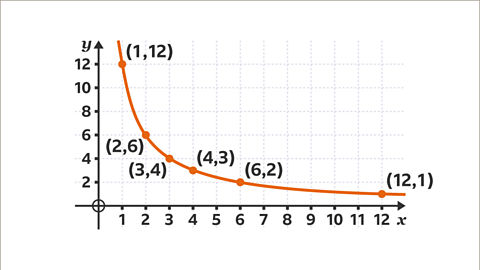
Image caption,
The graph is a curve. The curve does not touch either the 𝒙-axis or the 𝒚-axis. In a graph showing inverse proportion, for any coordinate (𝒙, 𝒚) the product of 𝒙 and 𝒚 is always the same. (𝒙𝒚=12). 1 × 12 = 12, 2 × 6 = 12, 3 × 4 = 12, 4 × 3 = 12, 6 × 2 = 12, 12 × 1 = 12. As 𝒙 increases, 𝒚 decreases in the same proportion. The graph shows that 𝒙 and 𝒚 are inversely proportional.
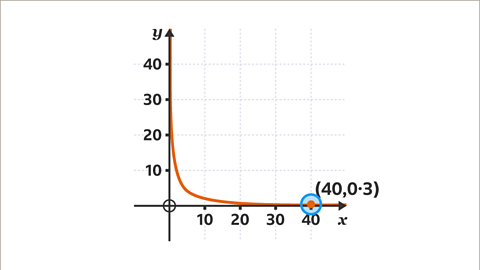
Image caption,
In a graph showing inverse proportion, the curve does not cross either axis. The point shown is (40, 0∙3) and it is plotted above the 𝒙-axis. In some graphs, the marked point may look like it crosses the axis, but the plotted point is above it.
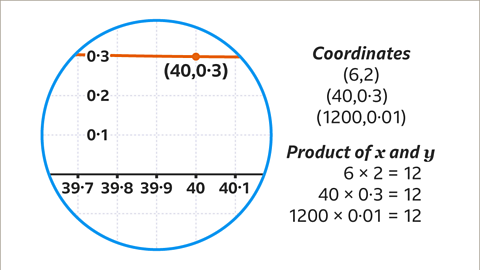
Image caption,
Here, the graph has been enlarged. The point (40, 0∙3) is above the 𝒙-axis. The curve is getting closer to the axis but will never touch it. For 𝒙 = 120, the coordinates will be (1200, 0∙01). The product of 𝒙 and 𝒚 is still 12. The equation of this graph can be given as 𝒚 = 12⁄𝒙 and also as 𝒙𝒚 = 12

Question

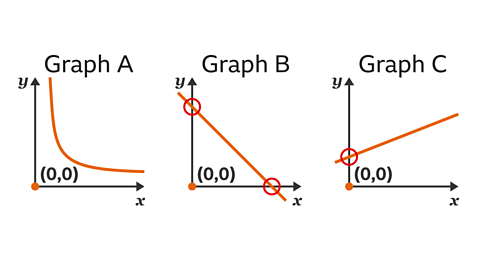
Explain why none of these graphs shows direct proportion.

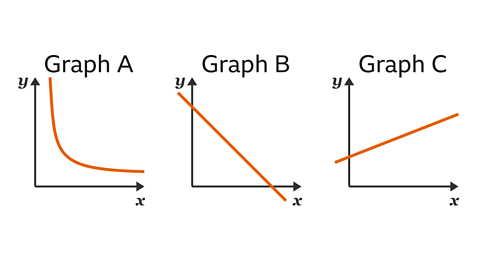
A diagram of three graphs labelled A to C. Graph A: Showing an inverse curve going down from to top of the y axis line to the end of the x axis line. Graph B: Showing a straight diagonal line going down from the top of the y axis line to the end of the x axis line. Graph C: Showing a straight diagonal line going up from a low point on the y axis line past the end of the x axis line.

How to draw a direct proportion graph using real-life data

To draw a graph for direct proportion:

Identify the ratio between the variables \((x:y)\).
Draw a table of values. Use the ratio to complete the table.
- The first coordinate is always (0, 0).
- One coordinate repeats the given ratio.
- Multiply to find at least one other coordinate.
- Three coordinates are needed, although more may be plotted.
Plot the coordinates.
Draw a straight line through the points and through the origin (0, 0).

Examples

Skip image gallery

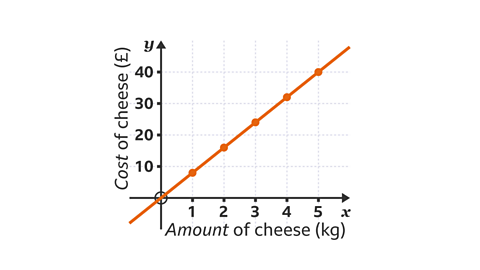
Image caption,
1 kg of cheese costs £8. Draw a graph of the amount of cheese (𝒙) against the cost (𝒚). Draw the graph to show the cost of up to 5 kg of cheese.
Image caption,
The cost of the cheese is directly proportional to the amount of cheese. The ratio of amount of cheese to cost is always 1 : 8. Draw a table of values. 0 kg of cheese will cost £0. 1 kg of cheese costs £8. Each kilogram of cheese costs £8 so multiply the amount of cheese in kg by 8 to find the cost. Each pair of values is a coordinate to be plotted.
Image caption,
The greatest amount of cheese is 5 kg. The 𝒙-axis (horizontal axis) should go up to 5. The greatest cost is £40. The 𝒚-axis (vertical axis) should go up to 40.
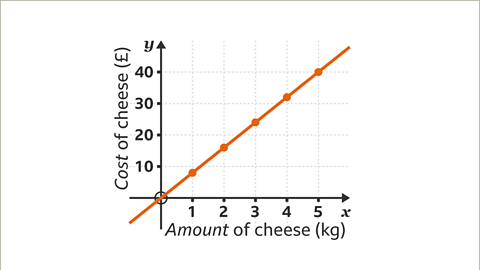
Image caption,
The points are plotted. The points are all in a straight line. A direct proportion graph can be drawn, using fewer points.
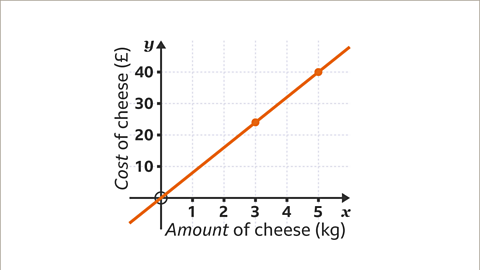
Image caption,
A direct proportion graph produces a straight line. Any two points will give a straight line. Three points are used to ensure the line is correct. Coordinates that are spread out help to give an accurate line. The graph can now be used to read the costs of other amounts of cheese.
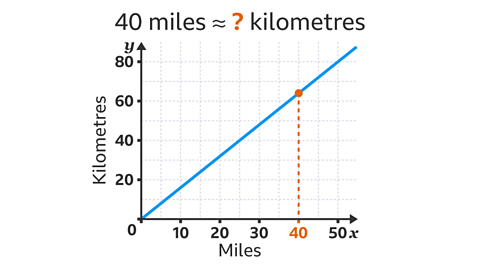
Image caption,
Given that 5 miles are approximately 8 kilometres, draw a graph of distance in miles (𝒙) against distance in kilometres (𝒚) to show the directly proportional relationship.
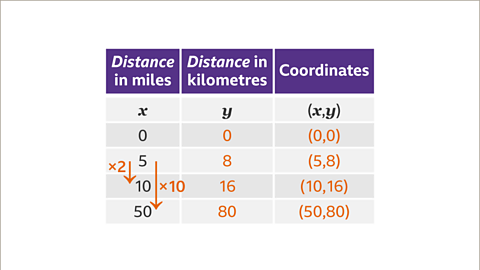
Image caption,
The distance in miles and the distance in kilometres are directly proportional. The ratio of miles : kilometres is always 5 : 8. A distance of zero in miles is zero in kilometres. This gives the point (0, 0). The given fact that 5 miles ≈ 8 kilometres gives the point (5, 8). These values can be multiplied to give other coordinates. For example, doubling the coordinate (5, 8) gives (10, 16). Multiplying the coordinate (5, 8) by ten gives (50, 80).
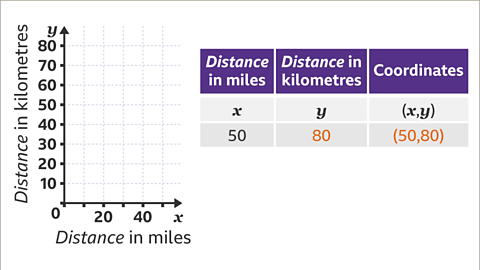
Image caption,
The greatest number of miles is 50 miles. The 𝒙-axis (horizontal axis) should go up to 50. The greatest number of kilometres is 80. The 𝒚-axis (vertical axis) should go up to 80
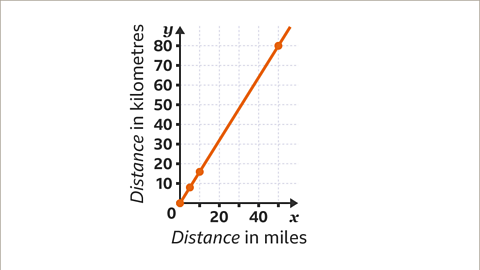
Image caption,
The points are plotted. The points are all in a straight line. Join the points to complete the graph. Values may be read from the graph when converting between miles and kilometres.

Question

One inch is approximately 2∙5 centimetres. Complete the table of values for the coordinates to be plotted.

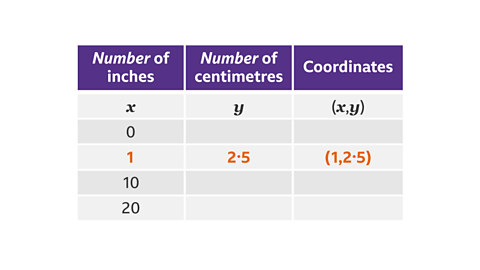
A diagram of a table. First column: Number of inches. X. Zero. One - highlighted. Ten. Twenty. Second column: Number of centimetres. Y. A blank box. Two point five – highlighted. A blank box. A blank box. Third column: Coordinates. X, y. A blank box. One, two point five – highlighted. A blank box. A blank box.

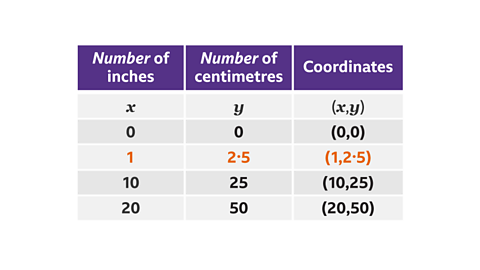
How to draw a graph for inverse proportion

To draw a graph for inverse proportion:

Identify the constant of the variables \((x)\).
Draw a table of values. Find of the product to complete the table.
- Each pair will have the same product.
- Several coordinates are needed because the graph is a curve.
Plot the coordinates.
Draw a smooth curve through the points.

Example

Skip image gallery

Image caption,
A rectangle has a fixed area of 24 cm². Draw the graph of the length of the rectangle (𝒙) against its width (𝒚).
Image caption,
The area of the rectangle is 24 cm². The product of the length and the width is always 24. List the factor pairs of the product (24) to generate the coordinates. Each factor pair will be used twice.
Image caption,
Draw a table of values. Use the factor pairs of the product (24) to generate the coordinates. Several coordinates are needed because the graph is a curve.
Image caption,
The largest factor of 24 is 24. The 𝒙- and 𝒚-axes go up to 24
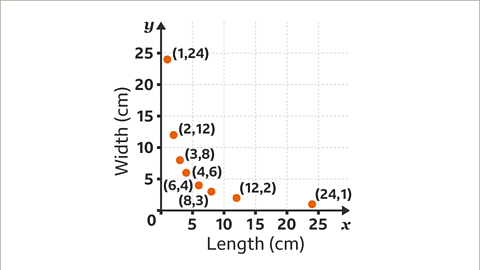
Image caption,
Plot the coordinates.
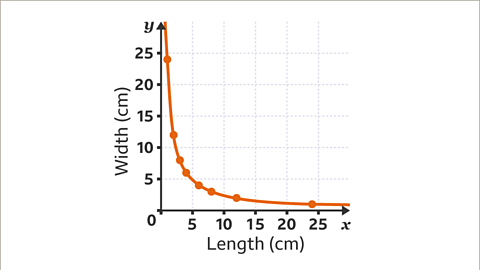
Image caption,
Draw a smooth curve through the plotted points.

Question

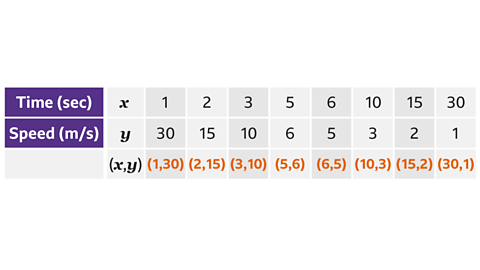
An object travels 30 metres. Complete the table of values for the coordinates (time and speed) to be plotted.

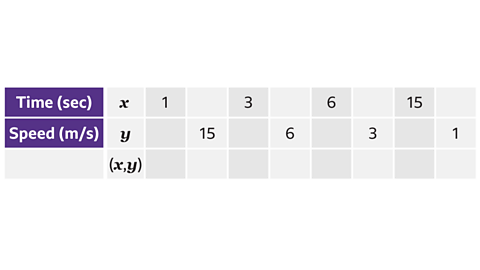
A diagram of a table with three rows. First row: Time open bracket sec close brackets. X. One. A blank box. Three. A blank box. Six. A blank box. Fifteen. A blank box Second row: Speed open brackets metres per second close brackets. Y. A blank box. Fifteen. A blank box. Six. A blank box. Three. A blank box. One. Third row – all values are in brackets: A blank box. X, y. The next eight boxes are blank.

Practise drawing direct and inverse proportion graphs

Practise drawing direct and inverse proportion graphs in this quiz. You may need a pen and paper to complete these questions.

Quiz

More on Direct and inverse proportion

Find out more by working through a topic

Conversion graphs
count
4 of 4
Direct proportion
count
1 of 4
Inverse proportion
count
2 of 4