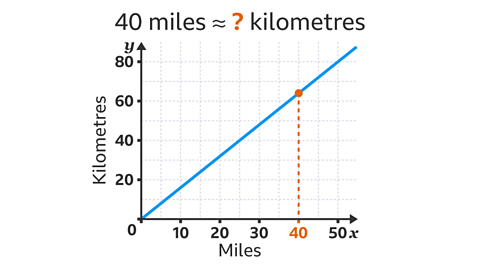
Key points
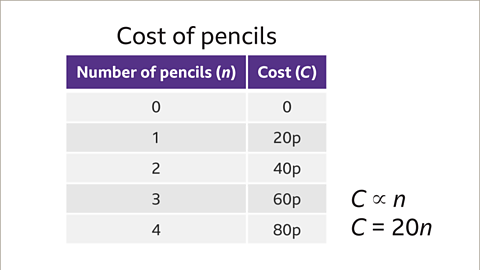
When two variables are direct proportionAs one variable increases the other variable increases at the same rate and when one is zero the other is also zero. For example the amount of cattle feed and its cost are directly proportional., as one increases the other also increases at the same rate (proportionally). So if one doubles, the other also doubles.
Direct proportion is written using the proportional symbol (∝)Used to signify that one variable is proportional to another. For example the number of chocolate bars (b) is directly proportional to their cost (C) can be written as b ∝ C . (∝). For example, if two variableA quantity that can take on a range of values. \(x\) and \(y\) are directly proportional to each other, then this statement can be represented as \(x\) ∝ \(y\).
When the proportionality sign (∝) is replaced with an equal sign (=), the equation is \(x = k y\). The constant value (often written as \(k\)) is known as the constant of proportionality and relates to the amounts that increase or decrease at the same rate.
To understand direct proportion, a good understanding of multiplication and division can be helpful. This is often referred to as multiplicative reasoningWorking flexibly with the concepts, strategies and representations of multiplication (and division) as they occur in a wide range of contexts. .

What is direct proportion?
To decide whether two variableA quantity that can take on a range of values. are direct proportionAs one variable increases the other variable increases at the same rate and when one is zero the other is also zero. For example the amount of cattle feed and its cost are directly proportional., check for the following:
- both variables have a value of zero at the same time
- as one variable increases/decreases, the other variable increases/decreases in the same proportion
Examples
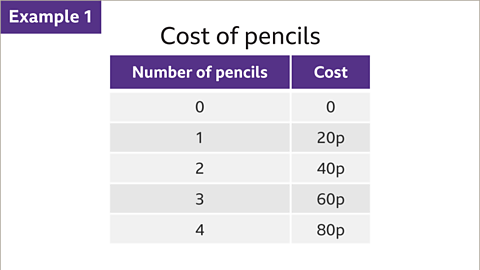
Image caption, The table shows the cost of buying a number of pencils. The more pencils bought, the greater the cost. The cost increases as the number of pencils increases. If no pencils are bought, there is no cost.
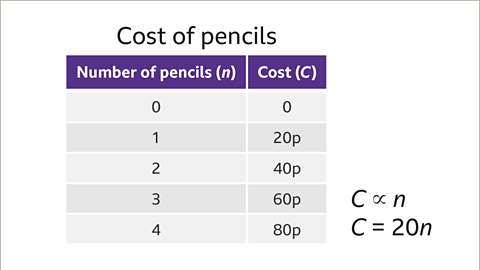
Image caption, The cost of the pencils (C) is directly proportional to the number of pencils (n). This can be written as C ∝ n. The constant of proportionality is 20, so C = 20n. For example, if n = 3, C = 20 × 3 If C = 20 × 3, the cost is 60p.

Image caption, Currency can be exchanged between pounds sterling (£) and euros (€).

Image caption, If two variables are directly proportional, both have a value of zero at the same time. This is true for the amounts of money in pounds and euros. The amounts of money in pounds and euros are directly proportional. £0 is the same as €0

Image caption, Two variables are directly proportional when as one variable increases/decreases, the other variable increases/decreases at the same rate. When £100 is doubled to £200, the amount of euros is also doubled (€120 × 2 = €240). The currencies are directly proportional. (Note: This is an example, exchange rates are variable).
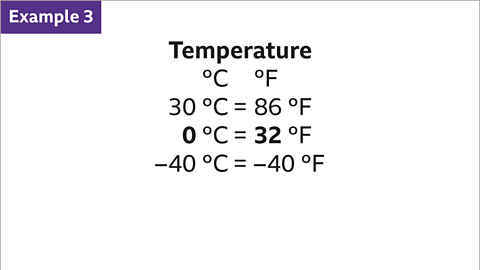
Image caption, Temperatures may be measured in degrees Celsius (°C) or degrees Fahrenheit (°F).
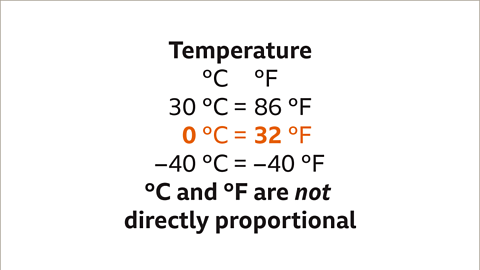
Image caption, If two variables are directly proportional, both have a value of zero at the same time. This is not true for temperature. 0°C is 32°F. Degrees Celsius and degrees Fahrenheit are not directly proportional.
1 of 7
Question
Are these different scone mixes directly proportional?
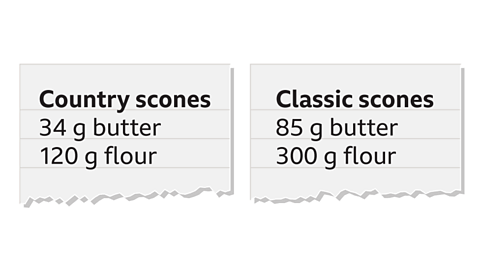
Two variables are directly proportional when as one variable increases/decreases, the other variable increases/decreases at the same rate.
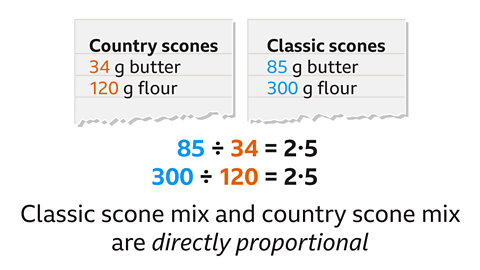
- Compare the amounts of butter in the two mixes: 85 ÷ 34 = 2∙5
The classic scone mix uses 2∙5 times the amount of butter of the country scone mix.
- Compare the amounts of flour in the two mixes: 300 ÷ 120 = 2∙5
The classic scone mix uses 2∙5 times the amount of flour of the country scone mix.
The classic scone mix uses 2∙5 times the amount of both butter and flour of the country scone mix, so the two scone mixes are directly proportional.
Direct proportion and multiplicative reasoning
multiplicative reasoningWorking flexibly with the concepts, strategies and representations of multiplication (and division) as they occur in a wide range of contexts. involves using multiplication and division to find other values.
Method:
Look for multiplicative links. Find a multiplication relationship (number of times greater) or division relationship (number of times smaller).
Repeat the same multiplication or division on the other variable.
Examples

Image caption, 5 ice creams cost £4.20 Find the cost of 10 ice creams.

Image caption, The number of ice creams is directly proportional to how much they cost. 5 ice creams cost £4.20 10 is 5 doubled. If the number of ice creams is multiplied by 2 (5 × 2 = 10), then the cost will also be doubled (£4.20 × 2).

Image caption, £4.20 × 2 = £8.40 The cost of 10 ice creams is £8.40

Image caption, The distance in miles and the distance in kilometres are directly proportional. Find the missing distances in the table.
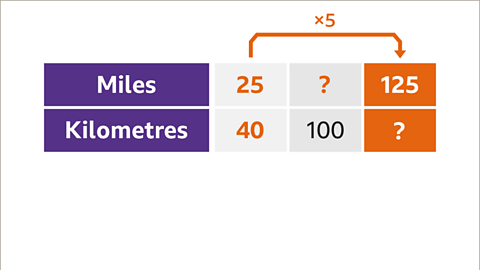
Image caption, Starting with the known fact (25 miles are the same as 40 km) look for multiplicative links. 25 × 5 = 125
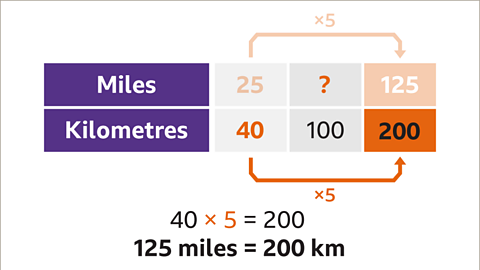
Image caption, If 25 miles × 5 = 125 miles, then 40 km × 5 will give the number of kilometres. 40 km x 5 = 200 km. This means 125 miles are 200 kilometres.

Image caption, 125 miles is 200 km. Look for multiplicative links. Divide 200 by 2 to get 100
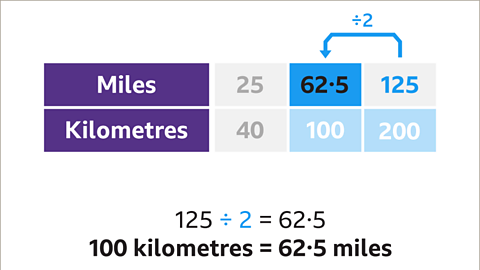
Image caption, To find how many miles are the same as 100 km, divide by 2 (125 ÷ 2 = 62∙5). 100 kilometres is 62∙5 miles.
1 of 8
Question
30 pies are sold for £45. How much do 5 pies cost?
The number of pies and the cost of the pies are directly proportional.
To find out how much 5 pies cost, work out how many times 5 goes into 30:
30 ÷ 5 = 6
The number of pies has been divided by 6. The cost now also needs to be divided by 6:
The cost of 5 pies is 45 ÷ 6
45 ÷ 6 = 7∙5
The cost of 5 pies is £7.50

Game - Direct proportion
Try out these direct proportion puzzles from our Divided Islands game.
Play the full Divided Islands game.
Direct proportion problems
Direct proportion problems can be solved by using the unitary method (finding one):
Find the value of one by dividing the total value by the quantity given.
Multiply the value of one by the number required.
Examples

Image caption, Five ice creams cost £4.20. Find the cost of seven ice creams.

Image caption, The number of ice creams is directly proportional to their cost. The unitary method means finding the cost of one ice cream. To do this, divide the total cost (£4.20) by the quantity given (5). 4∙2 ÷ 5 = 0∙84. One ice cream costs £0.84 (84p).

Image caption, The cost of seven ice creams is the cost of one ice cream multiplied by 7. 0∙84 × 7 = 5∙88. The cost of seven ice creams is £5.88

Image caption, Distances measured in kilometres and miles are directly proportional. Find the missing values in the table.
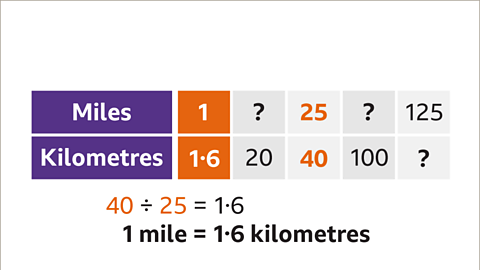
Image caption, 40 km are equal to 25 miles. Divide the number of km (40) by the number of miles (25) to find the number of kilometres equal to one mile. One mile is 1∙6 km. This fact can be used to find all the other values.

Image caption, One mile is 1∙6 km. The number of miles multiplied by 1∙6 will give the number of kilometres. 125 x 1∙6 = 200. This means 125 miles are 200 kilometres.

Image caption, One mile is 1∙6 km. The number of kilometres divided by 1∙6 will give the number of miles. 20 kilometres are 12∙5 miles. 100 kilometres are 62∙5 miles.
1 of 7
Question
30 pies are sold for £45. How much do 8 pies cost?
The number of pies and the cost of the pies are directly proportional.
The cost of one pie is the value of all the items (45) divided by the number of items (30):
45 ÷ 30 = 1∙50. The cost of 1 pie is £1.50
To find the cost of 8 pies, multiply the cost of one pie (£1.50) by 8:
1∙50 × 8 = 12
The cost of 8 pies is £12

Practise ratio and direct proportion
Practise ratio and direct proportion with this quiz. You may need a pen and a piece of paper to help you work things out.
Quiz
Real-world maths

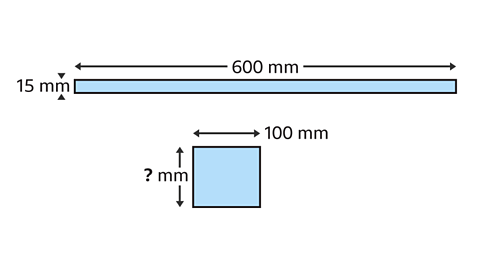
In planning the cost of fuel for a journey, direct proportion is used. If a car has an average fuel consumption of 40 miles per gallon, a journey of 600 miles would be expected to use 15 gallons (600 ÷ 40 =15)
Currency exchange is another example of direct proportion being used in real life. The quantity of pounds sterling (£) is directly proportional to the quantity of euros (€). The two currencies increase and decrease in the same ratio. When the quantity of pounds is doubled, so is the quantity of euros. When the quantity of pounds is zero, the quantity of euros is also zero. If the exchange rate between pounds and euros is £1 = 1.19€, then £2000 would give 2380€

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Direct and inverse proportion
Find out more by working through a topic
- count2 of 4
- count4 of 4