Trial and improvement - BBC Bitesize

Key points

and is a way of solving a problem by using a series of . For example, estimating what the length of a square is when you only know the area (cm²).
Guess what the answer might be then look at the outcome. Refine your guess (based on the size of your previous answer) until you get closer to the correct answer.
Careful consideration of your previous attempts will be more successful than a series of random guesses.
The most effective strategies use a approach. This involves narrowing down estimates to between 2 values before introducing decimals.

Using trial and improvement

There are steps which can be followed when using trial and improvement:

The first trial should be a whole number to make the calculation simpler.
- If the trial produces an answer which is too small, try a larger whole number with the second guess.
- If the trial produces an answer which is too big, try a smaller whole number with the next guess.
Continue trialling whole numbers until identifying that the answer lies between two consecutive integers.
The final guess should be halfway between the two integers that were identified.

Examples

Skip image gallery

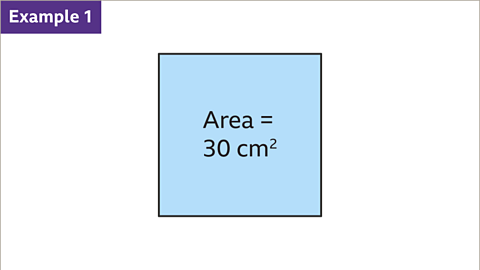
Image caption,
The first trial should be a whole number. Try using the length of 5 cm. 5 x 5 = 25. This is too small.
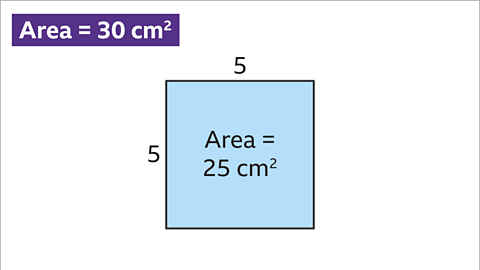
Image caption,
Try using the length of 6 cm. 6 x 6 = 36. This is too big. The length must be between 5 cm and 6 cm.
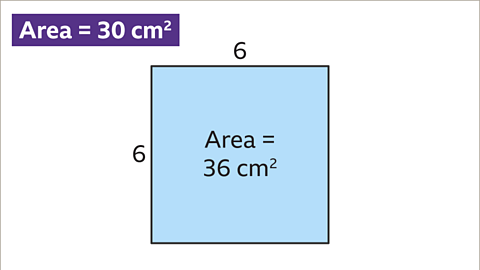
Image caption,
Try using the length of 6 cm. 6 x 6 = 36. This is too big. The length must be between 5 cm and 6 cm.
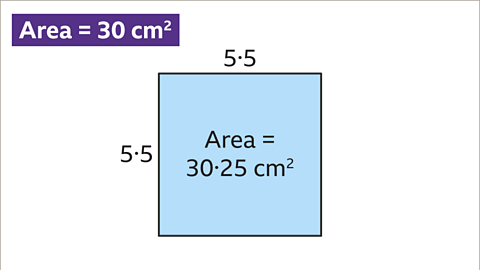
Image caption,
Try using the length of 5∙5 cm. 5.5 x 5.5 = 30∙25. This is too big.
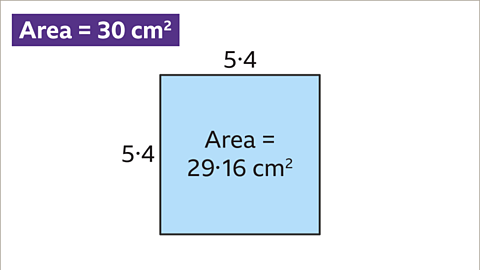
Image caption,
Try using the length of 5∙4 cm. 5∙4 x 5∙4 = 29∙16. This is too small.
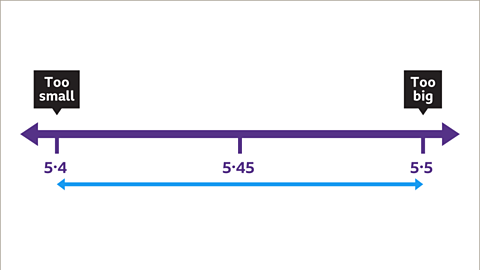
Image caption,
The answer lies between 5∙4 and 5∙5. Try the value halfway between them. For this example, this is 5∙45
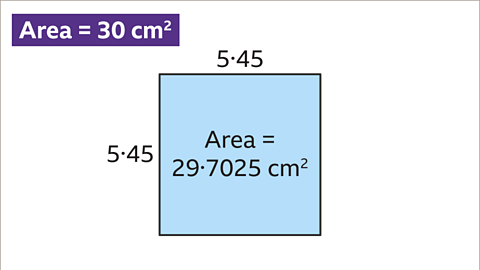
Image caption,
Try using the length of 5∙45 cm. 5∙45 x 5∙45 = 29∙7025. This is too small.
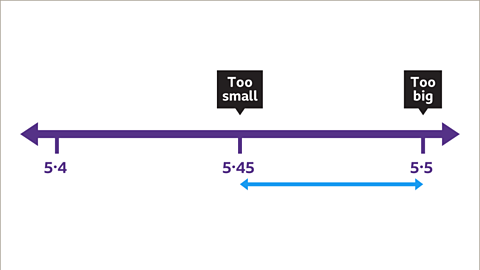
Image caption,
5∙45 cm was too small, meaning the answer lies between 5∙45 and 5∙5. Therefore, the answer must be closer to 5∙5 than 5∙4. The length of one side of the square is 5∙5 cm correct to 1 decimal place.
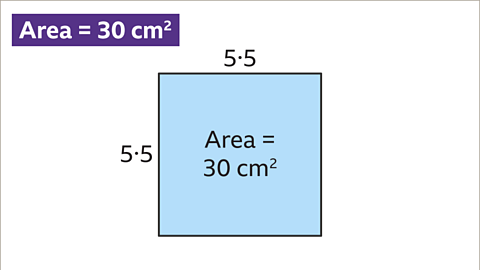
Image caption,
The area of a square is 30 cm², the length of one side of the square is 5∙5 cm correct to 1 decimal place.

Question

Which two numbers are the best initial trials to use when trying to find out the square root of 20?

Four sets of number options labelled A to D. Option A: Two and three. Option B: Four and five. Option C: Four and six. Option D: Five and six.

How to find more accurate answers

On most occasions finding the answer correct to 1 decimal place is acceptable. However, there are occasions where the answer needs to be found to a more accurate level. For example, to 2 decimal places.

Examples

How to find more accurate answers

Skip image gallery

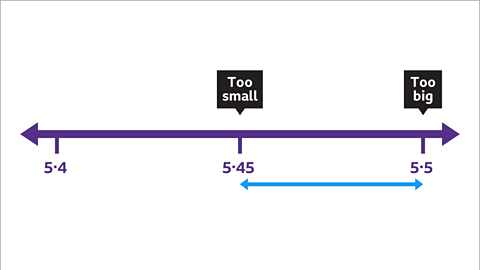
Image caption,
In the previous example, it was found that the answer lies between 5∙45 and 5∙5 (or 5.50) The next set of trials should contain 2 decimal places and lie between 5∙45 and 5∙50
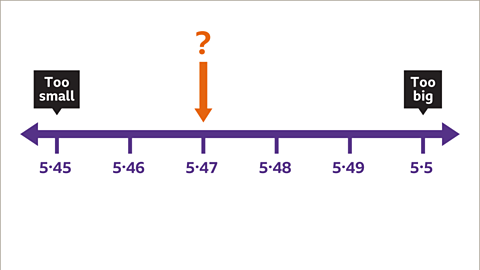
Image caption,
Pick a value between 5∙45 and 5∙50. Try using the length of 5∙47 cm. 5∙47 x 5∙47 = 29∙9209. This is too small.
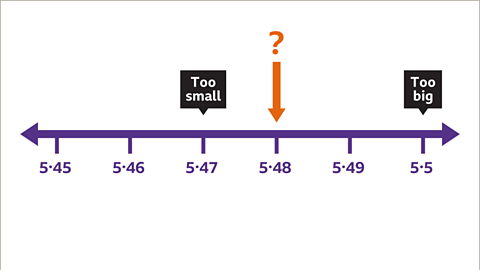
Image caption,
Try using the length of 5∙48 cm. 5∙48 x 5∙48 = 30∙0304. This is too big.
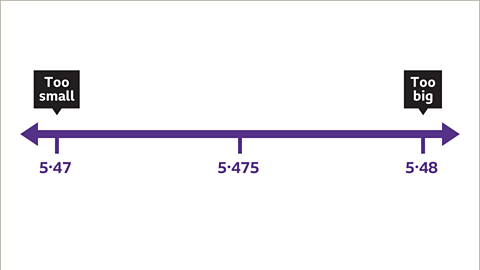
Image caption,
The answer lies between 5∙47 and 5∙48. Now try the value which is halfway between them (5∙475).
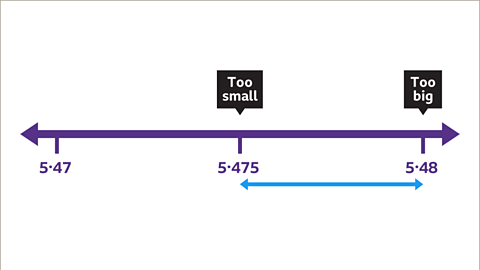
Image caption,
Try using the length of 5∙475 cm. 5∙475 x 5∙475 = 29∙975625. This is too small, meaning the answer lies between 5∙475 and 5∙48. Therefore, the answer must be closer to 5∙48 than 5∙47. The length of one side of the square is 5∙48 cm correct to 2 decimal places.
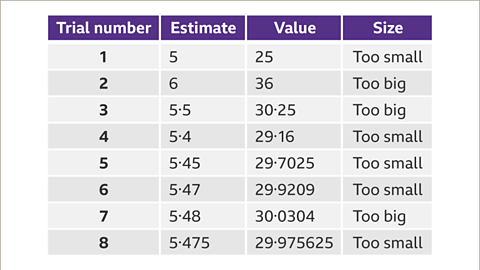
Image caption,
Recording your trials in a table is a good way to make sure you are being systematic, and not using the same number twice.
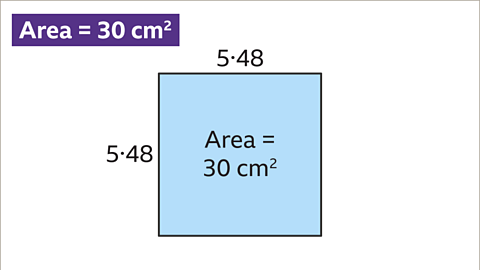
Image caption,
The area of a square is 30 cm², the length of one side of the square 5.48 cm correct to 2 decimal places.

Question

Looking at the estimates in the table, which number would be a sensible next trial?

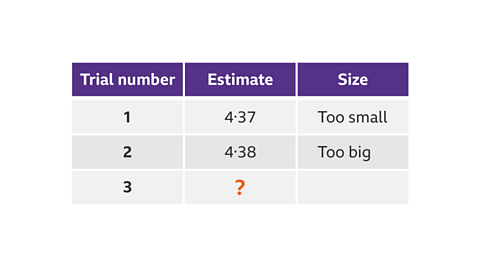
A table with three labelled columns and three rows of information. First column: Trial number. Second column: Estimate. Third column: Size. First row: One. Four point three seven. Too small. Second row: Two. Four three eight. Too big. Third row: Three. Orange question mark. A blank box.

Trial and improvement quiz

Practise trial and improvement in this activity.

Quiz

Real-world maths

A woman buying shoes online with shopping app on smart phone. — Image caption,
Buying items from an online auction where the customer and seller make an offer and counteroffer until they reach an agreed value.

Using trial and improvement is a strategy that is used in everyday life to help solve problems.

Haggling about the cost of an item when buying second-hand clothes on an app is like trial and improvement. The customer and seller take it in turns to make an offer and counteroffer until they reach a value that both feel is acceptable.

For example, a pair of shoes are priced at £20. The buyer offers the seller £15, and the seller responds with a counteroffer of £18. The buyer offers £16.50 and the seller makes a counteroffer of £17. The buyer accepts.