Calculating averages from grouped data - KS3 Maths

Key points

An image of a grouped frequency table. — Image caption,
Grouped frequency tables are a way of showing data in groups.

A grouped frequency table is a way of presenting data in groups called . Calculating the mean from a grouped frequency table uses a similar method to calculating the from an ungrouped frequency table.
The of each group is used as an value because the exact values of each piece of data cannot be seen. A new column is created for the midpoints of each group multiplied by the . This column is totalled, and divided by the total frequency to find an estimate for the mean.
The is the group in a frequency table that has the highest frequency.
The class that contains the value, is the group that contains the middle value. If there are \(n\) values, the middle value is the \( \frac{𝒏+1}{2} \)th value.
To find the modal class, identify the class with the highest frequency.

How to find averages in grouped frequency tables

To calculate an estimate for the mean from a grouped frequency table:

Set up a new column to write the midpoint of each class.
Set up another column to multiply each midpoint by its frequency.
Find the sum of the multiplications. This finds the estimated total of all the values in the frequency table.
Add the frequencies to find how many values there are.
Divide the total of all the values by how many values there are.

To find the class that contains the median, identify the class that contains the middle value. For a set of data with \(n\) values, the middle value is the \( \frac{𝒏+1}{2} \)th value.
To find the modal class, identify the class with the highest frequency.

Examples

Skip image gallery

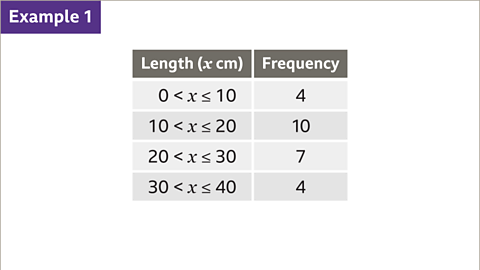
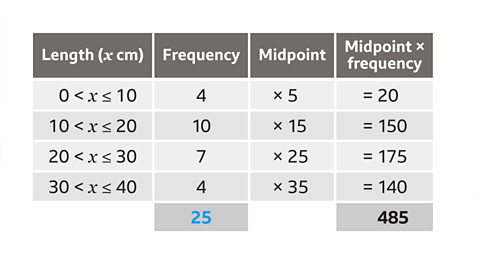
Image caption,
The table shows the lengths of 25 fish. Calculate an estimate for the mean length.
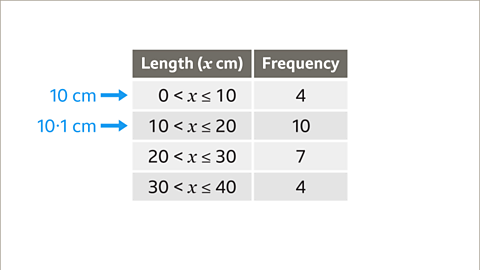
Image caption,
The 25 lengths have been grouped into four classes. The class 0 < 𝒙 ≤ 10 contains all the fish that are bigger than 0 cm, but smaller or equal to 10 cm. A length of 10 cm would be recorded in the first class, but a length of 10·1 cm would be recorded in the second class.
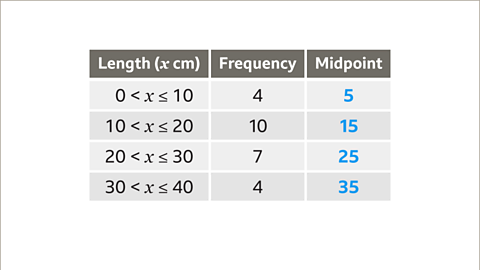
Image caption,
The data is grouped, so it is impossible to know the exact lengths. The exact mean cannot be calculated, so an estimate for the mean is calculated instead. Assume each length is in the middle of its group. For example, assume the 4 fish between 0 and 10 cm are 5 cm. The middle of each group is called the midpoint and is written in a new column.
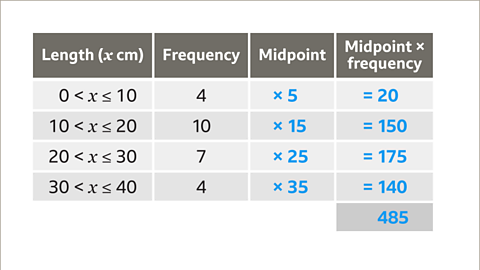
Image caption,
There are 4 fish estimated to be 5 cm each. The total estimated length of these fish is 4 x 5 = 20 cm. There are 10 fish estimated to be 15 cm each. The total estimated length of these fish is 10 x 15 = 150 cm. Make another new column to write in the results of all the multiplications. Add the figures in this column to calculate an estimate for the total length of all the fish. This would be 20 + 150 + 175 + 140 = 485 cm.
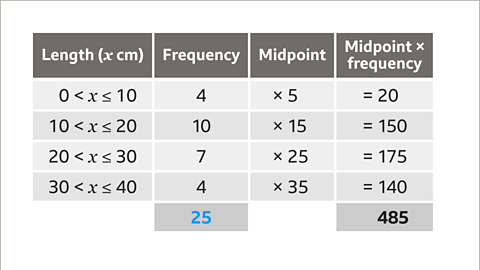
Image caption,
Add all the frequencies to find the total number of fish. This may also be given in the question. There are 25 fish.
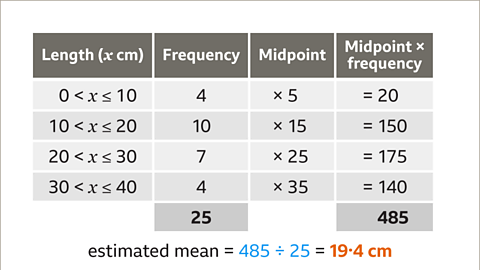
Image caption,
To calculate the estimate for the mean, divide the estimated total length of all the fish (485 cm) by how many fish there are (25). The estimate for the mean length is 485 ÷ 25 = 19·4 cm.
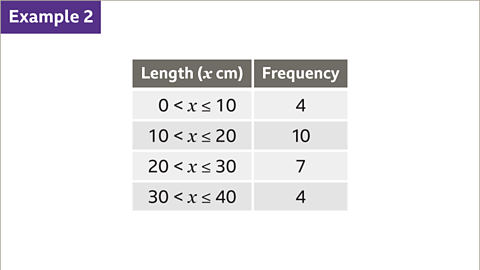
Image caption,
Work out the class that contains the median length of the 25 fish.
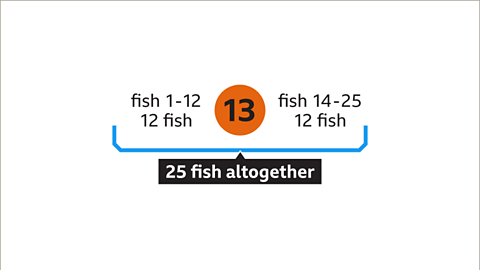
Image caption,
The median length is the length of the middle fish if they were placed in order from shortest to longest. There are 25 fish altogether. To find which fish would be in the middle, add 1 to the total, then divide by 2. The middle fish is the 13th fish. In general, if there are 𝒏 values altogether, the middle value is the ⁿ⁺¹⁄₂ th value.
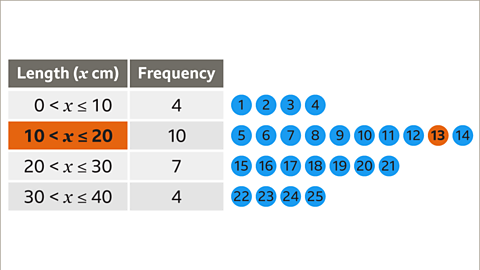
Image caption,
To find the class that contains the median length, find which group the 13th fish is in. There are 4 fish up to 10 cm long. There are another 10 fish between 10 and 20 cm long. This makes 14 fish between 0 and 20 cm long. The 13th fish must be between 10 and 20 cm long. The class that contains the median length is 10 < 𝒙 ≤ 20
Image caption,
The modal class is the group that contains the most fish. Find the group that has the highest frequency. The highest frequency is 10, so the modal class is 10 < 𝒙 ≤ 20

Question

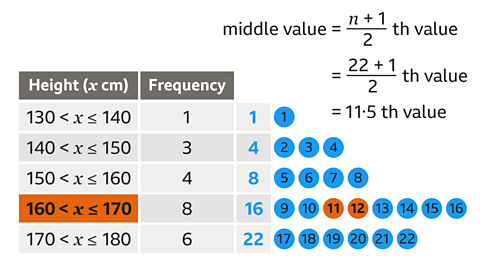
Which class contains the median height?

An image of a grouped frequency table. The table has two columns and six rows. The first column is labelled, height, x, measured in centimetres, and is populated with the groups, one hundred and thirty is less than x, is less than or equal to one hundred and forty. One hundred and forty is less than x, is less than or equal to one hundred and fifty. One hundred and fifty is less than x, is less than or equal to one hundred and sixty. One hundred and sixty is less than x, is less than or equal to one hundred and seventy. One hundred and seventy is less than x, is less than or equal to one hundred and eighty. The second column is labelled frequency and is populated with the numbers, one, three, four, eight, and six. The cells for the labels are coloured dark grey.

Practise working out averages from grouped data

Practise working out averages from grouped data with this quiz. You may need a pen and paper to help you with your answers.

Quiz

Real-life maths

An image of a scientist working at a computer. Test tubes and flasks are in the foreground. — Image caption,
A scientist will group data when looking at information and conducting research.

Grouped data is used in medical studies to identify if a treatment is more effective for certain groups of patients. Data could be grouped by age, amount of medicine given, or time since infection.

Calculating such as the mean, median or mode helps to summarise the data so that healthcare researchers can recommend specific treatments for patients.