KS3

Properties of 3D Shapes

Part ofMathsShapes

Key points

A series of seven images. Each image is a cube. The first three images have different faces of the cube coloured orange. In the first image the top and base faces are shaded. In the second image the left side and right side faces are shaded. In the third image the front and back faces are shaded. Written right, in orange: six faces. The fourth image has each corner, or vertex marked with a green dot. Written right, in green: eight vertices. The final three images have different edges of the cube highlighted pink. The first image has the four edges around the top face highlighted. The second image has the four vertical edges highlighted. The third image has the four edges around the base face highlighted. Written right, in pink: twelve edges. — Image caption,
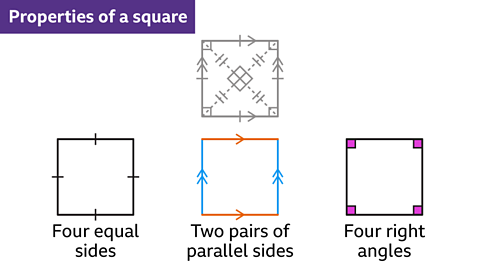
A cube has six faces, eight vertices and twelve edges.

A is a closed 2D shape with straight edges. The two dimensions are length and width.
A (plural ‘polyhedra’) is a fully enclosed 3D shape with faces that are all polygons. The three dimensions are length, width, and height. Polyhedra include , , and the .
The properties of a polyhedron are given by its , , and . The number of edges of a polyhedron is two less than the sum of the number of vertices and faces. This is given by the formula \(E\) = \(V\) + \(F\) – 2
3D shapes that are non-polyhedral include , and . These 3D shapes have at least one curved surface and at least one face that is not a polygon.

A series of seven images. Each image is a cube. The first three images have different faces of the cube coloured orange. In the first image the top and base faces are shaded. In the second image the left side and right side faces are shaded. In the third image the front and back faces are shaded. Written right, in orange: six faces. The fourth image has each corner, or vertex marked with a green dot. Written right, in green: eight vertices. The final three images have different edges of the cube highlighted pink. The first image has the four edges around the top face highlighted. The second image has the four vertical edges highlighted. The third image has the four edges around the base face highlighted. Written right, in pink: twelve edges. — Image caption,
A cube has six faces, eight vertices and twelve edges.

Understanding 3D shapes

A 3D shape with all straight edges and flat faces is a polyhedron. Other 3D shapes with least one curved surface are not polyhedra.

The platonic solids are regular polyhedra:
All the faces are regular polygons.
All the faces are .
The same number of faces meet at each vertex.
Other polyhedra include:
- , which are 3D polyhedra with six rectangular faces
- prisms, which are 3D shapes with a constant cross-section
- pyramids, which are 3D shapes with a polygonal base connected to an
3D shapes that are not polyhedra include:
- cylinders
- cones
- spheres

Examples

Skip image gallery

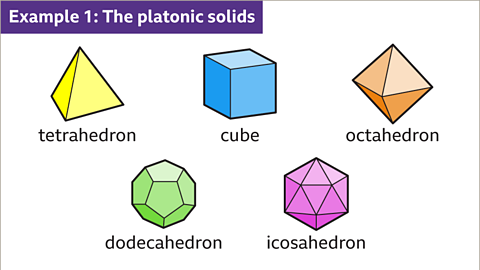
Image caption,
A 3D shape with regular polygonal faces, meeting at equal angles, is a platonic solid. There are five platonic solids, the tetrahedron, cube, octahedron, dodecahedron and icosahedron.
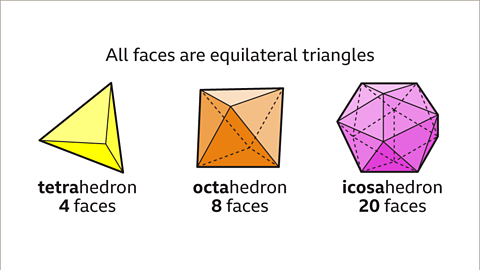
Image caption,
The tetrahedron, octahedron and icosahedron have faces that are all equilateral triangles. Tetra means four. A tetrahedron has four faces, with three triangles meeting at each vertex. Octa means eight. An octahedron has eight faces with four triangles meeting at each vertex. Icosa means twenty. An icosahedron has 20 faces with five triangles meeting at each vertex.
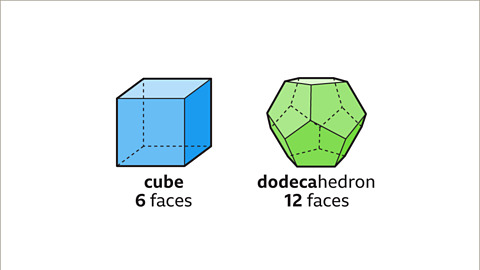
Image caption,
A cube has six square faces, with three squares meeting at each vertex. A dodecahedron has 12 pentagonal faces, with three pentagons meeting at each vertex.
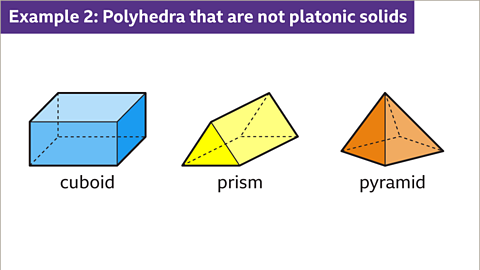
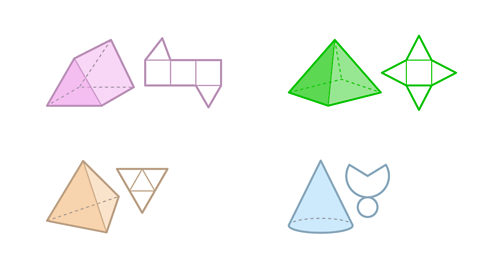
Image caption,
Other 3D shapes with flat polygon faces, straight edges and sharp vertices include cuboids, prisms and pyramids.
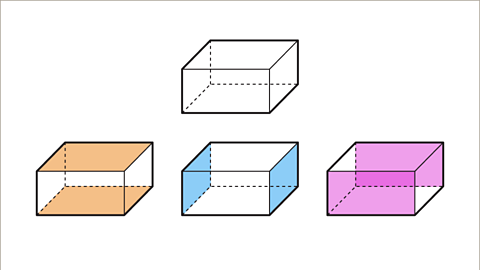
Image caption,
A cuboid has six rectangular faces. The opposite faces are congruent.
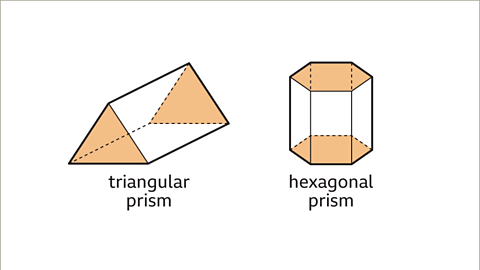
Image caption,
A prism is a 3D shape with a constant polygon shaped cross-section. A prism is named by the shape of its polygon cross-section. When the cross-section is a triangle, the prism is called a triangular prism. When the cross-section is a hexagon, the prism is called a hexagonal prism.
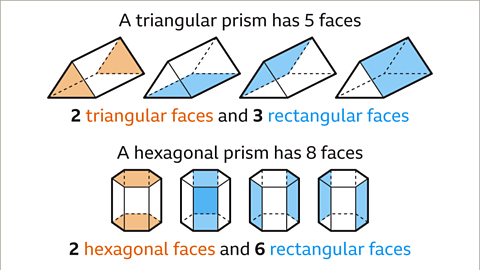
Image caption,
The faces of a prism are the congruent polygon ‘ends’, plus the rectangles that join them. The number of rectangular faces is equal to the number of sides of the polygon cross-section. A triangle has three sides. A triangular prism has three rectangular faces and two triangular faces, that is a total of five faces. A hexagon has six sides. A hexagonal prism has six rectangular faces and two hexagonal faces, that is a total of eight faces.
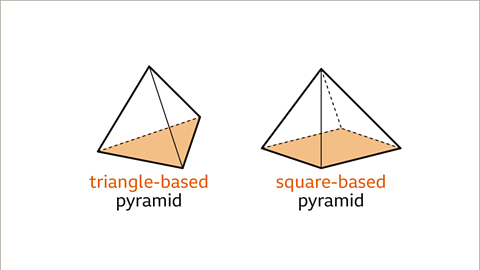
Image caption,
A pyramid is made up of a polygonal base face and triangular faces that meet at a point called the apex. A pyramid is named by the shape of its ‘base’. A pyramid with a triangular base is a triangle-based pyramid. A tetrahedron is a triangular pyramid with all equilateral triangle faces. A pyramid with a square base is a square-based pyramid.
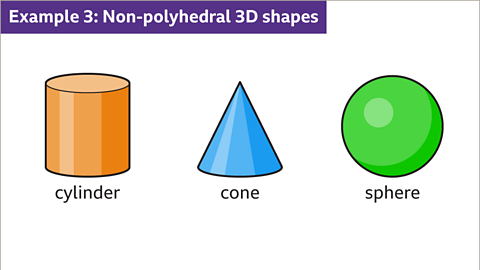
Image caption,
3D shapes that are non-polyhedral include cylinders, cones, and spheres. At least one face is not a polygon. At least one face has a curved surface. A cylinder has a constant circular cross-section, two circular faces and one curved rectangular face. A cone has a circular base and one curved face made from a sector of a circle. A sphere is completely curved, a ball shape.
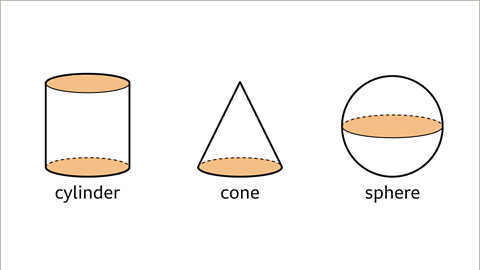
Image caption,
A cylinder has a constant circular cross-section, two circular faces and one curved rectangular face. A cone has a circular base and one curved face made from a sector of a circle. A sphere is completely curved, a ball shape.

Question

Name this 3D shape.

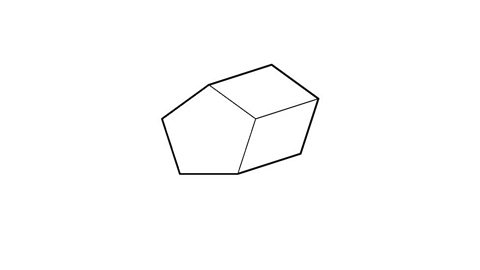
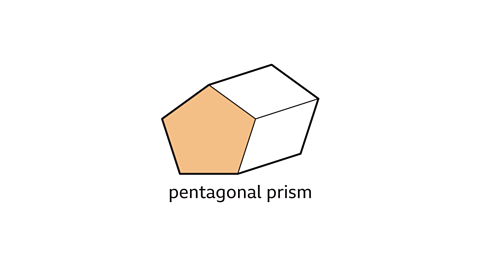
An image of a three dimensional shape. The shape has a regular cross section throughout its length. The cross section is a polygon with five sides.

Understanding vertices, edges and faces of polyhedra

Polyhedra are described by counting:
For all polyhedra the number of edges is two less than the sum of the number of vertices and faces. This is shown in the formula \(E\) = \(V\) + \(F\) – 2

Examples

Skip image gallery

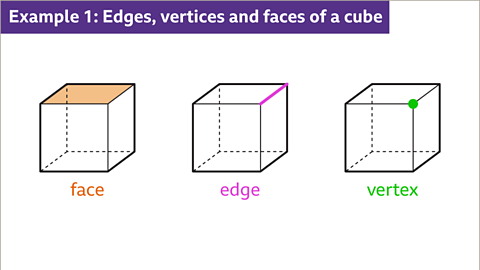
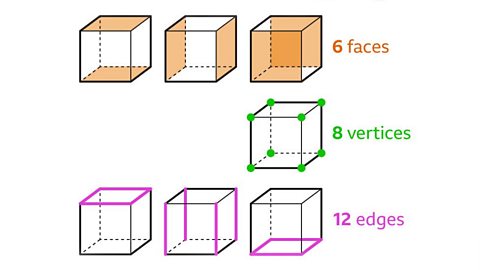
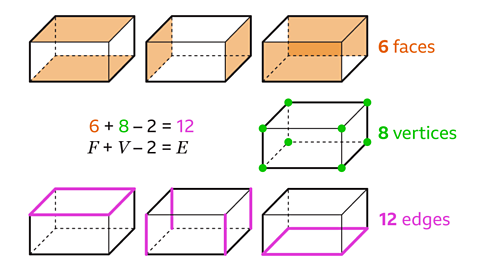
Image caption,
The flat surface of a cube is a face. Each face of a cube is a square. Two faces are joined by an edge. Three square faces meet at a vertex.
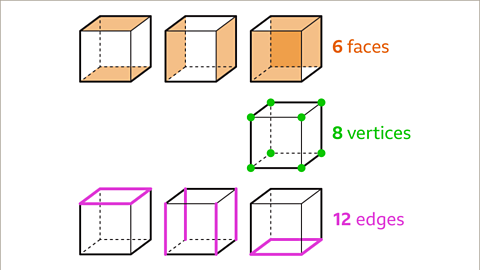
Image caption,
A cube has six faces, eight vertices and twelve edges.
Image caption,
For any 3D shape that is a polyhedron, the number of edges is equal to two less than the sum of the vertices and faces. This is the formula 𝑬 = 𝑭 + 𝑽 – 2
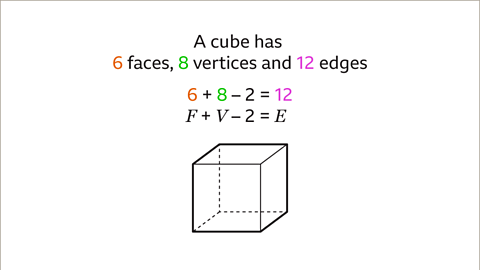
Image caption,
For a cube, 𝑬 = 12, 𝑭 = 6 and 𝑽 = 8. The number of edges can be calculated by adding the number of faces and vertices and subtracting two. 𝑭 + 𝑽 – 2 = 𝑬. 6 + 8 – 2 = 12
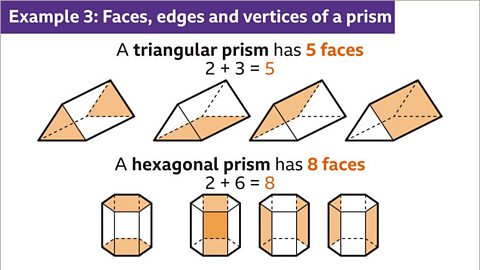
Image caption,
A prism has two end faces that match the cross-section, plus a rectangular face for each side of the end face. A triangle has three sides. A triangular prism has five faces, the two triangles for each end plus three rectangular faces that join them. A hexagonal prism has eight faces, the two hexagons for each end plus six rectangular faces that join them.
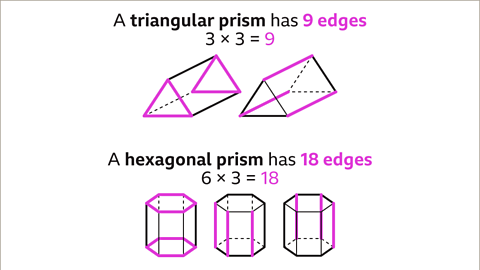
Image caption,
The number of edges of a prism is the number of edges of an end face, multiplied by three. A triangular prism has three edges for each end face and a further three for the edges joining them together. 3 × 3 = 9. A triangular prism has nine edges. A hexagonal prism has six edges for each end face plus a further six for the edges that join them. 6 × 3 = 18. A hexagonal prism has 18 edges.
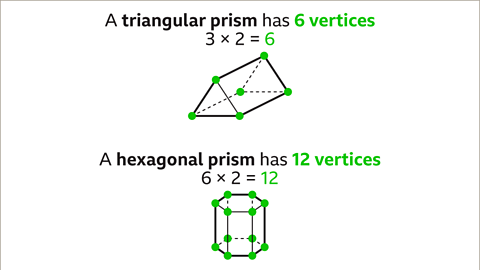
Image caption,
The vertices of a prism are at each end of the 3D shape. The number of vertices is twice the number of vertices of an end face. A triangular prism has two triangular faces. 3 × 2 = 6. A triangular prism has six vertices. A hexagonal prism has two hexagonal end faces. 6 × 2 = 12. A hexagonal prism has 12 vertices.
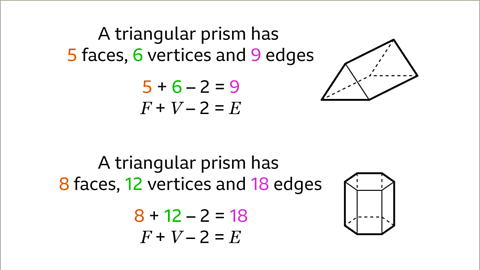
Image caption,
The formula 𝑬 = 𝑭 + 𝑽 – 2 works for prisms because they are a type of polyhedron. For a triangular prism, 𝑭 = 5, 𝑽 = 6 and 𝑬 = 9. 5 + 6 – 2 = 9. 𝑭 + 𝑽 – 2 = 𝑬. For a hexagonal prism, 𝑭 = 8, 𝑽 = 12 and 𝑬 = 18. 8 + 12 – 2 = 18. 𝑭 + 𝑽 – 2 = 𝑬
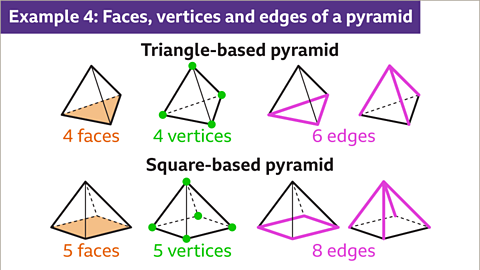
Image caption,
A pyramid has one more face than the number of sides of its base. A triangle-based pyramid has four faces. A square-based pyramid has five faces. The vertices of a pyramid are around the polygon base plus the apex vertex. A triangle-based pyramid has four vertices. A square-based pyramid has five vertices. The number of edges of a pyramid is twice the number of edges of the base. A triangle-based pyramid has six edges, 3 × 2 = 6. A square-based pyramid has eight edges, 4 × 2 = 8
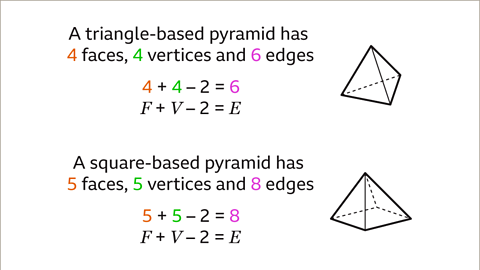
Image caption,
The formula 𝑬 = 𝑭 + 𝑽 – 2 works for pyramids because they are a type of polyhedron. For a triangle-based pyramid 𝑭 = 4, 𝑽 = 4 and 𝑬 = 6. 4 + 4 – 2 = 6. For a square-based pyramid 𝑭 = 5, 𝑽 = 5 and 𝑬 = 8. 5 + 5 – 2 = 8. 𝑭 + 𝑽 – 2 = 𝑬.

Questions

Show that the formula \(E\) = \(V\) + \(F\) – 2 is true for a cuboid.

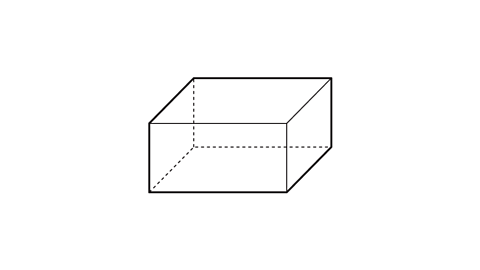
An image of a cuboid.

Practise working out properties of 3D shapes

Practise working out properties of 3D shapes with this quiz. You may need a pen and paper to help you with your answers.

Quiz

Real-life maths

An image of different shaped dice. Each dice is a platonic solid. — Image caption,
All the faces of a platonic solid are congruent.

are used to make dice.

One property of a platonic solid is that all its faces are the same (congruent). The chance of landing on each of the congruent faces is equally likely, meaning the dice are fair.

6-sided cube dice are most common. Other types of dice are often used in role-playing games.

An image of different shaped dice. Each dice is a platonic solid. — Image caption,
All the faces of a platonic solid are congruent.

More on Shapes

Find out more by working through a topic

3D shapes and nets
count
4 of 4
Properties of triangles
count
1 of 4
Properties of quadrilaterals
count
2 of 4