1 - 1 + 1 - 1 +... », l'explication curieuse d'un mathématicien sur la façon dont Dieu a créé le monde
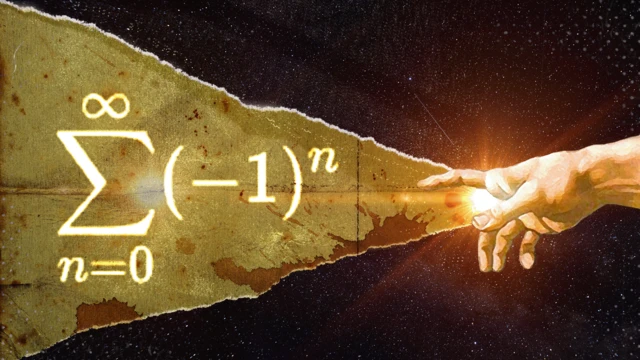
Crédit photo, Caroline Souza/BBC
Les mathématiques pourraient-elles expliquer le sens de la vie, de l'univers et de tout le reste ?
Je n'en sais rien. Mais cela vaut toujours la peine d'essayer.
L'une des tentatives de démonstration de la probabilité d'une chose aussi déconcertante que le début de tout a été faite avec quelque chose qui est représenté comme vous le voyez dans l'image ci-dessus.
Avec ∑, ∞ et plusieurs n, cela peut paraître un peu intimidant.
Ce sont des opérations simples, mais si on les répète à l'infini, elles deviennent une somme qui a occupé les plus grands mathématiciens depuis le XVIIIe siècle.
La grande question était : quel est le résultat de cette somme infinie ?
Une réponse intuitivement évidente est qu'il n'y a pas de réponse : si elle se poursuit à l'infini, elle variera entre 0 et 1 sans jamais atteindre une seule valeur.
Cependant, il ne s'agit là que de l'une des quatre options envisagées au fil du temps.
Et la plus surprenante est peut-être celle qui a le plus convaincu le premier mathématicien à avoir attiré l'attention sur cette énigme, connue sous le nom de série de Grandi.
Luigi Guido Grandi (1671 - 1742) est un prêtre, philosophe, mathématicien et ingénieur né à Crémone, aujourd'hui en Italie.
Son intérêt pour les mathématiques a été lent à se manifester, mais son premier livre, Geometrica divinatio Vivianeorum problematum, publié en 1699, lui a valu d'être reconnu dans son pays et à l'étranger.

Crédit photo, AnonMoos
Des informations vérifiées à portée de main
Cliquez ici et abonnez-vous !
Fin de Promotion WhatsApp
Sa réputation l'amènera à devenir, en 1707, le mathématicien de la cour du grand-duc de Toscane, Cosme III de Médicis, et à ce titre, il sera responsable d'importants projets d'ingénierie, dont le drainage de la vallée de la Chianna.
Il collabore également à la publication de la première édition des œuvres de Galilée (1718), publie une version italienne des Éléments d'Euclide (1731), conseille le pape Clément sur la réforme du calendrier et introduit en Italie les idées de Gottfried Leibniz sur le calcul.
Également admiré à l'étranger, il devient membre de la prestigieuse Royal Society de Londres en 1709, après qu'Isaac Newton a publié ses travaux sur la théorie de la musique.
L'un de ses travaux les plus admirés est son étude de la rose polaire, une famille de courbes qui ressemblent à des fleurs, qu'il appelle rhodoneas (du grec rhodon, rose), dans son livre Flores Geometrici (1725).
Mais c'est une autre de ses œuvres qui a suscité non seulement l'intérêt de ses pairs, mais aussi une vive polémique autour de la série qui porte son nom.
0, 1, 1/2
Le livre, publié en 1703 et intitulé Quadrature du cercle et de l'hyperbole, contient un résultat qui a attiré beaucoup d'attention.
Grandi a étudié la somme infinie de 1 - 1 + 1 - 1 + - - -
et a observé que l'ajout de parenthèses donnait des résultats différents.
(1 - 1) + (1 - 1) + (1 - 1)... donne 0 + 0 + 0..., qui est égal à 0.
Mais si on l'écrivait ainsi : 1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 1)... alors la somme serait 1 + 0 + 0 + 0..., ce qui donnerait 1.
En soi, c'est surprenant.
Plus surprenante encore est son affirmation selon laquelle la somme d'une infinité de 0 est égale à 1/2.

Grandi a préféré expliquer ce résultat par une parabole dans laquelle il imagine deux frères qui héritent de leurs parents un bijou de grande valeur
Il leur est interdit de le vendre et le diviser en deux en détruirait la valeur.
Les frères se sont mis d'accord pour alterner la propriété du bijou, en l'échangeant chaque jour de l'an.
En supposant que l'accord se poursuive indéfiniment, la propriété du bijou peut être représentée, du point de vue de chaque frère, par la série suivante
1 - 1 + 1 - 1 + - - -
Ainsi, chaque frère est propriétaire du bijou pendant la moitié du temps, de sorte que la valeur de cette série serait de 1/2.
Vous serez peut-être surpris, mais plusieurs mathématiciens éminents de l'époque étaient d'accord pour dire que c'était la réponse.
Le célèbre Leibniz est parvenu à la même conclusion par d'autres méthodes et a déclaré que 1/2 était la réponse qui lui semblait juste, bien qu'il ait reconnu que l'argument était plus « métaphysique que mathématique ».
Le Suisse Leonhard Euler, l'un des plus grands et des plus prolifiques mathématiciens de tous les temps, a fait ses propres calculs et a écrit en 1760 :
« Il ne fait aucun doute qu'en fait la série 1 - 1 + 1 - 1 + 1 - 1 + etc. et la fraction 1/2 sont des quantités équivalentes et qu'il est toujours permis de substituer l'une à l'autre sans erreur ».
Comme eux, d'autres mathématiciens à travers l'Europe ont discuté des séries infinies et sont parvenus à leurs propres conclusions.
Mais l'un d'entre eux, en particulier, n'aimait pas beaucoup les idées de Grandi.

Crédit photo, Getty Images
Alessandro Marchetti (1633 - 1714), professeur de mathématiques à l'université de Pise, n'appréciait guère la renommée internationale de Grandi.
Pour tenter de le discréditer, il critiqua sévèrement son livre.
En réponse, Grandi publie une deuxième édition de Quadratura... en 1710.
Mais cette fois, il est autorisé à inclure un commentaire que les censeurs avaient exigé de retirer de la version précédente, condition qu'il accepte, non sans réticence.
Cette déclaration est encore plus surprenante que les résultats qu'il a obtenus.
Sa réflexion était qu'en ajoutant des parenthèses à l'expression 1 - 1 + 1 - 1 + - - il était possible d'obtenir, de différentes manières, 1 ou 0, « donc l'idée de la création ex nihilo était parfaitement plausible ».
La création ex nihilo est une création à partir de rien.
De plus, si une quantité finie pouvait être obtenue à partir d'une somme de zéros infiniment étendue, il fallait « reconnaître cette puissance infinie », une force qui, même « en multipliant ce qui en soi n'est rien, le transforme en quelque chose, de la même manière que la division d'une grandeur finie la fait dégénérer en rien ».
Et c'est « par la puissance infinie du Dieu créateur que toutes les choses ont été faites à partir de rien, et que toutes les choses peuvent être réduites à rien ».
Ainsi, Grandi semblait être parvenu à une preuve mathématique que Dieu avait tout créé à partir de rien.
Marchetti publie alors une attaque contre cette deuxième édition en 1711, à laquelle Grandi répond par un autre article en 1712.
La controverse se poursuivit jusqu'à la mort de Marchetti en 1714.
L'intérêt pour la série de Grandi n'a cependant pas faibli.
Bien que ses arguments ne résistent pas à l'examen mathématique moderne, il existe un cadre pour les sommes infinies dans lequel la série de Grandi est égale à 1/2.
Ce cadre est connu sous le nom de somme de Cesàro, en l'honneur du mathématicien italien Ernesto Cesàro de la fin du 19e siècle.
Cependant, selon diverses sources, l'opinion générale des mathématiciens d'aujourd'hui est que la valeur de la série de Grandi n'est ni 1, ni 0, ni 1/2 : le résultat de cette somme infinie est nul.
Mais s'il y en avait un, ce serait 1/2.