Les bizarreries de Pi, le nombre qui a le plus d'adeptes au monde (et qui n'est même pas un nombre)
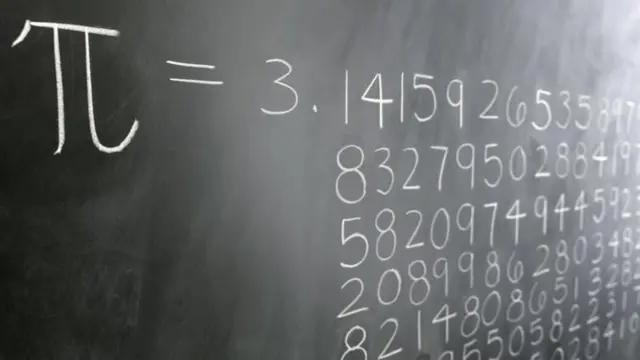
Crédit photo, Getty Images
- Author, Anabel Forte Deltell
- Role, The Conversation*
Quatorze mars : 14/3 ou 3/14 si on le lit dans la nomenclature anglaise. Lorsque nous disons "trois quatorze", nous pensons rapidement à un nombre qui nous rappelle le lycée.
Il est d'ailleurs fort possible qu'en l'entendant, nous suivions la chaîne : quinze, quatre-vingt-douze, soixante-cinq... pour autant que notre mémoire se souvienne des chiffres du nombre singulier Pi.
En 2009, le Congrès américain a officiellement déclaré ce jour, le 14 mars, comme étant le π Day.
Le succès a été immédiat et l'idée s'est répandue jusqu'à ce qu'en 2019, l'UNESCO en fasse la Journée internationale des mathématiques.
Depuis, de plus en plus de personnes se joignent à la célébration chaque année, avec π comme symbole de ceux d'entre nous qui aiment les mathématiques.
Traduit avec www.DeepL.com/Translator (version gratuite)
Pi n'est pas vraiment un nombre
Pi est la seizième lettre de l'alphabet grec (π) et, en mathématiques, nous l'utilisons pour représenter quelque chose de beaucoup plus intéressant qu'un nombre (je ne dis pas que les nombres ne le sont pas). La première bizarrerie de Pi est donc qu'il ne s'agit pas d'un nombre. Mais alors, si ce n'est pas un nombre, qu'est-ce que Pi ?
Pi représente le rapport entre la longueur de la circonférence et son diamètre. Une proportion qui a la particularité (ici sa deuxième bizarrerie) d'être constante, c'est-à-dire d'avoir toujours la même valeur quelle que soit la taille de la circonférence.
En particulier, dans la géométrie euclidienne - que l'on doit à Euclide (325-265 av. J.-C.) et qui nous assure qu'une seule droite passe par deux points - la valeur constante de Pi est si particulière (et cela fait trois fois) qu'elle est irrationnelle.
Ce n'est pas qu'elle ait perdu sa raison mais que, bien qu'elle résulte de la division du périmètre par le diamètre, elle ne peut jamais être exprimée comme la division de deux nombres entiers.
Si le diamètre d'une roue est une valeur "exacte", sans décimales, l'espace qu'elle couvrira en se retournant ne le sera pas. Mais alors, de combien sera-t-il ? Nous approchons d'une question clé, la valeur de Pi... mais passons d'abord à une autre de ses bizarreries, la quatrième déjà.

Crédit photo, Getty Images
Pi est transcendant. Ce n'est pas qu'il soit si important qu'il transcende (ce qu'il fait), mais qu'il est transcendant, sans n. Cette propriété mathématique nous assure que Pi ne sera jamais la solution d'un polynôme.
Un polynôme ? Vous vous souvenez certainement de ce terme lors de vos études de mathématiques. Les polynômes sont des équations dans lesquelles l'inconnue est élevée à un ou plusieurs nombres naturels, par exemple x2 + x + 3 = 0.
Eh bien, quels que soient les exposants et les nombres utilisés, il n'existe aucun polynôme pour lequel x vaut Pi. Il convient également de mentionner qu'il s'agit d'une propriété à laquelle de nombreux nombres ne satisfont pas. À ce stade, il a donc déjà été prouvé que Pi est bizarre, mais le meilleur reste à venir. Parlons maintenant de sa valeur.
L'insaisissable valeur de Pi
Comme nous l'avons dit au début, la valeur constante de Pi (dans la géométrie euclidienne) est 3,141592... mais, précisément parce qu'elle est irrationnelle, nous savons qu'elle aura une infinité de décimales. Infinies, comme on dit, sans fin et, pour aggraver les choses, dans ce cas, non seulement elles sont infinies, mais elles ne suivent aucun modèle.
Elles semblent être placées au hasard, tous les chiffres de 0 à 9 ayant la même probabilité d'apparaître. En fait, leurs valeurs peuvent être utilisées comme un générateur de nombres aléatoires et il est possible de rechercher parmi eux n'importe quelle succession de chiffres, même le numéro d'identification d'une personne au hasard, qui se trouve forcément quelque part.

Crédit photo, Getty Images
Des informations vérifiées à portée de main
Cliquez ici et abonnez-vous !
Fin de Promotion WhatsApp
Cependant, le plus important dans cette propriété de Pi est qu'elle est devenue une source d'inspiration pour le travail de tant de personnes.
Depuis les temps les plus reculés (il existe des preuves que Pi était connu des Babyloniens dès 2 000 ans avant J.-C.), des efforts ont été déployés pour établir sa valeur aussi précisément que possible. En particulier, l'un des premiers à porter ses fruits fut Archimède de Syracuse (287 - 212 av. J.-C.), qui mit au point une méthode pour délimiter la valeur de cette constante rare.
Archimède a utilisé des polygones inscrits (ceux qui se trouvent à l'intérieur de la circonférence) et circonscrits (ceux qui contiennent la circonférence à l'intérieur). De cette manière, la valeur du périmètre de la circonférence serait toujours comprise entre le périmètre du polygone inscrit et celui du polygone circonscrit.
En ajoutant de plus en plus de côtés aux polygones, Archimède est parvenu à donner une fourchette de valeurs pour Pi, dont l'erreur maximale est de 0,040 % par rapport à la valeur réelle... Allez, on y est presque, on y est presque, on y est presque.
L'idée d'Archimède a été suivie par beaucoup d'autres de nature très différente, certaines même du point de vue des probabilités et des statistiques, comme ce fut le cas de Georges-Luis Leclerc (1707-1788), le comte de Buffon.
En particulier, Leclerc a trouvé le nombre Pi en essayant de déterminer la probabilité qu'une aiguille lancée sur un ensemble de lignes parallèles tombe sur l'une des lignes droites. Après plusieurs calculs, il est parvenu à la conclusion que, si les lignes étaient séparées par la même distance que la longueur de l'aiguille, la probabilité était égale à 2 divisé par Pi.
De cette manière, il était facile d'approcher Pi en lançant de nombreuses aiguilles, en observant la proportion d'aiguilles qui coupaient effectivement les lignes parallèles et en la comparant à la probabilité exacte.
Cependant, avec l'avènement de l'ère informatique est apparue la cinquième bizarrerie de Pi, à savoir le fait qu'il s'agisse d'un nombre calculable. En particulier, Alan Turing a défini en 1936 qu'un nombre est calculable s'il existe un algorithme qui nous permet d'approximer sa valeur avec un nombre prédéterminé de décimales.
63 trillions de décimales de Pi ont été calculées
Partant de ce principe, une machine ENIAC a réussi en 1949 à battre le record humain et à calculer les 2037 premières décimales de Pi, donnant le coup d'envoi d'une course qui a atteint les 63 000 milliards de chiffres (européens) avec lesquels il a été calculé en 2021 par une équipe de la Haute école spécialisée du canton suisse des Grisons.
Mais Pi n'est pas seulement une entité mathématique curieuse qui a tiré les ficelles de la pensée humaine depuis l'antiquité. Pi est, comme l'assure Rhett Alain, un nombre étonnant qui apparaît naturellement là où l'on s'y attend le moins : dans l'estimation de notre position par GPS, dans le mouvement du pendule d'une horloge murale ou encore dans la manière dont un assistant vocal est capable de reconnaître que l'utilisateur veut, par exemple, se faire raconter une blague.
Mais Pi est surtout l'excuse parfaite pour célébrer les mathématiques et tout ce qu'elles nous apportent chaque quatorze mars. Bonne journée internationale des mathématiques !

* Anabel Forte Deltell est titulaire d’un doctorat en mathématiques et est chargée de cours à l’Université de Valence (Espagne), au sein du département de statistique et de recherche opérationnelle.
Cet article a été publié dans The Conversation et reproduit ici sous licence Creative Commons. Cliquez ici pour lire la version originale et voir les liens vers les études citées.