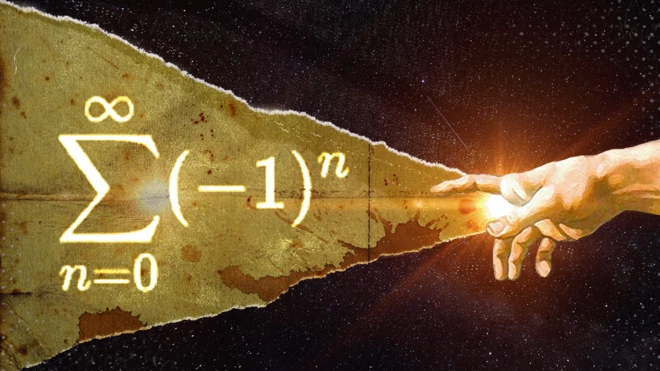Pourquoi les mathématiciens veulent mettre fin à l'infini (et ils n'aiment pas non plus les nombres énormes)

Il y a quelques jours, je suis tombé sur un article du magazine New Scientist intitulé "Pourquoi les mathématiciens veulent détruire l'infini... et ils pourraient le faire".

Je n'ai pas pu résister à l'envie de le lire car j'avoue que l'infini me fascine.

Pour moi, l'infini est la liberté créative, intellectuelle et émotionnelle.

Je suis également étonné que nous puissions concevoir un concept aussi étonnant dès le plus jeune âge : "Jusqu'à l'infini et au-delà!" , comme dit Buzz Lightyear de Toy Story.

Peut-être parce que nous le pressentons en regardant l'horizon, ou parce que nous le ressentons en découvrant notre capacité à aimer.

Donc l'idée que quelqu'un pourrait vouloir le détruire m'a alarmé, particulièrement s'il s'agissait de mathématiciens.

Et c'est que les mathématiques me fascinent aussi... de loin, car mes connaissances sont limitées, mais suffisantes pour rappeler que les mathématiciens de la Grèce antique observaient l'énigmatique infini avec attention.

De Zénon d'Élie (~450 avant J.C.), avec ses fameux paradoxes sur le concept et sa manifestation dans le mouvement et la continuité, jusqu'à Archimède (IIIe siècle avant J.-C.), qui a exploré l'infini et démontré comment additionner un nombre infini de sommes pour résoudre des problèmes géométriques, préfigurant le calcul infinitésimal.

Au 17ème siècle, Isaac Newton et Gottfried Wilhelm Leibniz ont développé et formalisé cette branche fondamentale des mathématiques qui se concentre sur l'étude du changement et du mouvement.

Je me souviens aussi de mon étonnement en comprenant ce que le mathématicien allemand de la fin du XIXe siècle Georg Cantor a démontré : qu'il n'y avait pas un seul infini mais plusieurs, et que certains étaient plus grands que d'autres.

Avec sa théorie des ensembles, Cantor a établi la première théorie mathématique qui a permis de gérer l'incommensurable.

Depuis lors, l'infini a été la pierre angulaire des mathématiques et de la physique contemporaines, et donc de notre monde, y compris le quotidien, car il joue un rôle essentiel dans notre technologie et science.

Alors, d'où vient le désir de l'éliminer?

"Parce que l'infini n'est qu'une illusion", m'a dit Doron Zeilberger, professeur distingué de l'université Rutgers dans le New Jersey, un mathématicien illustre et multi-primé.

Mais c'est aussi un dissident, un éminent ultrafinitiste, comme s'autonomme le groupe de mathématiciens, philosophes, informaticiens et physiciens qui pendant des décennies a été considéré comme radical mais qui, bien que restant une petite minorité, est écouté.

Ils remettent en question le concept de l'infini, et font valoir que même des nombres finis mais énormes, par exemple 10, pourraient être insignifiants.

Même si nous comptions chaque atome de l'univers observable, nous n'atteindrions jamais ce chiffre, alors quel sens y a-t-il à parler d'elle?

Cette illusion

"Dans ma philosophie, les mathématiques ont pris la mauvaise voie en embrassant l'infini," m'a dit Zeilberger.

"Les gens ne se rendaient pas compte parce que c'était comme une illusion d'optique", a-t-il ajouté, "comme l'ancienne croyance que la Terre était plate".

"Les gens ont cru que l'univers est infini, et certaines personnes le croient encore, mais d'autres pensent qu'il est fini. Il n'est pas limité, parce que vous pouvez toujours aller de l'avant, mais il est fini, comme notre planète", dit-elle.

Illimité mais pas infini ? Peut-être : en théorie on pourrait faire le tour du monde sans arrêt pour un temps indéfini, mais cela ne veut pas dire que la Terre est infinie.

"Donc je pense que c'est un univers mathématique

"En"Mais avec l'invention de ce concept artificiel d'infini, tout est devenu très complexe, élaboré et tordu.

"Je ne peux pas dire que les mathématiques classiques sont logiquement erronées, mais qu'elles sont inutilement compliquées.

Rétrospectivement, si vous aviez réalisé que le monde est fini, et il y a un nombre qui est le plus grand nombre possible, tout serait plus simple".

Mais s'il y a un nombre naturel maximum, qu'arrive-t-il à l'addition de 1, une des preuves de l'existence de l'infini?

Simplement, selon Zeilberger, dans une circularité très élégante, on revient à 0... ce qui dans notre exemple de faire le tour du monde indéfiniment, serait comme, à un moment donné, arriver au point de départ original.

"Ce que je propose est un peu analogue à la révolution d'Albert Einstein, qui a démontré que la vitesse de la lumière est la plus rapide : vous ne pouvez pas aller plus vite d'environ 300.000 kilomètres par heure.

"Einstein a eu de la chance : il est arrivé à un certain nombre. Je n'ai aucune idée de ce qui est le plus grand nombre, mais il est hors de propos, vous pouvez l'appeler de toute façon.

"Le fait est qu'avec lui vous pouvez recréer tous les mathématiques et les rendre beaucoup plus simples. Bien que j'avoue que le faire serait vraiment très fastidieux".

Le fait est que les ultrafinistes proposent une solution radicale : éliminer l'infini et se limiter aux nombres "faisables", pour décompliquer la science et la rendre plus pratique.

Mathématiciens rebelles

Qu'est-ce qui rend un nombre "réalisable"?

Pour Rohit Parikh, de la City University de New York, qui a développé l'une des premières théories ultrafinitistes formelles dans les années 1970 et introduit l'idée de "nombres réalisables", la clé est de maintenir un lien avec l'activité humaine.

"Il faut fixer une limite à un moment donné. Les choses doivent être reliées à l'activité humaine".

Si un nombre ne peut pas être nommé, calculé, stocké, transmis ou même identifié de manière cohérente sous des contraintes physiques, existe-t-il vraiment en tant qu'objet mathématique ?

Pensez par exemple au nombre de Skewes, un nombre qui apparaît dans la théorie des nombres, si extrêmement grand qu'il semble avoir plus de chiffres que ceux qui tiennent dans l'univers.

Bien qu'il soit absurdement élevé, il a été utile pour plusieurs raisons, y compris montrer jusqu'où les mathématiques peuvent aller dans la recherche de certitude, et démontrer que les résultats peuvent être certains, même si elles sont inutiles dans la pratique directe.

Cela provoquerait le rejet des ultrafinitistes : le nombre de Skewes et beaucoup d'autres beaucoup plus petits que lui seraient bien au-dessus de cette limite qui, insistent-ils, devrait être tracée.

Mais quelle est cette limite?

Il y a une anecdote qui est souvent citée et implique le père de l'ultrafinitisme moderne, Alexander Yessenin-Volpin, un mathématicien qui était un éminent activiste des droits humains en Union soviétique, pour lequel il a été emprisonné en 1968 a raconté Harvey Friedman dans "Problèmes philosophiques en logique".

En 2000, il a eu l'occasion de soumettre à Yessenin-Volpin l'objection de la plupart des mathématiciens à l'idée de fixer des limites.

"Il m'a demandé d'être plus spécifique. J'ai donc commencé par 21 et je lui ai demandé si c'était ''réel'' ou quelque chose comme ça. Presque immédiatement dit oui. J'ai ensuite demandé pour 2 2, et il a de nouveau dit oui, mais avec un retard perceptible. Puis 2 3, et oui, mais avec plus de retard.

« Cela s'est reproduit plusieurs fois, jusqu'à ce qu'il devienne évident comment il gérait cette objection. Bien sûr, il était prêt à répondre oui à chaque fois, mais il lui fallait 2¹⁰⁰ fois plus de temps pour répondre oui à 2¹⁰⁰ qu'à 2¹. Il n'y avait aucun moyen pour lui d'aller très loin avec cela. »

L'anecdote illustre l'idée fondamentale de l'ultrafinitisme : l'existence des nombres est de plus en plus remise en question au fur et à mesure qu'ils grandissent.

Question de foi

Dans cette vision, l'arithmétique correspond à ce qui peut être fait, limité par le temps, l'espace et les ressources.

Il y a une frontière au-delà de laquelle tout est futile.

Et cette frontière est en quelque sorte imposée par les ordinateurs, qui peuvent faire des calculs que ceux qui ont introduit l'infini et imaginé des nombres énormes ne pouvaient que rêver.

"Parfois, vous avez une équation différentielle si compliquée que personne ne sait exactement comment la résoudre", a déclaré Zeilberger.

"Mais en utilisant des ordinateurs, vous pouvez obtenir une très bonne approximation, assez bonne pour tous les buts pratiques, et c'est ainsi que cela se fait".

Une grande partie du travail moderne avec les mathématiques réside déjà dans le fini, de la cryptographie et de la vérification formelle aux structures de données et aux algorithmes aléatoires.

En physique aussi, il y a ceux qui essaient d'appliquer le finitisme dans l'espoir de trouver de meilleures théories pour décrire notre monde.

Pour le physicien américano-suédois Max Tegmark, l'infini est un beau concept, mais il ruine la physique.

"Nos meilleures simulations informatiques, qui décrivent avec précision tout - de la formation des galaxies au climat du futur et les masses des particules élémentaires- utilisent uniquement des ressources informatiques finies en traitant tout comme fini", a écrit dans son livre "Cette idée doit mourir".

Cependant, si nous relions étroitement les mathématiques et la physique à la capacité limitée des ordinateurs, ne courons-nous pas le risque de lier notre sagesse et l'aventure de l'exploration à ce qui est possible plutôt qu'à ce qui est possible?

Si l'on bannit à l'infini des mathématiques, l'imagination ne sera-t-elle pas limitée et la créativité restreinte?

"Je comprends que vous aimez l'infini et je ne vais pas vous dissuader : certains de mes meilleurs amis aiment l'infini", a plaisanté Zeilberger.

"Le point est que vous devez savoir qu'il y a un moyen de refaire tous les mathématiques, au moins ce qui est nécessaire pour la science et la technologie, par des moyens complètement finitistes".

A la fin, c'est presque comme une question de foi.

"L'infini peut exister ou non, Dieu peut exister ou non, mais il n'y a pas besoin de l'un des deux en mathématiques," il a ajouté.

Cliquez ici pour lire plus d'histoires de BBC News World.

Abonnez-vous ici à notre nouvelle newsletter pour recevoir chaque vendredi une sélection de nos meilleurs contenus de la semaine.

Vous pouvez également nous suivre sur YouTube, Instagram, TikTok, X, Facebook et notre chaîne WhatsApp.

N'oubliez pas que vous pouvez recevoir des notifications dans notre application. Téléchargez la dernière version et activez-les.