Mixed numbers, proper and improper fractions explained

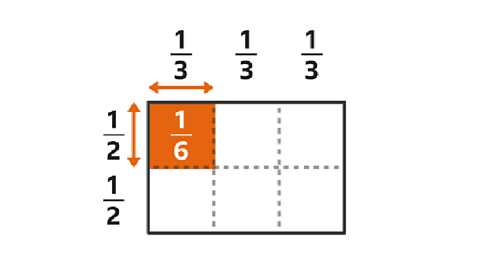
Key points

There are different types of fractions - a fraction can be , or a .

A proper fraction has a that is less than its .
An improper fraction has a numerator greater than its denominator. An improper fraction is always greater than one whole.
An improper fraction can also be written as a mixed number. This is an and a fraction next to each other.
Proper fractions, improper fractions and mixed numbers can be represented by a diagram or written in figures.
To process calculations, different types of fractions are used. Improper fractions are used when multiplying and dividing. Mixed numbers may be preferred for adding and subtracting.

What are mixed numbers, proper and improper fractions?

A fraction can be a proper fraction or an improper fraction. An improper fraction written as an integer with a fraction is called a mixed number.

A has a numerator that is less than the denominator. In a diagram a proper fraction is shown as less than a whole shape.
An has a numerator that is greater than the denominator. In a diagram an improper fraction is shown as greater than one whole shape.
A is an integer written with a fraction. In a diagram a mixed number is shown as a combination of complete shapes and parts of a shape.

Example: types of fractions

Skip image gallery

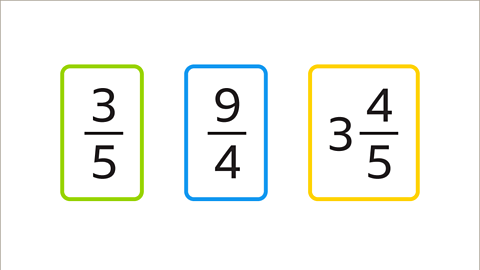
$3 fractions in different shaded boxes. Three fifths with a green outline. Nine quarters with a blue outline. Three and four fifths with a yellow outline.$
Image caption,
A fraction can be a proper fraction or an improper fraction. A value greater than one whole can be an improper fraction or a mixed number.
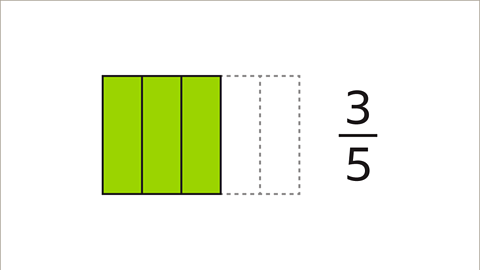
Image caption,
The numerator is less than the denominator. 3⁄5 is a proper fraction.
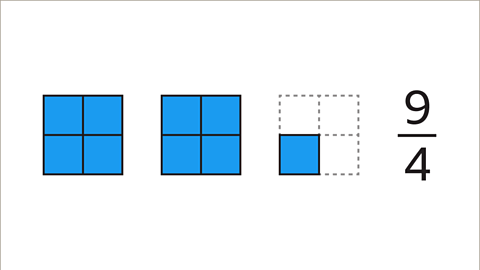
$3 squares split into four. Nine of the parts are shaded. The fraction shows nine quarters.$
Image caption,
The numerator is greater than the denominator. 9⁄4 is an improper fraction.
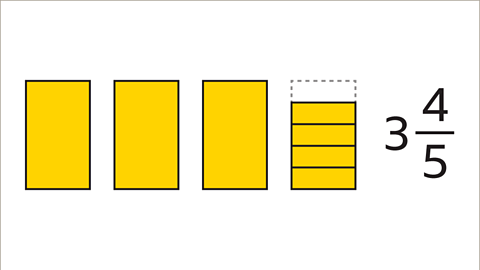
$4 rectangles. Three and shaded in yellow. The last has four of five parts shaded in yellow. The fraction is written next to it: three and four fifths.$
Image caption,
The number is written as an integer and a fraction. 3 4⁄5 is a mixed number.

How to convert a mixed number to an improper fraction

Multiply the by the denominator and add the numerator.
This gives the numerator of the improper fraction.
The denominator stays the same.

Example: convert 3 1⁄2 and 5 2⁄9 to improper fractions

Skip image gallery

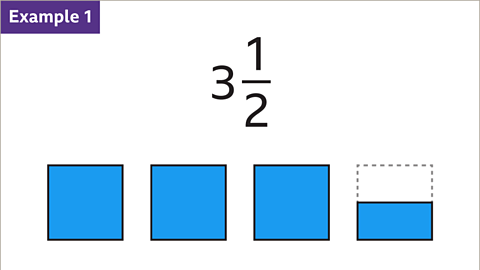
$Example 1. A diagram shows three and one half in blue. The fraction three and one half is written above.$
Image caption,
Convert 3 1⁄2 to an improper fraction.
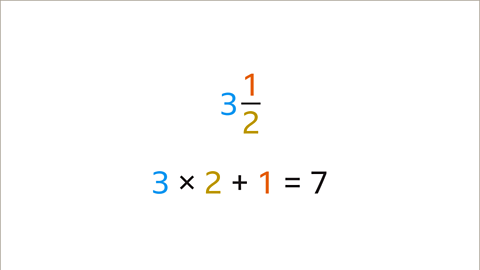
Image caption,
Multiply the integer (3) by the denominator (2) and add the numerator (1). This equals 7. The numerator of the improper fraction is 7
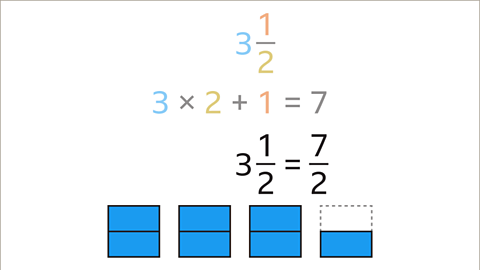
Image caption,
The denominator (2) does not change. 3 1⁄2 converts to 7⁄2 as an improper fraction.
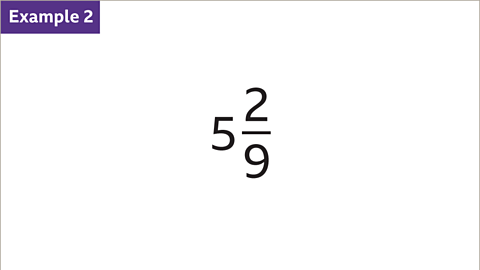
Image caption,
Convert 5 2⁄9 to an improper fraction.
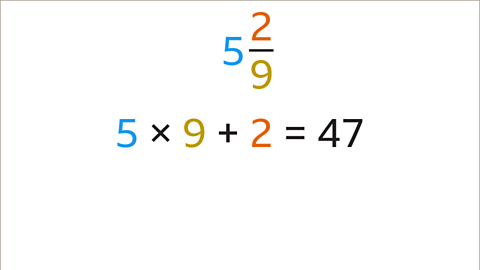
Image caption,
Multiply the integer (5) by the denominator (9) and add the numerator (2). This equals 47. The numerator of the improper fraction is 47
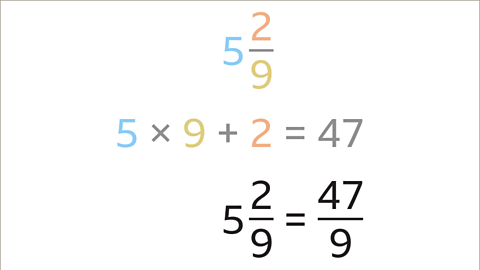
Image caption,
The denominator (9) does not change. 5 2⁄9 converts to 47⁄9 as an improper fraction.

Question

Convert $ 4 \frac{2}{3} $ to an improper fraction.

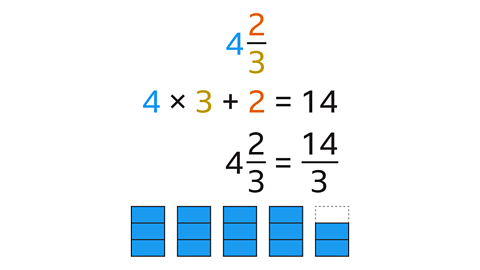
How to convert an improper fraction to a mixed number

Divide the by the .
The whole number is the part of the mixed number.
In a mixed number, the is the numerator of the fraction.
The denominator stays the same.

Example: convert 9⁄4 and 23⁄6 to mixed numbers

Skip image gallery

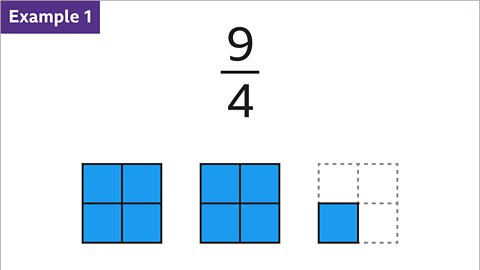
$Example 1. A diagram showing nine quarters shaded blue. The fraction nine quarters is above.$
Image caption,
Convert 9⁄4 to a mixed number.
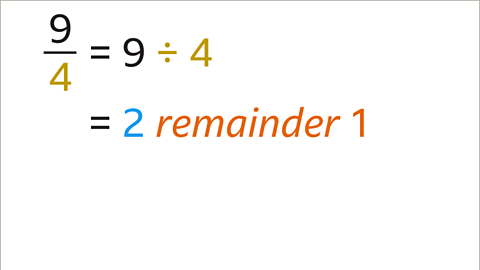
Image caption,
Divide the numerator (9) by the denominator (4). 9 ÷ 4 = 2 remainder 1
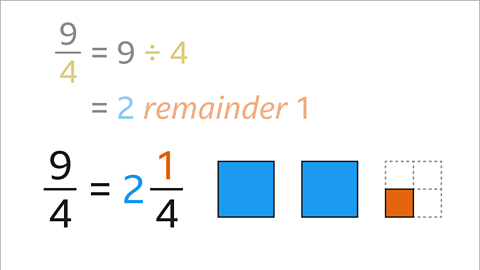
Image caption,
The whole number (2) is the integer part of the mixed number. The remainder (1) is the numerator of the fraction. 9⁄4 converts to 2 1⁄4 as a mixed number.
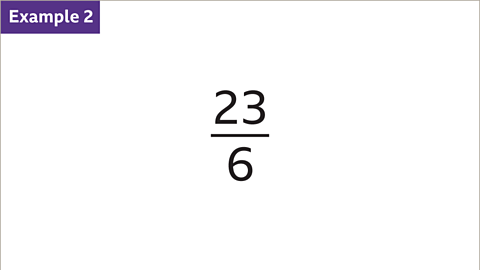
Image caption,
Convert 23⁄6 to a mixed number.
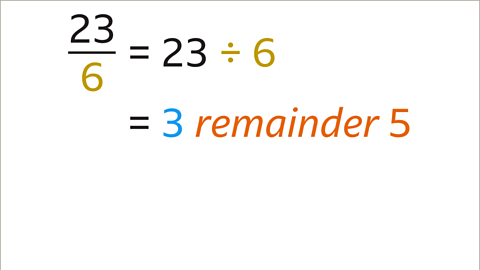
Image caption,
Divide the numerator (23) by the denominator (6). 23 ÷ 6 = 3 remainder 5. The whole number (3) is the integer part of the mixed number.
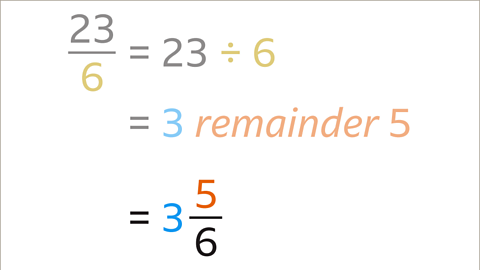
Image caption,
The remainder (5) is the numerator of the fraction. The denominator stays the same. 23⁄6 converts to 3 5⁄6 as a mixed number.

Question

Convert $ \frac{32}{5} $ to a mixed number.

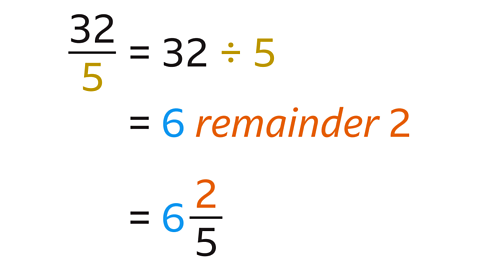
Practise converting mixed numbers and improper fractions

Try practising recognising and converting mixed numbers and improper fractions with this quiz. You might need a pen and paper to solve some of these questions.

Quiz

Real-world maths

Image caption,
Mixed numbers are often seen on road signs.

Mixed numbers and improper fractions are often used in the real-world.

For example, motorway road signs usually give distances as whole numbers.

However, road signs on smaller roads or signposts on rural routes will often use mixed numbers as the distances are much shorter.

Converting between mixed numbers and improper fractions can be used when considering things like ordering food and deciding how many pizzas you need to order for a friend’s party.

Each person wants $ \frac{1}{3} $ of a pizza. If there are 20 people, that is $ \frac{20}{3} $of pizza.
To work out how many pizzas to buy, it is helpful to convert the improper fraction into a mixed number.
20 ÷ 3 = 6 remainder 2. So $ 6 \frac{2}{3} $ pizzas are needed.
To have enough pizza for the party, you need to buy 7 pizzas.