Key points about rotation

A rotationA transformation of a shape which results in a turning effect on the shape. is one of the four types of transformation.
A rotation has a turning effect on a shape. The resulting shape is congruentShapes that are the same shape and size, they are identical. to the original shape.
The rotation turns a shape around a fixed point called the centre of rotationA fixed point about which a shape is rotated..
This point can be inside the shape, a vertexThe point at which two or more lines cross. The corner of a shape. The plural form is vertices. of the shape or outside the shape.
Rotations can be clockwiseTravelling in the same direction as the hands on a clock. or anti-clockwiseTravelling in the opposite direction to the hands on a clock. and a multiple of 90° (90°, 180° or 270°) is used.
To describe a rotation fully, specify the angle of rotation, the direction and the point it has been rotated about.
To understand rotations, make sure you are confident in working with angles and rotational symmetry.
Check your understanding
How to rotate a shape on a grid
Watch the example below
Read the steps below to see the full method outlined.
A piece of tracing paper can be useful when plotting a rotation on a grid.
To work out the position of a new shape after rotation:
Place the tracing paper over the shape.
Copy the shape on to the tracing paper.
Rotate the tracing paper in the correct direction and the specified angle, keeping the centre of rotation fixed. Use the pencil as a pivot for this.
The tracing paper now shows the position of the new shape.
Remove the tracing paper and draw the shape in its new location.
GCSE exam-style questions
- Shape 𝐴 is rotated 90° anti-clockwise about the centre of rotation, 𝑃.
Work out the new position of the image using paper, a pencil and a ruler.
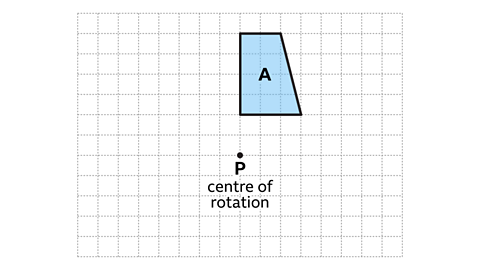
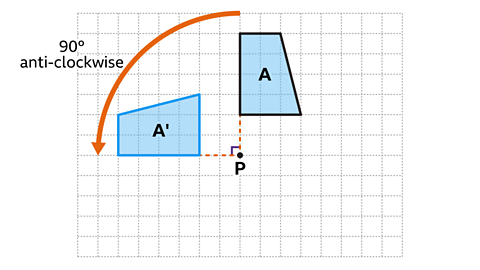
Shape 𝐴' shows the correct position of shape 𝐴 after a rotation 90° anti-clockwise about the centre of rotation, 𝑃.
- Triangle 𝑋𝑌𝑍 is rotated 180° clockwise about the centre of rotation, 𝑃.
Work out the new position of the images using paper, a pencil and a ruler.
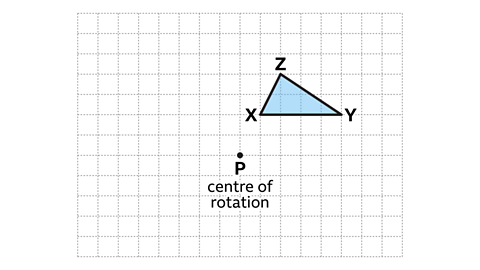
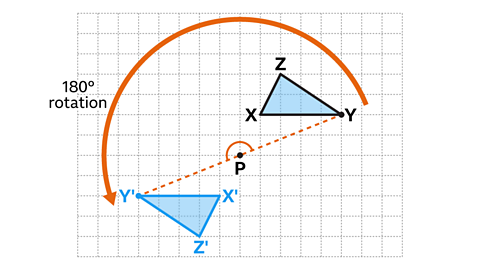
For a 180° rotation, it doesn't matter if you choose clockwise or anti-clockwise.
Triangle 𝑋'𝑌'𝑍' shows the correct position of triangle 𝑋𝑌𝑍 after a rotation of 180° around the centre of rotation, 𝑃.
Lines 𝑌𝑃 and 𝑌'𝑃 are equal in length and make an angle equivalent to the rotation, 180°.
How to rotate a shape on a set of axes
The process for rotating a shape on a set of axes is the same as on a grid.
The centre of rotation is often the originThe reference point in a coordinate system from which all other measurements are taken. This point has the coordinates (0,0)., although another point can be used.
A piece of tracing paper can be useful when plotting a rotation. It can be requested in the GCSE exam.
Follow the worked example below
GCSE exam-style questions
- Shape 𝑊 is rotated 90° clockwise about the origin.
Work out the position of the new image using paper, a pencil and a ruler.
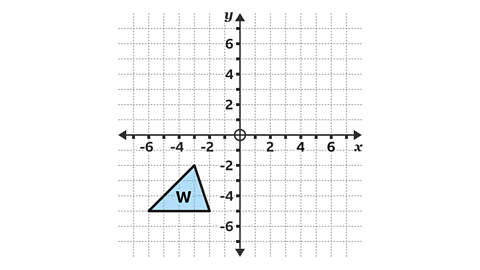
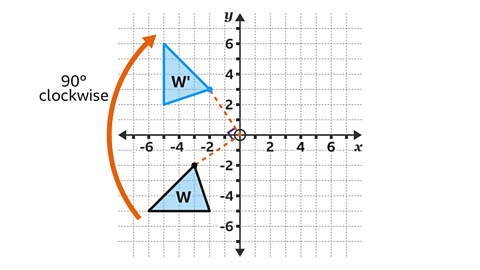
Shape 𝑊' shows the correct position of shape 𝑊 after a rotation of 90° clockwise about the origin.
The line from the origin to the point (– 3, – 2) is the same length as the line from the origin to the corresponding image point in the rotation (– 2, 3).
These lines intersect at 90°, which is the angle of the rotation.
- Shape 𝑄 is rotated 270° anti-clockwise about the point (0, 3).
Work out the position of the new image using paper, a pencil and a ruler.
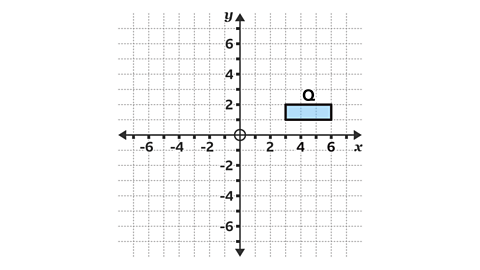
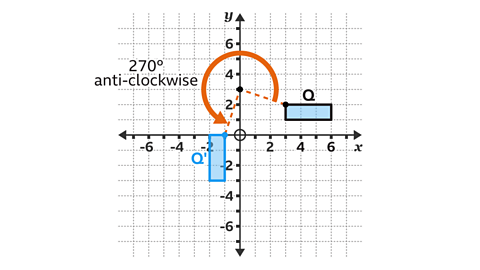
Shape 𝑄' shows the correct position of shape 𝑄 after a rotation of 270° anti-clockwise about the point (0, 3).
A rotation of 270° anti-clockwise is equivalent to a 90° clockwise rotation.
The line from the centre of rotation to the point (3, 2) is the same length as the line from the centre of rotation to the corresponding image point in the rotation ( – 1, 0).
How to describe a rotation
When describing a rotation:
- state that the transformation is a rotation
- specify the angle of rotation and direction, clockwise or anti-clockwise
- give the coordinates for the centre of the rotation
For example, the transformation could be described as being 90° clockwise rotation about the point (2, 1).
Finding the correct coordinates for the centre of rotation can be challenging but this can easily be checked using a piece of tracing paper.
Remember that the distance from the centre of rotation to the vertices of the original shape and the corresponding vertices on the rotated shape are equal.
Follow the worked example below
GCSE exam-style questions
- Shape 𝐷 is a transformation of shape 𝐶.
Describe the transformation.
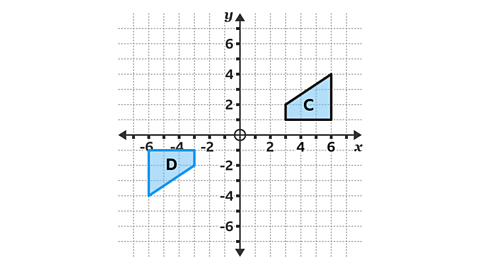
Shape 𝐷 is a rotation 180° about the origin.
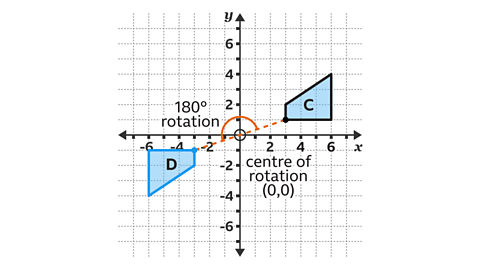
The distance from the origin to the vertices of the original shape and the corresponding vertices on the rotated shape are equal.
The lines intersect at 180°, the angle of the rotation.
- Shape 𝑄 is a transformation of shape 𝑃.
Describe the transformation.
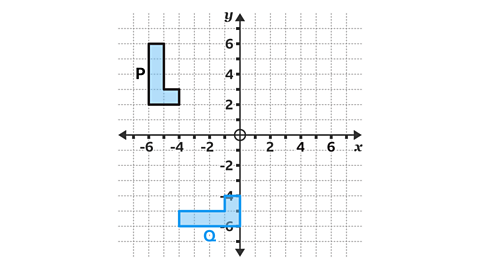
The transformation is a rotation.
Shape 𝑄 is a rotation 90° anti-clockwise about the point (1, 1).
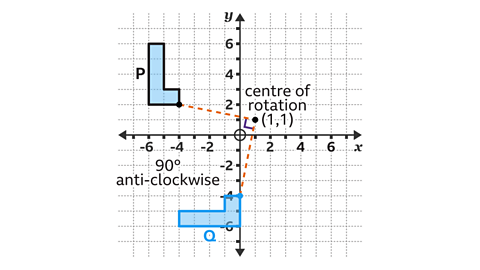
The distances from the centre of rotation to the vertices of the original shape and the corresponding vertices on the rotated shape are equal.
The lines intersect at 90°, the angle of the rotation.
Quiz – rotation
Practise what you've learned about rotation with this quiz.
Now you've revised rotation, why not look at right-angled trigonometry?
More on Geometry and measure
Find out more by working through a topic
- count21 of 30

- count22 of 30

- count23 of 30
