Key points

To solve equationA mathematical statement showing that two expressions are equal. The expressions are linked with the symbol =, a good understanding of algebraic notationA series or system of written symbols used to represent numbers, amounts or elements in mathematics. and substituteIn algebra substitute means to replace a letter (or variable) with a number. into expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms. can be helpful.
An equation is a mathematical statement showing that two expressions are equal. The two expressions are linked with an equals symbol (=).
To solve an equation, the value of the unknown variableAn unknown value, usually represented by a letter like 𝒙 or 𝒚 must be found. In the equation 3\(x\) + 4 = 25, the unknown variable is \(x\)
The unknown variable (often the letter \(x\)) can take any value, including decimal and negative values.

Solving equations with 𝒙 on one side
An equation is like a set of scales that are in balance. The termAn element within an algebraic sentence. Elements (terms) are separated by + or - signs. on both sides are in balance because they represent the same amount or value.
To solve an equation, the value of the unknown variable needs to be found. It can be found by performing the same operation on each side of the equation until the value for \(x\) is known.
inverse operationThe opposite of a mathematical process. Eg, the inverse of × 5 is ÷ 5. The inverse operation undoes the original process. are used when deciding on the operation to use. The inverse operation for addition is subtraction and the inverse operation for multiplication is division.
Check your answer by substituting the solution back into the original equation.
Examples

Image caption, Solve the equation 3𝒙 + 4 = 25

Image caption, The unknown variable in this equation is 𝒙. To solve the equation, the value of 𝒙 needs to be found. Use the inverse operation to find the value of 𝒙. Subtracting 4 is the inverse operation to adding 4. To get the value of 3𝒙, 4 must be subtracted from both sides of the equation.

Image caption, The same operation must be applied to both sides of the equation. In this example, 4 is subtracted from both sides. 3𝒙 + 4 − 4 = 3𝒙 and 25 − 4 = 21. Subtracting 4 from both sides produces the equation 3𝒙 = 21

Image caption, The value of 3𝒙 is 21. To find the value of one 𝒙, divide both sides by 3. Dividing both sides of the equation can be written as fractions.
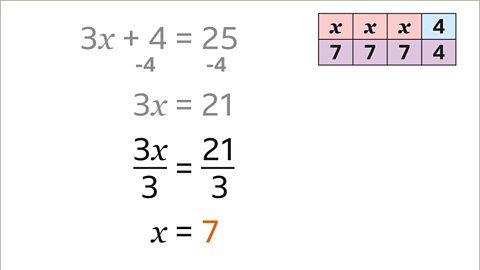
Image caption, To work out the value of 𝒙, both sides of the equation are divided by 3. 3𝒙 ÷ 3 = 𝒙 and 21 ÷ 3 = 7. Dividing both sides by 3 gives 𝒙 = 7. It is important to check your answer in the original equation. Substitute the value of 7 in the place of the 𝒙 term. If 𝒙 is 7, the statement 3𝒙 + 4 = 25 is true. The equation has been solved correctly.
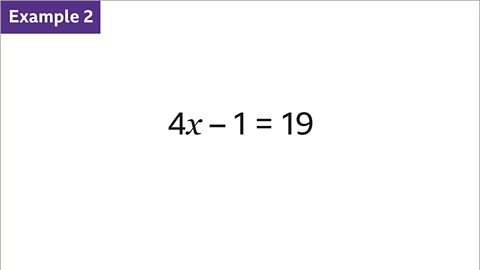
Image caption, Solve the equation 4𝒙 − 1 = 19
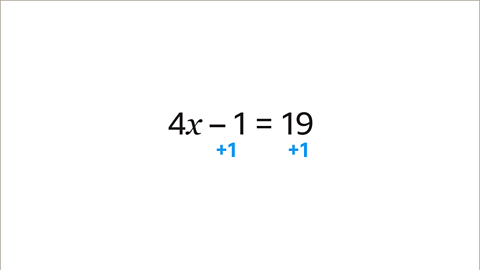
Image caption, The unknown variable in this equation is 𝒙. To solve the equation, the value of 𝒙 needs to be found. Use the inverse operation to find the value of 𝒙. Adding 1 is the inverse operation of subtracting 1. To get the value of 4𝒙, 1 must be added to both sides of the equation.
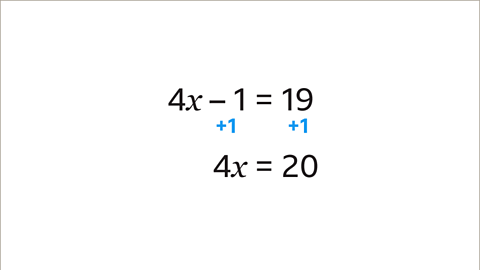
Image caption, The same operation must be applied to both sides of the equation. In this example, 1 is added to both sides. 4𝒙 − 1 + 1 = 4𝒙 and 19 + 1 = 20. Adding 1 to both sides produces the equation 4𝒙 = 20
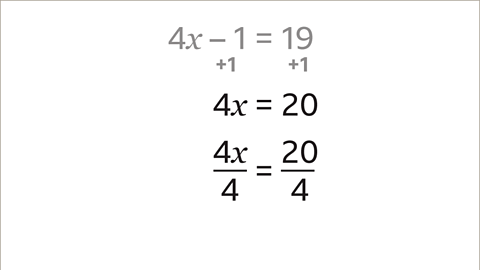
Image caption, The value of 4𝒙 is 20. To find the value of 𝒙, divide both sides by 4. Dividing both sides of the equation can be written as fractions. Dividing by 4 is the inverse operation to multiplying by 4
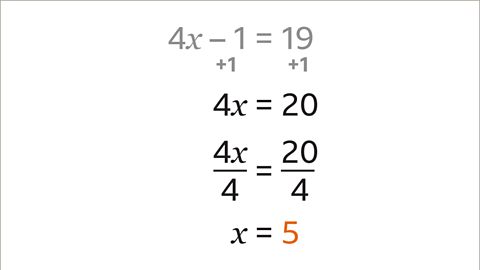
Image caption, To work out the value of 𝒙, both sides of the equation are divided by 4. 4𝒙 ÷ 4 = 𝒙 and 20 ÷ 4 = 5. Dividing both sides by 4 gives 𝒙 = 5. Check the answer by substituting 𝒙 = 5 in the original equation. 4 × 5 – 1 = 20 – 1 = 19
1 of 10
Question
Solve the equation.
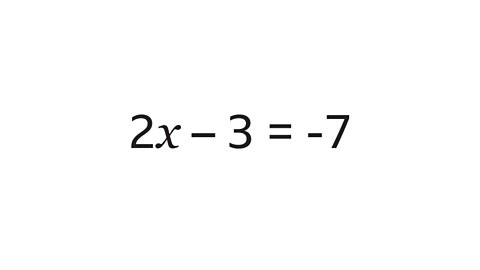
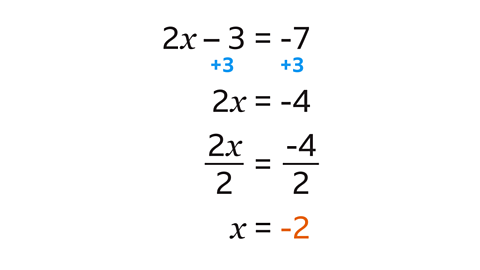
- To work out the value of \(x\), add 3 to both sides of the equation.
2\(x\) – 3 + 3 = 2\(x\) and −7 + 3 = −4
This produces the equation 2\(x\) = −4
- To find the value of \(x\), divide both sides by 2
\( \frac{2x}{2}\) \(= x\) and \( \frac{-4}{2}\) = -2
Dividing both sides by 2 gives \(x\) = −2
- Check the answer by substituting \(x\) = −2 in the original equation.
2\(x\) − 3 = −7, 2 × – 2 − 3 = –4 − 3 = −7
This proves that the solution \(x\) = −2 is correct.
Select the correct first step to solve these equations
Practise solving equations with 𝒙 on one side by selecting the correct first step.
Solving equations with two or more steps
To solve any equation, you need to find the value of the unknown variable by performing the same operations on both sides.
To solve an equation, more than one step may be needed to find the unknown variable.
Remember to check your answer by substituting the solution back into the original equation.
Examples
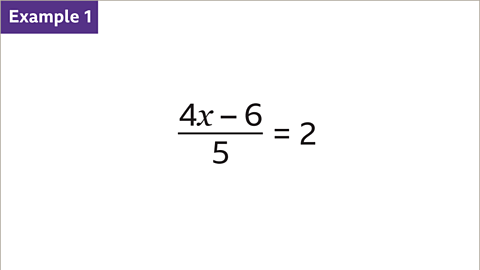
Image caption, Solve the equation.
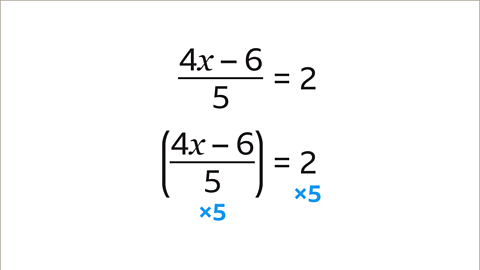
Image caption, The unknown variable in this equation is 𝒙. To solve the equation, the value of 𝒙 needs to be found. Use the inverse operation to find the value of 𝒙. Multiplying by 5 is the inverse operation to dividing by 5. To get the value of 4𝒙 - 6, both sides must be multiplied by 5
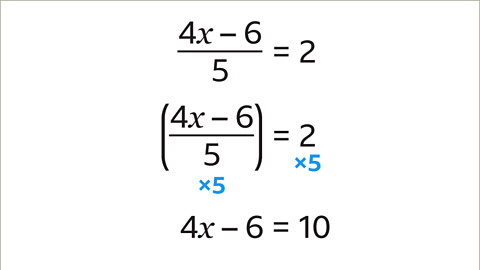
Image caption, The same operation must be applied to both sides of the equation. 4𝒙 – 6 divided by 5 multiplied by 5 is 4𝒙 – 6 and 2 multiplied by 5 is 10. Multiplying both sides by 5 produces the equation 4𝒙 – 6 = 10
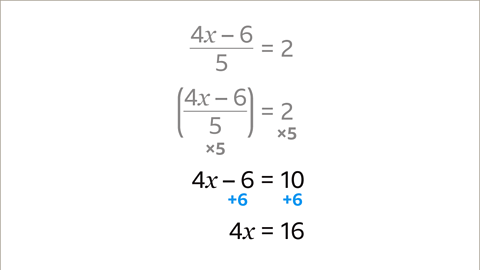
Image caption, 4𝒙 – 6 = 10. Adding 6 is the inverse operation to subtracting 6. To find the value of 𝒙, 6 must be added to both sides. 4𝒙 – 6 + 6 = 4𝒙 and 10 + 6 = 16. Adding 6 to both sides produces the equation 4𝒙 = 16
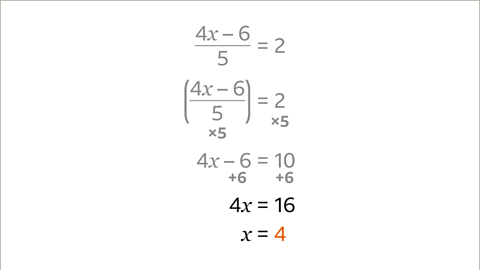
Image caption, The value of 4𝒙 is 16. To find the value of 𝒙, divide both sides by 4. 4𝒙 ÷ 4 = 𝒙 and 16 ÷ 4 = 4. The value of 𝒙 is 4. Check the answer by substituting 𝒙 = 4 in the original equation. The equation is correct.
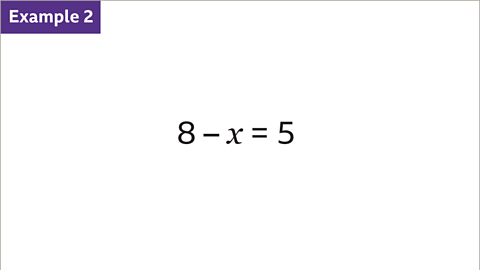
Image caption, Solve the equation.
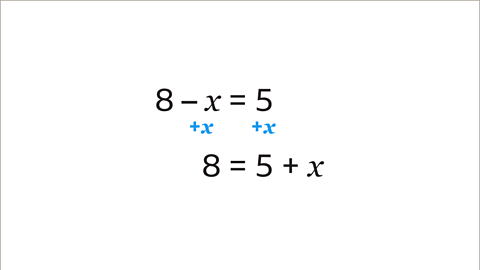
Image caption, In this equation, the unknown variable is 𝒙. To solve the equation, the value of 𝒙 needs to be found. Use the inverse operation to find the value of 𝒙 . Adding 𝒙 is the inverse operation of subtracting 𝒙. If there is a negative sign in front of 𝒙, a useful technique is to add the 𝒙 term to both sides of the equation. 8 – 𝒙 + 𝒙 = 8 and 5 + 𝒙 = 5 + 𝒙
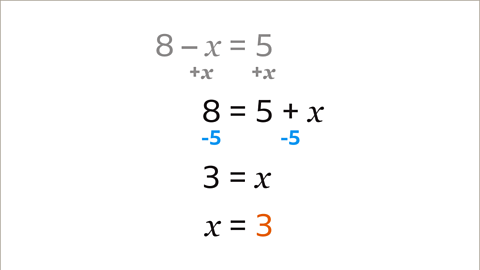
Image caption, The equation 8 = 5 + 𝒙 can be solved by subtracting 5 from both sides of the equation. 8 − 5 = 3 and 5 + 𝒙 − 5 = 𝒙. The value of 𝒙 is 3. Remember to check your answer by substituting the solution back into the original equation. If 𝒙 is 3, the statement is true. The equation has been solved correctly.
1 of 8
Question
There is a number, (\(n\)).
6 is added and then the result is multiplied by 2
The answer is 14
Write down the correct equation for this example.
Remember that in an equation, the unknown variable can take any value. In this example, the unknown variable is \(n\)
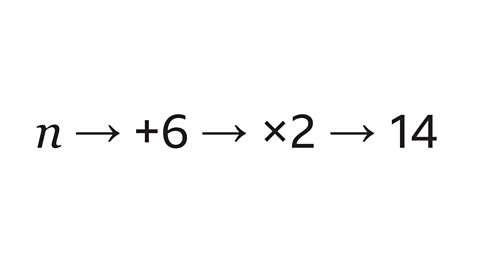
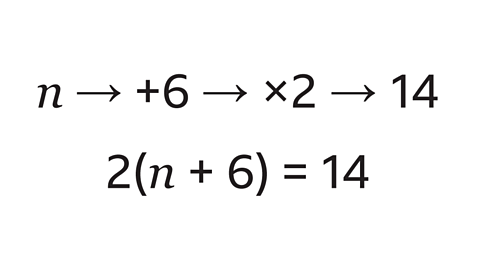
First, 6 is added to \(n\) to give \(n\) + 6
The result \(n\) + 6 is multiplied by 2
Brackets are essential to show that \(n\) + 6 is all multiplied by 2
The correct equation for this example is 2(\(n\) + 6) = 14
Practise solving equations with 𝒙 on one side
Quiz
Practise solving equations with \(x\) on one side with this quiz. You may need a pen and paper to help you with your answers.
Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Equations
Find out more by working through a topic
- count2 of 7
- count3 of 7
- count4 of 7
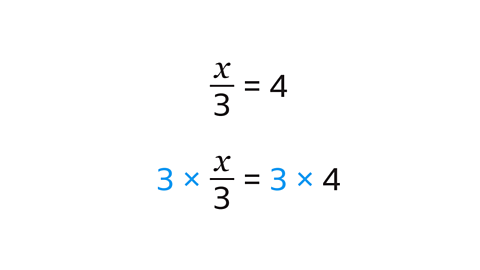
- count5 of 7
