Key points
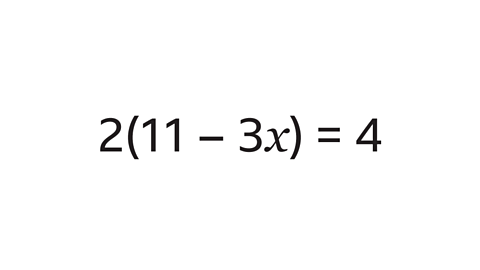
An understanding of expanding brackets is essential when solving equations with brackets.
An equationA mathematical statement showing that two expressions are equal. The expressions are linked with the symbol = is like a set of scales that are in balance. The termAn element within an algebraic sentence. Elements (terms) are separated by + or - signs. on either side of the equals symbol (=) have the same value as each other.
The equation needs to stay in balance. To keep the equation balanced, the same thing needs to be done to both sides.
Some equations have brackets. expanding Expand means to multiply to remove the brackets. these brackets makes the equation easier to solve.
Expanding brackets does not change the value of an expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms.. It is two ways of writing the same expression.
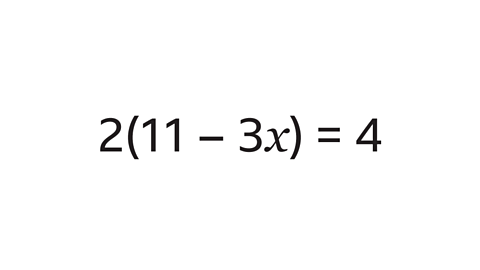
Solving equations with brackets
Some equations include a set of brackets. When solving equations with brackets the first step is to expand the brackets.
When multiplying expressionA mathematical sentence expressed either numerically or symbolically made up of one or more terms. in brackets, make sure that everything inside the bracket is multiplied by the term (or number) outside the bracket.
Expand the brackets to produce an equivalentThe same as but in a different form. equation.
simplify (equation)An equation can be simplified so it is easier to solve. Common ways to simplify equations include combining like terms and expanding brackets. the equation to isolate the \(x\) term.
Divide both sides by the coefficient of \(x\) to find the value of \(x\)
Example
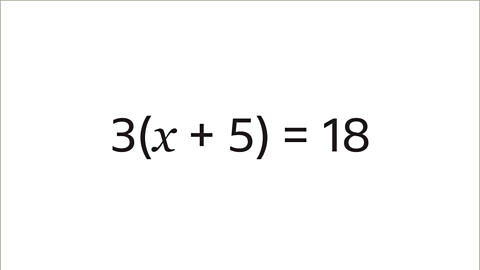
Image caption, Solve the equation 3(𝒙 + 5) = 18
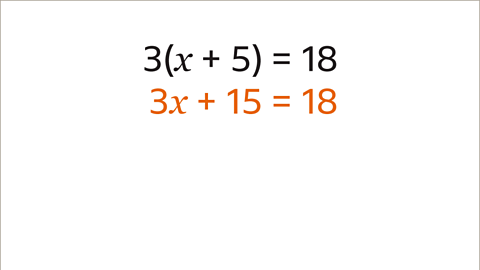
Image caption, Expand the brackets on the left hand side of the equation. 𝒙 multiplied by 3 is 3𝒙. +5 multiplied by 3 is +15. The 18 is outside the bracket so remains as 18. The equation is now 3𝒙 + 15 = 18
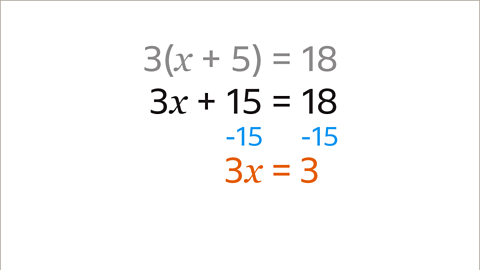
Image caption, Subtract 15 from both sides. The equation is simplified to 3𝒙 = 3. The 𝒙 term has now been isolated.
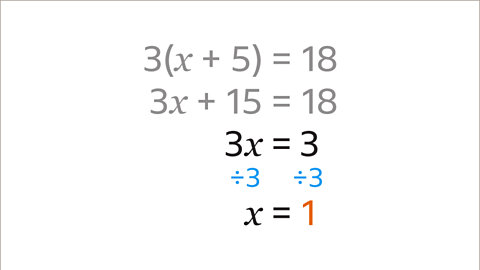
Image caption, 𝒙 multiplied by 3 is 3. Divide both sides by the 3 (the coefficient of 𝒙). The equation shows that 𝒙 = 1
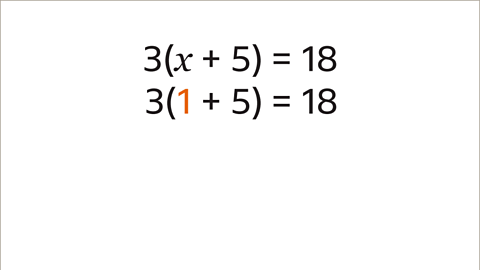
Image caption, It is important to check the answer. The original equation stated that 3(𝒙 + 5) = 18. Substitute the value of 1 in place of the 𝒙 term.
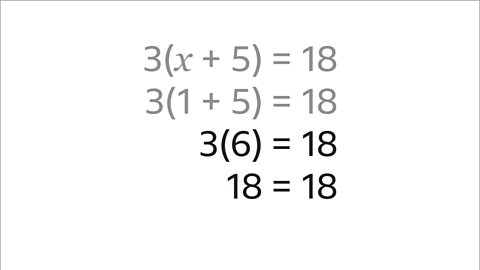
Image caption, The solution is 𝒙 = 1. When 𝒙 is 1 then the value inside the brackets is 6. Multiply the value outside the brackets (3) with the value inside the brackets, 3 x 6 = 18. This confirms that the solution of 𝒙 = 1 is correct.
1 of 6
Question
Solve the equation 3(2\(x\) + 4) = 36
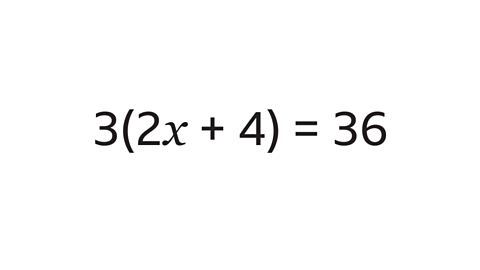
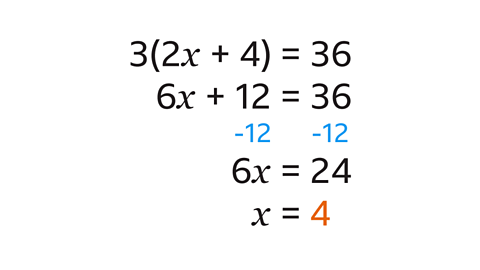
Expand the brackets to produce the new equation of 6\(x\) + 12 = 36
Isolate the \(x\) term by subtracting 12 from each side to give 6\(x\) = 24
Divide both sides by the coefficient of \(x\) (6).
This gives a solution of \(x\) = 4
Check the solution by substituting 4 back into the original equation.
Solving equations where the coefficient of 𝒙 is negative
When solving equations using brackets, the coefficient of \(x\) may be negative.
The first step is to expand the brackets, taking care where negatives are involved.
manipulateTo use or change information, for a specific purpose. Usually to reduce the number of terms in an expression or equation. the equation so that the coefficient of the unknown term is positive.
Simplify the equation to isolate the \(x\) term.
Divide by the coefficient of \(x\) to find the solution.
Check your solution by substituting your answer into the equation.
Example
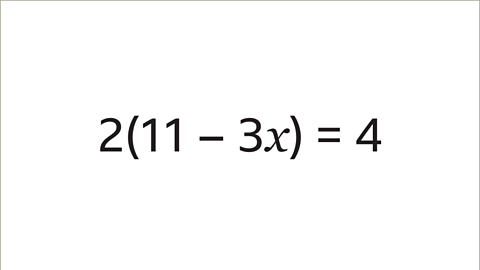
Image caption, Solve the equation 2(11 – 3𝒙) = 4
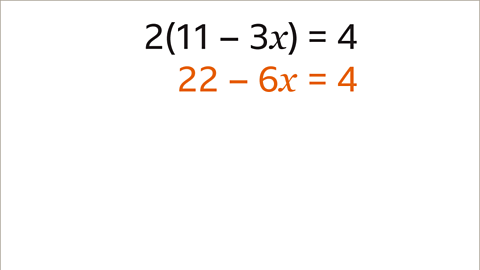
Image caption, Expand the brackets on the left-hand side of the equation. 11 multiplied by 2 is 22. -3𝒙 multiplied by 2 is -6𝒙. The 4 is outside the bracket so remains as 4. The equation now reads as 22 – 6𝒙 = 4
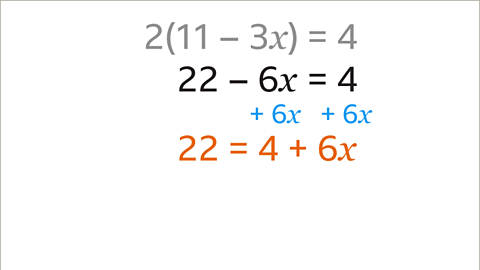
Image caption, The coefficient of 𝒙 is negative (-6). Adding 6𝒙 to both sides of the equation keeps it in balance but makes sure that the coefficient of the unknown term is positive. The equation now reads as 22 = 4 + 6𝒙
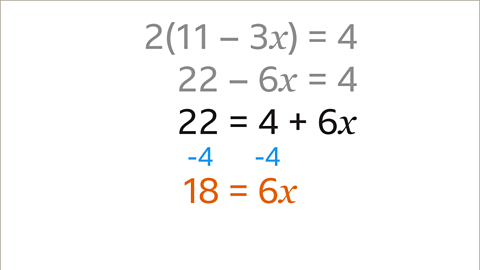
Image caption, Isolate the 𝒙 term by subtracting 4 from both sides. The equation now reads as 18 = 6𝒙
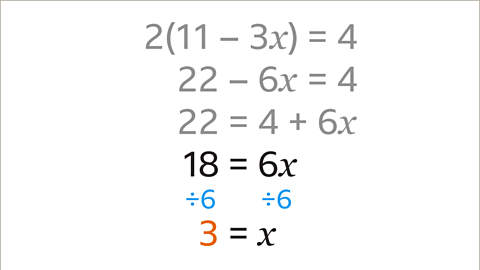
Image caption, 𝒙 multiplied by 6 = 18. Divide both sides by the 6 (the coefficient of 𝒙). The equation shows that 𝒙 = 3
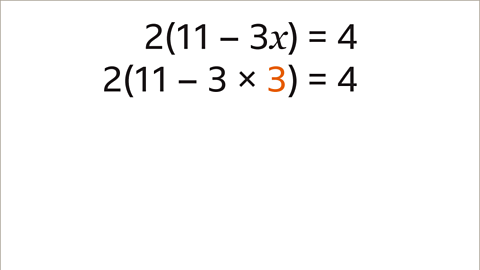
Image caption, It is important to check the answer. The original equation stated that 2(11 – 3𝒙) = 4. Substitute the value of 3 in place of the 𝒙 term.
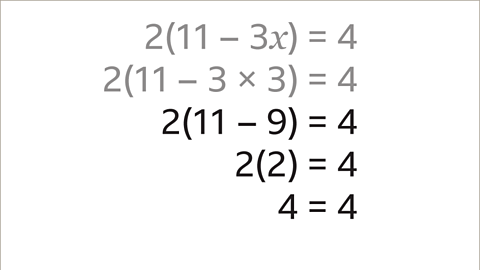
Image caption, When 𝒙 = 3, the equation becomes 2(11 – 3 × 3) = 4. The calculation inside the brackets is now 11 – 9, so the value inside the brackets is 2. Multiply the value outside the brackets (2) with the value inside the brackets (2). 2 × 2 = 4. When 𝒙 has a value of 3, then both sides of the equation are equal. This confirms the solution that 𝒙 = 3
1 of 7
Question
Solve the equation 3(11 − 2\(x\)) = 15
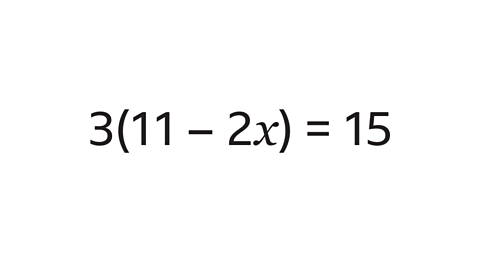
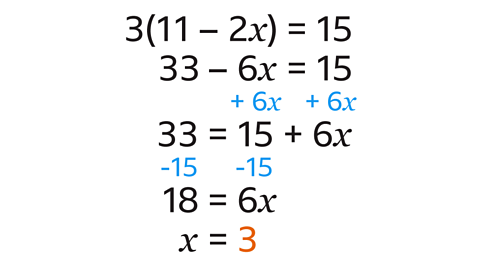
- Expand the brackets to produce the new equation of 33 − 6\(x\) = 15
- Add 6\(x\) to both sides of the equation.
- The equation simplifies to 33 = 15 + 6\(x\)
- Isolate the \(x\) term by subtracting 15 from each side to give 18 = 6\(x\)
- Divide both sides by the coefficient of \(x\) (6).
This gives a solution of \(x\) = 3
Check the solution by substituting 3 back into the original equation.
Practise solving equations with brackets
Quiz
Practise solving equations with brackets with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths
A pharmacist might use an equation involving brackets to calculate the correct amount of medicine needed for a patient according to their age.
If a pharmacist needed to work out the correct dose for an eight-year-old child, when the adult dose is 200 mg, they can use ‘Young’s formula’ to help them:
Child’s dose = Adult’s dose × (\( \frac{age}{age + 12} \))

If \(x\) represents the child’s dose, then:
\(x\) = 200 × (\( \frac{8}{8 + 12} \))
\(x\) = 200 × (\( \frac{8}{20} \))
\(x\) = 200 × 0.4
\(x\) = 80
The correct dose for the eight-year-child would be 80 mg.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Equations
Find out more by working through a topic
- count4 of 7
- count5 of 7

- count6 of 7
- count7 of 7
