What is density?
Density describes how closely packed the particles are in a solid, liquid or gas.
Key fact:densityA measure of compactness and the ratio of mass to volume. It is usually measured in kilograms per metre cubed (kg/m³) or grams per centimetre cubed (g/cm³). is the amount of massThe amount of matter an object contains. Mass is measured in kilograms (kg) or grams (g). per unit volumeThe volume of a three-dimensional shape is a measure of the amount of space or capacity it occupies, eg an average can of fizzy drink has a volume of 330 ml..
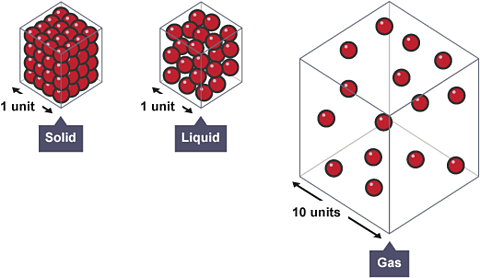
Solids, liquids and gases
All matterSub-atomic particles and anything made from them, such as atoms and molecules, are matter. Energy and forces are not matter. contains particles. The difference between the different states of matter is how the particles are arranged:
- In a solid: particles are tightly packed in a regular structure
- In a liquid: particles are tightly packed but free to move past each other
- In a gas: particles are spread out and move randomly
There is little difference between the density of a liquid and its corresponding solid (e.g. water and ice). This is because the particles are tightly packed in both states. The same number of particles in a gas spread further apart than in the liquid or solid states. The same mass takes up a bigger volume - this means the gas is less dense.
Density also depends on the material. A piece of iron with the same dimensions as a piece of aluminium will be heavier because the atoms are more closely packed.
Scientists can measure how tightly packed the particles are by measuring the mass of a certain volume of the material: for example, one cubic centimetre.
| Material | Density in grams per cubic centimetre (g/cm³) |
|---|---|
| Iron | 7.8 |
| Ice | 0.98 |
| Water | 1 |
| Air | 0.0012 |
Calculating density
Density can be calculated using the equation:
\(density = \frac{mass}{volume}\)
\(p=\frac{m}{V}\)
This is when:
- density (p) is measured in kilograms per metre cubed (kg/m3)
- mass (m) is measured in kilograms (kg)
- volume (V) is measured in metres cubed (m3)
Example
What is the density of a material if 0.45 cubic metres (m3) of it has a mass of 0.2 kg?
\(p = \frac{m}{V}\)
\(p = \frac{0.2}{0.45}\)
\(p = 0.44~kg/m^{3}\)
Units of density
Although the standard unit for mass is kilograms (kg) and for volume is cubic metres (m3), in many laboratory situations it is usual to to find the mass in grams (g) and volume in cubic centimetres (cm3).
Calculating density using grams and centimetres cubed would give a density unit of grams per centimetre cubed (g/cm3).
Question
What is the density of a material if 15 cm3 of it has a mass of 30 g?
\(p=\frac{m}{V}\)
\(p=\frac{30}{15}\)
\(p = 2~g/cm^3\)
Key fact: 1 g/cm3 is equal to 1,000 kg/m3
- To convert from kg/m3 to g/cm3, divide by 1,000.
- To convert from g/cm3 to kg/m3, multiply by 1,000.
Aluminium has a density of 2.7 g/cm3, or 2,700 kg/m3. Lead has a density of 11.3 g/cm3, or 11,300 kg/m3.
Iron has a density of 7.9 g/cm3. What is this in kg/m3?
7.9 multiplied by 1,000 gives 7,900 kg/m3.
Question
What is the density of an object in kg/m3 if it is 653.1g/cm3?
653.1 multiplied by 1,000 gives 653,100 kg/m3.
Video: Density calculation with an experiment
Jonny Nelson explains density with a GCSE Physics practical experiment.
JONNY NELSON:
Hamsters.
What do they have to do with density?
Nothing, but hamsters are pretty cute, and attaching them to helium balloons means that we can get them into this video.
So why does Frieda, the hamster, float?
Because the helium atoms in the balloons have a much smaller mass than the mainly nitrogen and oxygen molecules in the air around them.
This makes the helium balloon less dense than the surrounding air.
The lower density of the balloon means its upthrust is greater than its weight.
The overall force is upwards, so the helium balloon can lift the weight of little Frieda here, which causes her to float.
If Frieda was too heavy, the basket wouldn't float and she would fall to the ground.
Better not eat too much then, eh, Frieda?
[Explaining Density]
Density is mass per unit volume.
Basically, it's how much mass there is in each metre cubed of an object.
To calculate density, all we need is the mass of an object in kilograms and its volume in cubic metres.
Finding the volume of an object depends on whether it's a regular or irregular object.
To calculate the volume of this regular object (a cuboid), just multiply the three dimensions: width, height, and depth (measured in metres) together.
In this case, the volume is 0.000125 cubic metres.
Weigh an object to find its mass, making sure that it is in kilograms.
This regular object: 0.093kg.
If the object is irregular, a simple experiment can find its volume.
You will need:
- a Eureka or displacement can
- a measuring cylinder
- some water
- a top pan balance
- and an object
We'll be using this plastic penguin which has a mass of 0.035kg.
Fill the Eureka can full of water, and when the object is added to the can, the volume of the water that is displaced and therefore flows out of the can must be the same as the volume of the object.
Our penguin has displaced 25ml of water, but the volume of water displaced from the can needs to be measured in cubic metres for the equation.
So it needs to be converted from millilitres to cubic metres.
Once we've done that, we can see that the volume of the penguin is 0.000025 metres cubed.
Right, now we know both the masses and both volumes.
So Eureka! We can work out the densities.
Density is the amount of mass per cubic metre, or as an equation: Density (kg/m³) = Mass (kg) ÷ Volume (m³)
If the mass of an object stays the same but the object increases in volume, its density would decrease.
And if its mass increases but its volume stays constant, its density would increase.
We have already measured the mass of our objects and we've worked out their volume.
Now all we need to do is calculate their densities using the equation: Density = Mass ÷ Volume
So the density of our regular object is 744 kg/m³, and the density of our penguin friend is 1400 kg/m³.
And this is how you calculate density, eh, Frieda?
Question
What is the density of a metal if 4 cubic metres (m3) of it has a mass of 2,200 kg?
\(p=\frac{m}{V}\)
\(p=\frac{2,200}{4}\)
\(p = 550~kg/m^3\)
Calculating volume to find density
Method one: Regular solid cube and sphere
To calculate density, the volume of the material must be known. If the object is a regular shape, the volume can be found by using a ruler and one of the equations below.
| Shape | Measurements | Equation |
|---|---|---|
| cube | length (l), width (w), height (h) | \(lwh\) |
| sphere | diameter (d) | \(\frac {4}{3} \pi (\frac{d}{2})^3\) |
| cylinder | diameter of base (d), length of cylinder (l) | \(\pi(\frac{d}{2})^2~l\) |
| cone | diameter of base (d), length of cone (l) | \(\pi (\frac{d}{2})^2~\frac{l}{3}\) |
If the object has an irregular shapeA shape with unequal side lengths., the volume can be measured using a displacement canA piece of equipment to measure the volume of an irregular solid. The can is filled with water up to a narrow spout and the solid placed in the can. The water displaced through the spout is collected and its volume measured - this is equal to the volume of the solid..
The displacement can is filled with water above a narrow spoutA tube or lip that allows liquid to flow or pour from a container. and allowed to drain until the water is level with the bottom of the spout.
As the irregular object is lowered into the displacement can, the water level rises. All the displaced water comes out of the spout and is collected in a measuring cylinderA piece of equipment used to measure the volume of a liquid. .
The displacedMoved out of position. For example, an object placed in a beaker of water displaces the water, causing the water level to rise. water in the cylinder occupies the same amount of space as the object in the can, which means that their volumes are the same.
Practical experiment: Investigating density
There are different ways to investigate density. In this practical activity, it is important to:
- record the mass accurately
- measure and observe the mass and the volume of the different objects
- use appropriate apparatus and methods to measure volume and mass
Aim of the experiment
To measure the density of various materials.
Method 1: Regular solid cube and sphere
- Use a ruler to measure the length (l), width (w) and height (h) of a steel cube.
- Place the steel cube on the top pan balance and measure its mass.
- Calculate the volume of the cube using (l × w × h).
- Use the measurements to calculate the density of the metal.
- Use vernier callipersA measuring instrument used to find internal or external dimensions accurately eg to the nearest 0.05 mm. to measure the diameter of the sphere.
- Place the metal sphere on the top pan balance and measure its mass.
- Calculate the volume of the sphere using \(\frac{4}{3} \pi (\frac{d}{2})^3\)
- Use the measurements to calculate the density of the metal.
Method 2: Stone or other irregular shaped object
- Place the stone on the top pan balance and measure its mass.
- Fill the displacement can until the water is level with the bottom of the pipe.
- Place a measuring cylinder under the pipe ready to collect the displaced water.
- Carefully drop the stone into the can and wait until no more water runs into the cylinder.
- Measure the volume of the displaced water.
- Use the measurements to calculate the density of the stone.
Method 3: Water (or any liquid)
- Place the measuring cylinder on the top pan balance and measure its mass.
- Pour 50 cm3 of water into the measuring cylinder and measure its new mass.
- Subtract the mass in step 1 from the mass in step 2. This is the mass of 50 cm3 of water.
- Use the measurements to calculate the density of the water.
Results
Some example results could be:
| Object | Mass (g) | Volume (cm³) | Density (g/cm³) | Density (kg/m³) |
|---|---|---|---|---|
| Steel cube | 468 | 60 | ||
| Steel sphere | 33 | 4.19 | ||
| Stone | 356 | 68 | ||
| Water | 50 | 50 |
Analysis
Using those results, the densities can be calculated using: density = mass ÷ volume
Mass of steel cube = 468 g
Volume of steel cube = 60 cm3
Density = mass ÷ volume = 468 ÷ 60 = 7.8 g/cm3 (= 7,800 kg/m3)
Diameter of steel sphere = 2 cm
Mass of steel sphere = 33 g
Volume of steel sphere = \(\frac {4}{3} \pi (\frac{d}{2})^3 = 4.19~cm^3\)
Density = mass ÷ volume = 33 ÷ 4.19 = 7.9 g/cm3 (= 7,900 kg/m3)
For a stone of mass 166 g, the volume of water displaced into the measuring cylinder is 68 cm3.
Density = mass ÷ volume = 166 ÷ 68 = 2.4 g/cm3 (= 5,200 kg/m3)
Mass of 50 cm3 of water is found to be 50 g.
Density = mass ÷ volume = 50 / 50 = 1 g/cm3 (= 1,000 kg/m3)
Evaluation
- Density can be measured for regular solids, irregular solids and liquids
- Densities calculated from measurements are subject to experimental error. This could be because:
- the top pan balances used by different people may not be identically calibrated
- the resolution of the measuring cylinders may be different, causing different values for the volume to be recorded
- the displacement can may not have been set up correctly each time and any additional drops of water would cause some to dribble out of the spout before use
- The experiment above shows steel to have two different values for density: 7.8 g/cm3 and 7.9 g/cm3. This may be because some measurements are taken to different numbers of significant figures and this can create rounding errors, so the last significant figures differ. But it can also mean that the actual value is between 7.8 g/cm3 and 7.9 g/cm3
Hazards and control measures
| Hazard | Consequence | Control measures |
|---|---|---|
| Water spilled from displacement can | Slip and fall | Use a measuring cylinder to collect displaced water and prevent spills |
Density and floating

An object or a liquid will float if it is less dense than the liquid beneath it.
Ice floats on top of water because the density of ice (900 kg/m3) is less than the density of water (1000 kg/m3). A ship floats on water because the average density of the ship (metal from which it is made, cargo, people and air contained within it) is less than 1000 kg/m3.

Question
Balsa wood has a density of 160 kg/m3. Oak has a density of 750 kg/m3. Water has a density of 1000 kg/m3. Would the balsa wood and the oak float or sink?
Both the balsa wood and the oak would float because both have a density less than that of water.
Extended syllabus content
If you are studying the Extended syllabus, you will also need to know about the density of liquids. Click 'show more' for this content:
Liquids have different densities.
For example, oil is less dense than water, but syrup is more dense than water.
Key fact: A less dense liquid will float on top of a denser liquid.
Salt water is denser than fresh water, so a ship will float higher in the salty sea than in the fresh water of a river.
Experiment: Densities of liquids
You can make your own experiment to explore the different densities of liquids.
You will need:
- golden syrup
- water
- cooking oil
- a tall jar
Add each liquid slowly to the jar so that they don’t mix.
Which liquid is the most dense? Which liquid is the least dense?
Question
Golden syrup has a density of 1430 kg/m3. Water has a density of 1000 kg/m3. Which would sink to the bottom of the container?
Answer
Golden syrup would sink to the bottom of the container because it is more dense than water.

Quiz
Test your knowledge with this quiz on the density of materials.
More on Motion, forces and energy
Find out more by working through a topic
- count5 of 11

- count6 of 11

- count7 of 11

- count8 of 11
