সিস্টেরসিয়ান সংখ্যা পদ্ধতি: ইউরোপে শত শত বছর ধরে চালু যে গণনা পদ্ধতি একদম বিস্মৃত

১৯৯১ সালে লন্ডনের নিলাম প্রতিষ্ঠান ক্রিস্টি‌জের কাছে এমন এক মূল্যবান জিনিস এলো, যেটি কেবল তার সৌন্দর্যের জন্য নয়, বরং এটির উপর খোদাই করা রহস্যময় প্রতীকের জন্যও সবার মনোযোগ কাড়লো।

এটি আসলে মধ্যযুগে জ্যোতির্বিজ্ঞানীদের ব্যবহৃত এক যন্ত্র - আমাদের পূর্বপুরুষেরা হয়তো এটি দিয়ে জ্যোতির্বিজ্ঞানের নানা হিসেব কষতেন।

ক্রিস্টিজের কাছে আসা এই যন্ত্রটি হয়তো চতুর্দশ শতকের শেষে স্পেনে তৈরি করা হয়েছিল। এরপর হয়তো এটির বহুবার হাত বদল হয়েছে।

এই যন্ত্রটি নিয়ে যেসব বিশেষজ্ঞের মধ্যে আগ্রহ তৈরি হলো, তাদের একজন ব্রিটিশ ইতিহাসবিদ ডেভিড এ কিং। তিনি উত্তর ফ্রান্সের নর্ম্যান্ডির একটি পাণ্ডুলিপিতে একই ধরণের প্রতীক দেখতে পেয়েছিলেন।

ওই পাণ্ডুলিপিটিও মধ্যযুগের একই সময়ের।

মধ্যযুগীয় শাস্ত্র এবং গণিতের ইতিহাস সম্পর্কে যারা বিশেষজ্ঞ, তাদের কাছেও এসব গাণিতিক প্রতীক একেবারেই অজানা।

ত্রয়োদশ শতকের শেষের দিকে খ্রিস্টান সন্ন্যাসীরা এই গণনা পদ্ধতি তৈরি করে। ইউরোপ-জুড়ে প্রায় সব মঠে সন্ন্যাসীরা এভাবেই সংখ্যা লিখতেন। প্রায় দু'শো বছর ধরে এই গণনা পদ্ধতি চালু ছিল।

ওই সময় আরবদের ব্যবহৃত সংখ্যা গণনার পদ্ধতি রোমান সংখ্যার জায়গা নিচ্ছিল। কিন্তু নতুন গণনা পদ্ধতি ব্যাপকভাবে চালু হতে আরও বহু শতাব্দী সময় লেগেছিল।

কিন্তু গোঁড়া খ্রিস্টান সন্ন্যাসীরা এই বিতর্কে না গিয়ে তাদের ব্যবহৃত পদ্ধতিই ধরে রাখে। পুরো ইউরোপে ইংল্যান্ড হতে ইতালি, স্পেন হতে সুইডেন - সর্বত্র সংখ্যা গণনার এই তৃতীয় বিকল্পই ব্যবহার করতে থাকে খ্রিস্টান সন্ন্যাসীরা।

এটি এত জনপ্রিয় হওয়ার কারণও ছিল। রোমান সংখ্যার চেয়ে এই পদ্ধতির একটি সুবিধা হচ্ছে, যে কোন সংখ্যাকে কেবল একটি প্রতীক দিয়েই লেখা যায়।

তবে রোমান পদ্ধতির মতো এটিরও একটি দুর্বলতা ছিল - এই পদ্ধতিতে গুণ-ভাগ করা অত সহজ ছিল না।

তারপর হাতে লেখা পাণ্ডুলিপিকে হটিয়ে যখন ছাপা বই চলে এলো, ততদিনে ০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮ এবং ৯ পৃথিবী জয় করে নিয়েছে।

আর রোমান সংখ্যা I, V, X, L, C, D এবং M ভবিষ্যতের পৃথিবীতেও জায়গা করে নিয়েছে।

কিন্তু খ্রিস্টান সন্ন্যাসীদের গণনা পদ্ধতি এমনভাবে বাতিল হয়ে গেল যে এক শতাব্দী পর তা এক ধাঁধাঁয় পরিণত হলো।

ব্রিটিশ ইতিহাসবিদ ডেভিড কিং জানান, আর সব জায়গায় বিলুপ্ত হয়ে গেলেও বেলজিয়ামের ফ্লেমিশ অঞ্চলে আঠারো শতক পর্যন্ত এসব সংখ্যা ব্যবহার করা হতো ওয়াইনের ব্যারেল চিহ্নিত করতে এবং তরল পদার্থ মাপার কাঠির স্কেলে।

গোঁড়া খ্রিস্টান সন্ন্যাসীদের ব্যবহৃত এসব সংখ্যা ইতিহাসে এরপরও কয়েকবার ব্যবহৃত হতে দেখা গেছে। ১৭৮০ সালে প্যারিসে ফ্রিম্যাসনরা এসব সংখ্যা ব্যবহার করতো।

বিংশ শতাব্দীতে জার্মান লোকগাথার জাতীয়তাবাদী লেখাতেও এর ব্যবহার দেখা গেছে।

কিন্তু এই গণনা পদ্ধতি - যাকে জার্মান রেনেসাঁ যুগের গণিতবিদ আগরিপা অব নেটেশেইম "খুবই চমৎকার সব সংখ্যা" বলে বর্ণনা করেছেন, তা কীভাবে কাজ করে?

"খুবই চমৎকার সব সংখ্যা"

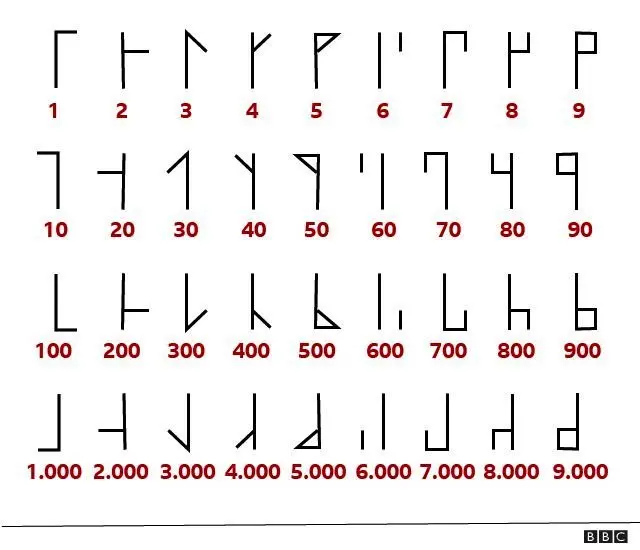
ডেভিড কিং-এর মতে, গোঁড়া খ্রিস্টান সন্ন্যাসীদের এই গণনা পদ্ধতি খুব সহজ কিছু সংখ্যার ওপর ভিত্তি করে গড়ে উঠা। ১ হতে ৯৯ পর্যন্ত প্রতিটি সংখ্যা একদম সহজ কিছু প্রতীক দিয়ে লেখা হয়।

ত্রয়োদশ শতকে এভাবে গণনা করার পদ্ধতি এথেন্স থেকে ইংল্যান্ডে নিয়ে এসেছিলেন ব্যাসিংটোকের সন্ন্যাসী জন।

সময়ের সঙ্গে এই গণনা পদ্ধতির আরও উন্নতি হয় এবং ১ হতে ৯,৯৯৯ পর্যন্ত প্রতিটি সংখ্যা একটি আলাদা প্রতীক দিয়ে লেখা যেত।

বেনেডিক্টাইন সন্ন্যাসী এবং ইতিহাসবিদ ম্যাটিও দ্য প্যারিস তার বিখ্যাত 'ক্রনিকা মেজরা' বইতে দেখিয়েছেন কীভাবে এগুলো লিখতে হবে।

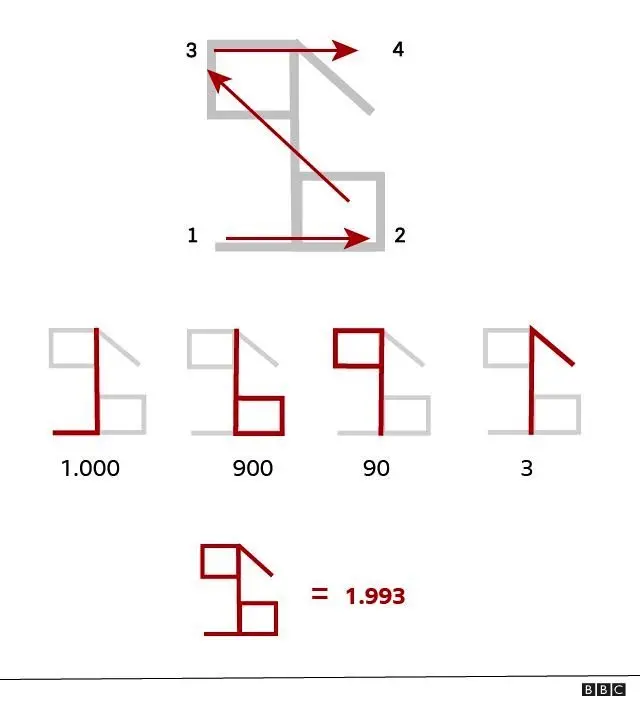
নীচের ছবিতে প্রতিটি কোনা বা চতুর্ভুজের মধ্যে হাজার (১), শতক (২), দশক (৩) এবং ইউনিট (৪) ক্রম অনুসারে আছে।

গোঁড়া সন্ন্যাসীদের মঠগুলোতে যখন এই গণনা পদ্ধতি ব্যাপকভাবে চালু হলো, তখন বিভিন্ন এলাকায় স্থানীয়ভাবে যে ভাষা বলা হতো, সেই ভাষা অনুযায়ী এতে কিছু পরিবর্তন আনা হয়েছিল।

বিবিসি বাংলায় আরও পড়ুন:

৭০ বছরের বেশি সময় ধরে যে রহস্যের জবাব খুঁজছেন গণিতজ্ঞরা

প্রাণীরাও সংখ্যা বোঝে, হিসেব করতে পারে - কিন্তু কীভাবে?

এক পর্যায়ে শুরুর লাইনটা ছিল আনুভূমিক। কিন্তু চতুর্দশ শতক নাগাদ ফরাসী সন্ন্যাসীরা এটিকে আবার আগের অবস্থানে ফিরিয়ে নেয়।

ম্যাটিও দ্য প্যারিসের মতে, এই গণনা পদ্ধতির সবচেয়ে প্রশংসনীয় দিক হচ্ছে, একটি মাত্র হরফ দিয়ে যে কোন সংখ্যা লেখা যায় - যেটা কিনা আরবী বা রোমান পদ্ধতিতে সম্ভব নয়।

তবে সমস্যা হচ্ছে একটাই - কীভাবে এগুলো পড়তে বা লিখতে শেখা যায়।

তবে মূল নিয়ম অনুসরণ করতে পারলে এটি হয়তো শুরুতে যতটা কঠিন বলে মনে হচ্ছে, ততটা কঠিন নয়।