Key points
A list of numbers or diagrams that are in a particular order is called a sequenceA sequence is a set of numbers that follow a certain rule. For example, 3, 5, 7, 9… is a sequence starting with 3 and increasing by 2 each time.
A number patternA number pattern refers to a sequence of numbers that follow a certain order in mathematics. which increases (or decreases) by the same amount each time is called a linear sequence.
The amount it increases or decreases by is known as the common differenceThe difference between successive terms in a linear sequence..
Recognising the common difference means that the sequence can be continued using a term-to-termA term-to-term rule is a rule that allows you to find the next number in a maths sequence, if you know the previous numbers (or terms)..

Finding the next term in an arithmetic sequence
- The first step is to find the common difference between common differenceThe difference between successive terms in a linear sequence. in the arithmetic sequence.
- If the arithmetic sequence is increasing, then the common difference will be to add the same amount each time.
- An arithmetic sequence can also decrease, which means that the common difference will be to subtract the same amount each time.
- Add (or subtract) the common difference to the last given number in the sequence.
Examples

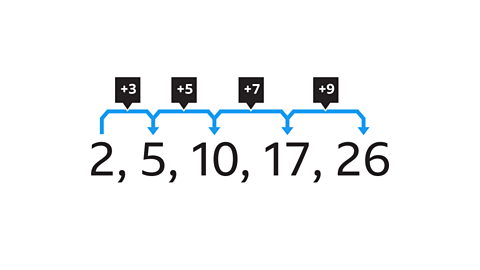
Image caption, What is the next number in the sequence?

Image caption, Look at the difference between one term and the next in the sequence. The numbers in this sequence are increasing.
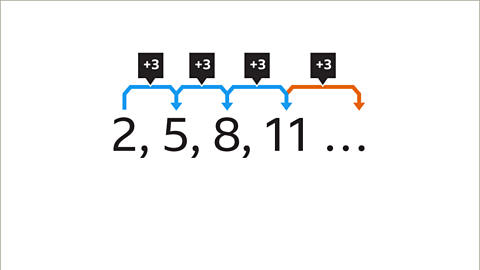
Image caption, The common difference between the terms is 3. The term-to-term rule is +3.
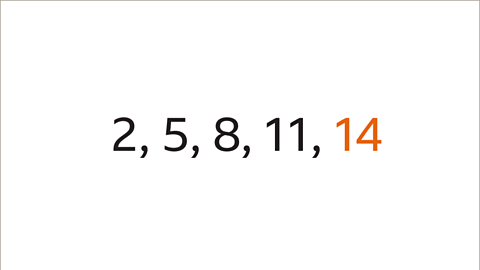
Image caption, The sequence will continue using the same term-to-term rule (+3). The next term in the sequence is 14 (11 + 3).

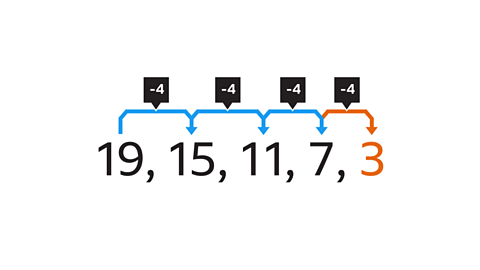
Image caption, What is the next number in the sequence?
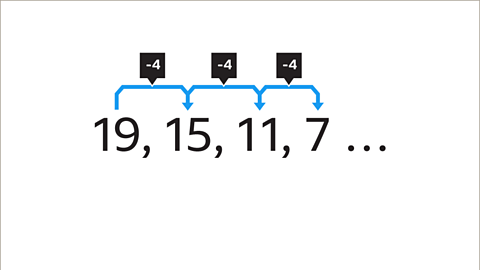
Image caption, Look at the difference between one term and the next in the sequence. In this example, the numbers in the sequence are decreasing. The term-to-term rule is -4.
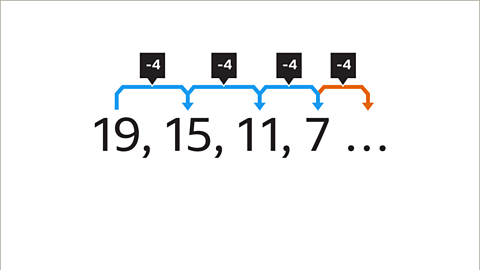
Image caption, The sequence will continue using the same term-to-term rule (-4).
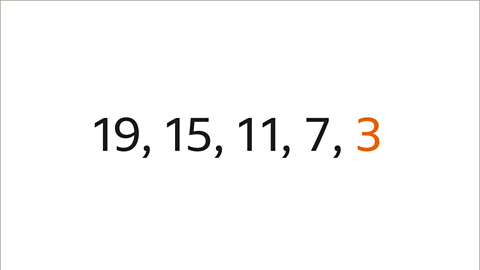
Image caption, The next term in the sequence is 3 (7 – 4).
1 of 8
Question
What is the next number in this arithmetic sequence?

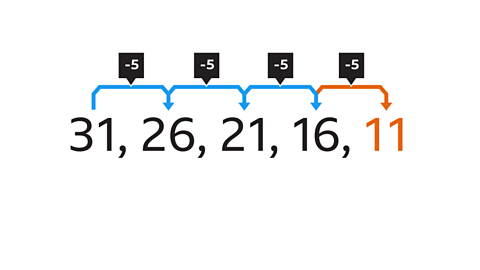
The numbers in this sequence are decreasing. The term-to-term rule is -5.The next term in the sequence is 11 (16 − 5).
Number patterns from diagrams
- Sequences can be a series of diagramA simple drawing that shows the workings out or representation of something..
- A number pattern in a diagram often requires counting shapes to find the rule.
- Look at how the pattern grows from one term to the next.
- Sometimes there are different elements (or shapes) in the diagram that decrease or increase in different ways.
- Knowing how the shapes decrease or increase makes it possible to draw the next pattern in the sequence.
Examples
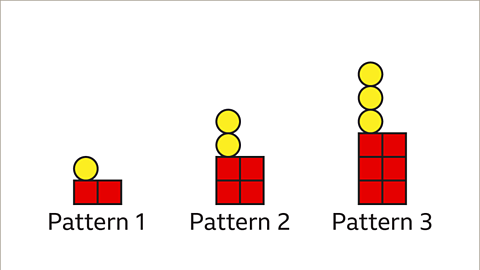
Image caption, How many yellow circles and red squares will be needed to make the next pattern in the sequence?
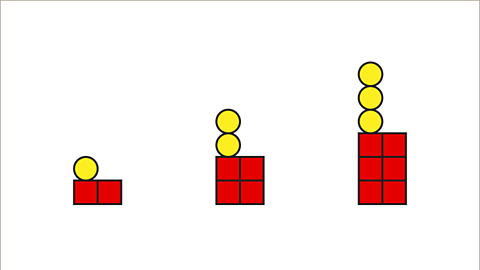
Image caption, Look at the difference between one pattern and the next in the sequence. Here, 1 yellow circle and 2 red squares are being added each time.
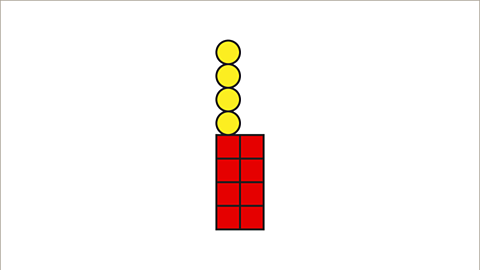
Image caption, One way to solve the problem is to sketch the next pattern.
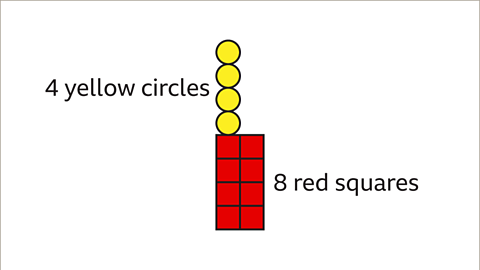
Image caption, Count the number of yellow circles and the number of red squares now present. There are 4 yellow circles. There are 8 red squares.

Image caption, Recording the number of each type of shape into a table turns the problem into a term-to-term rule question, like the ones that are shown in the examples in the first slideshow.
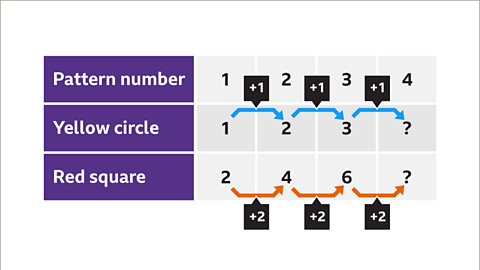
Image caption, The number of yellow circles increases by 1 each time. The number of red squares increases by 2 each time.
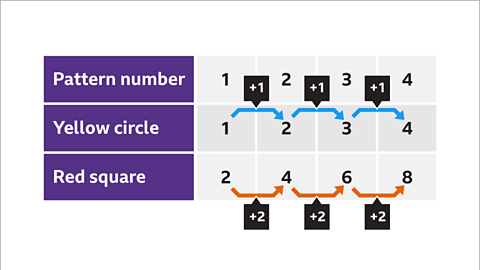
Image caption, In the next pattern, there will be 4 yellow circles and 8 red squares.
1 of 7
Question
How many red tiles will be needed to make the fourth pattern?
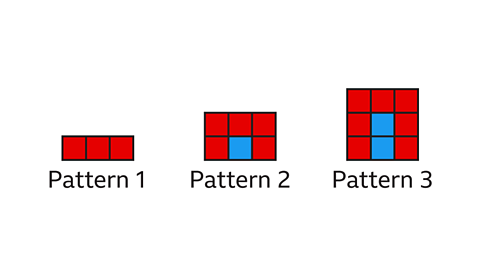
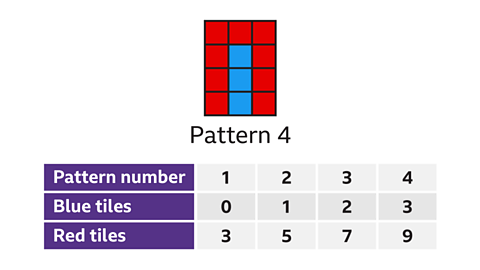
Pattern 4 will have 3 blue tiles and 9 red tiles, therefore the pattern increases by 2 red tiles and 1 blue tile each time.
Practise linear arithmetic sequences
Quiz
Practise exploring number patterns in linear sequences with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths
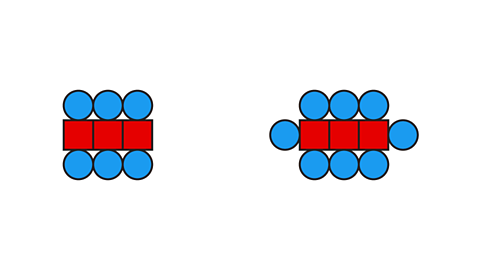
Using sequences can be helpful in everyday life.
Hospitality venues that host events can offer a variety of ways in how they set up a room. They can organise how tables and chairs should be arranged, depending on how many people are attending an event and the layout of the room.
For example, one option could be to have four guests seated around a table (represented in the image by one red block) or instead to have six guests seated around a table (represented by two red blocks).
Using the same seating arrangements, the event organiser can use similar sequences to calculate how many guests can then be seated at three tables, or more.

Play Sudoku with BBC Bitesize!
Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

More on Patterns and sequences
Find out more by working through a topic
- count3 of 4
- count4 of 4