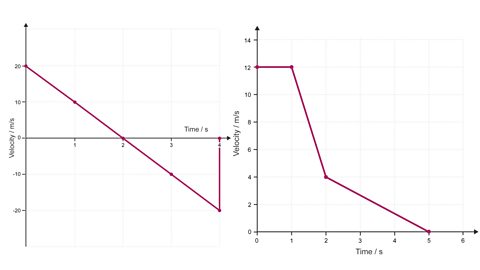
What are the key learning points about calculating motion?
To explain the difference between scalarA physical quantity that has magnitude (size) only. A scalar quantity does not have a direction. Examples: distance, speed, mass, time, energy, temperature. and vectorA physical quantity that has magnitude (size) and direction. Examples: displacement, velocity, acceleration, force, weight. quantities and give examples of both.
To calculate the average speed of an object using two different equations.
To perform the prescribed practical to calculate the average speed of an object down a ramp.
What are scalars? (Higher tier only)
A scalarA physical quantity that has magnitude (size) only. A scalar quantity does not have a direction. Examples: distance, speed, mass, time, energy, temperature. quantity is something that can be measured but only has a size (magnitude).
A scalar quantity does not have a direction.
Distance is an example of a scalar quantity:
Distance is the total number of metres moved regardless of the direction.
What types of scalar quantities are used in physics?
Some scalar quantities used in physics are:
mass, e.g. mass = 80 kg
time, e.g. time = 20 s
temperature, e.g. temperature = 20oC
area, e.g. area = 200cm2
density, e.g. density = 1.0 g/cm3
speed, e.g. speed = 5 m/s
rate of change of speed, e.g. rate of change of speed = 6 m/s2
What are vectors? (Higher tier only)
A vectorA physical quantity that has magnitude (size) and direction. Examples: displacement, velocity, acceleration, force, weight. quantity is something that can be measured but the direction is important.
displacementA distance measured in a specified direction. is an example of a vector quantity as it has both size and direction:
What type of vector quantities are used in physics?
To show the direction of a vector on a diagram, an arrow is used.
The direction of movement shows the difference between a scalar and vector quantity.
Some vector quantities used in physics are:
force, e.g. force = 20 N (to the left)
displacement, e.g. displacement = 50 km (right)
acceleration, e.g. acceleration = 9.8 m/s2 (downwards)
weight, e.g. weight = 10 N (downwards)
velocity, e.g. velocity = 20 m/s (upwards)
What is speed?
Speed is a measure of how fast something is travelling.
It is the distance travelled in 1 second (or in 1 hour).
d = distance (m);
s = speed (m/s);
t = time (s)
Speed is measured in m/s or km/h (or mph in UK cars).
\( \text{speed}=\frac{\text{distance~travelled}}{\text{time~taken}}\)
speedThe rate of change of distance. It is the distance travelled in one second. Measured in m/s. , or distance, or time can be calculated using the dst triangle.
Cover the letter you want to find to get the formula you need.
- d = s × t
- s = d ÷ t
- t = d ÷ s
How to calculate average speed
Sometimes the speed of an object can change during a journey.
To distinguish between the initial speed and the final speed, the letters \(u\) and \(v\) are used.
If the initial speed and the final speed of an object are known, then the average speed of the object over the journey can be calculated using the equation:
Average speed = \(\frac{\text{initial speed + final speed}}{\text{2}}\)
This can be written as: average speed = \(\frac{\text{u + v}}{\text{2}}\)
If the object is not moving, then it is said to be stopped, or stationary or at rest.
If a question states that an object is initially at rest, this means the initial speed = 0 m/s
Question
A motorbike is initially at rest, it increases its speed to 28m/s.
Find its average speed over the journey.
Answer
Initial speed = 0 m/s (at rest)
Final speed = 28 m/s
Average speed = \(\frac{\text{initial speed + final speed}}{\text{2}}\)
Average speed = (0 m/s + 28 m/s) ÷ 2 = 28m/s ÷ 2 = 14 m/s.
The average speed of the motorbike is 14 m/s.
Question
A car travelling at 30 m/s decreases its speed to 22m/s.
Find its average speed over the journey.
Answer
Initial speed = u = 30 m/s
Final speed = v = 22 m/s
Average speed = \(\frac{(u + v)}{2}\)
Average speed = (30 m/s + 22 m/s) ÷ 2 = 52m/s ÷ 2 = 26 m/s.
The average speed of the car is 26 m/s.
Question
An object is dropped from rest.
Find the speed at which it hits the ground if the average speed is 18 m/s.
Answer
Initial speed = 0 m/s (dropped from rest)
Average speed = 18 m/s
Average speed = \(\frac{(initial~speed~+~final~speed)}{2}\)
18 m/s = (0 m/s + final speed) ÷ 2
18 m/s x 2 = (0 m/s + final speed)
36 m/s = final speed
The final speed of the object is 36 m/s.
What are the two equations for calculating average speed?
Key fact
There are two equations for calculating average speed (note: these will only work during constant accelerationThe rate of change of velocity. It is measured in metres per second squared (m/s²). Acceleration = change of velocity ÷ time taken.):
\(\text{Average~speed}=\frac{\text{total~distance~travelled}}{\text{total~time~taken}}\)
\(\text{s}=\frac{\text{d}}{\text{t}}\)
\(\text{Average~speed}=\frac{\text{(initial speed~+~final speed)}}{\text{2}}\)
\(\text{Av s}=\frac{\text{(u~+~v)}}{\text{2}}\)
You decide which equation to use, depending on the quantities given in the question.
Prescribed practical P1: Motion down a ramp
A guide to carrying out an experiment to investigate the relationship between speed and height.
What is the purpose of prescribed practical P1?
Using simple apparatus investigate experimentally how the average speed of an object (e.g. a marble) moving down a ramp depends on the height of the ramp.
What are the variables involved in prescribed practical P1?
The main variables in a science experiment are the independent variable, the dependent variable and the control variables.
The independent variable is what we change or control in the experiment.
The dependent variable is what we are testing and will be measured in the experiment.
The control variables are what we keep the same during the experiment to make sure it’s a fair test.
In this experiment the:
Independent variable is the height of the ramp.
Dependent variable is the average speed of the marble. To calculate the average speed, we have to measure the time taken for the marble to travel a measured length of the ramp.
Control variables are: the distance marble travels along the ramp, the mass of the marble, the type of marble used, the surface of the ramp, the initial speed of the marble.
Remember - these variables are controlled (or kept the same) because to make it a fair test, only one variable can be changed, which in this case is the vertical height of the ramp.
What equation is used to calculate average speed?
Average speed = \(\frac{distance~travelled}{time~taken}\)
What is the prediction?
As the height of the ramp increases, the average speed of the marble will also increase.
What is the justification for the prediction?
As the height of the ramp increases, the gravitational potential energyThe energy an object possesses due to its position above the ground. of the marble will also increase.
As the marble moves down the runway, its gravitational potential energy is converted to kinetic energyThe energy an object possesses by being in motion..
From the conservation of energy, the greater the amount of gravitational potential energy at the top, the greater the amount of kinetic energy at the bottom.
If the marble has a greater amount of kinetic energy at the bottom of the ramp, it will have greater speed.
This justifies the prediction that, average speed will increase as the vertical height of the ramp increases.
What apparatus is used in prescribed practical P1?
Large marble, adjustable support, ramp, marker pen, metre rule, 50 cm rule, stop clock, safety goggles.
Method
- Set up the apparatus as shown in the diagram
- With the marker pen mark a starting line, A, near the top of the ramp
- Likewise, mark a finishing line, B, near the bottom of the ramp
- Measure the distance between A and B with a meter rule. Record this distance in metres in a suitable table. This distance will remain unchanged throughout the experiment
- Adjust the support so that the ramp has a vertical height at A of 5 cm. Measure the distance with a 50 cm rule and record in the table
- Place the marble at A. Release from rest and simultaneously start the stop clock
- Stop the stop clock when the marble reaches B. Record the time taken in seconds in the table
- Repeat twice more and then calculate the average time. Record in the table
- Calculate the average speed using the equation:
average speed = \(\frac{distance~travelled}{average~time~taken}\) - Repeat the procedure for a total of 6 different vertical heights, increasing the height by 5 cm each time
- Plot a graph of average speed in m/s on the y-axis against vertical height in m on the x-axis
Safety
Secure the ramp with a G-clamp in the centre of the bench, so it doesn’t fall off on to someone’s foot.
Make sure the marble doesn’t fall on to the floor and someone slips on it, a small carboard box could be placed at the end ofthe ramp to “catch” the marble.
Wear safety goggles in case a marble hits someone in the eye.
| Vertical height of ramp / cm | Distance travelled / m | Time taken / s (1) | Time taken / s (2) | Time taken / s (3) | Average time taken / s | Average speed / m/s |
|---|---|---|---|---|---|---|
| 5 | 1.75 | |||||
| 10 | 1.75 | |||||
| 15 | 1.75 | |||||
| 20 | 1.75 | |||||
| 25 | 1.75 | |||||
| 30 | 1.75 |
How to make the measurement of time more reliable
The measurement of the time taken for the marble to roll down the ramp was made more reliable by repeating the measurement for each height three times and calculating an average.
What is the main cause of inaccuracy in this experiment?
The main cause of inaccuracy in this experiment is the reaction time when the person starts and stops the stop clock.
The accuracy was improved by:
Ensuring that the time taken for the marble to roll down the ramp is as long as possible.
This can be done by:
- Making the distance between A and B as large as possible.
- Keeping the vertical height as small as possible, so that the marble doesn’t move too fast.
What is the conclusion of prescribed practical P1?
As the vertical height of the ramp increases, the average speed of the marble also increases, in line with the prediction.
However, the average speed is not directly proportional to the average speed as the line of best fit is not a straight line through the origin.
Variation of the experiment
A different way of investigating motion down a ramp would be to use a ramp of fixed height as shown below:
In this experiment the:
Independent variable is the distance the marble travels down the ramp. (20 cm, 40 cm, 60 cm, 80 cm, 100 cm).
Dependent variable is the average speed of the marble. To calculate the average speed, we have to measure the time taken for the marble to travel a measured length of the ramp.
Control variables are: the height of the ramp, the starting position of the marble, the mass of the marble, the type of marble used, the surface of the ramp, the initial speed of the marble.
How much do you know about calculating motion?
More on Unit 1: Motion
Find out more by working through a topic
- count2 of 4

- count3 of 4
- count4 of 4