Module 1 (M1) - Handling Data - Pie charts

Pie charts

Pie charts use different-sized sectors of a circle to represent data.

The of each item is represented by the size of the angle of the sector.

They should be clearly labelled, either directly on the pie chart or by means of a colour-coded key.

Constructing a pie chart from a frequency table

To produce a pie chart, data is required. The data often comes in the form of a table.
To create a pie chart, the size of the angles needed must be calculated.
1. Add the total frequency in the table.
2. Divide 360° by the total frequency.
3. Multiply each frequency by this value. These are the angles for each sector.
4. Construct a circle and draw a vertical line from the top to the centre.
5. In a clockwise direction, use a protractor to plot each angle in turn.
6. Label each sector or use a key to colour code each.
7. Give your pie chart a title.

Skip image gallery

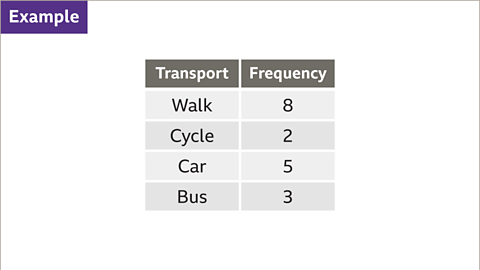
Image caption,
A student asked their friends how they got to school. The table shows the results. Construct a pie chart to represent the data.
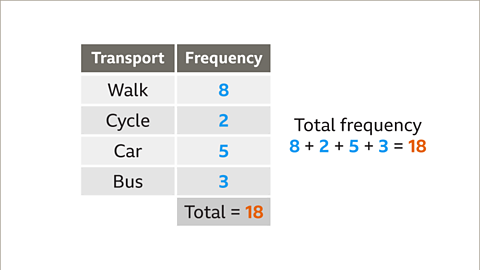
Image caption,
To construct a pie chart the angles needed must be calculated. First, add the frequencies. In this table the frequencies total 18
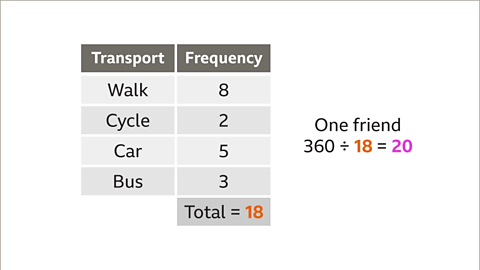
Image caption,
Divide 360° by this value. 360 ÷ 18 = 20°. This means each friend is equivalent to 20° in the pie chart.
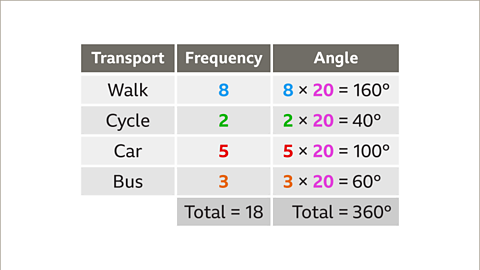
Image caption,
Multiply each frequency by 20 to calculate the angles required. Walk = 8 × 20 = 160. Cycle = 2 × 20 = 40. Car = 5 × 20 = 100. Bus = 3 × 20 = 60. These angles should add up to 360°. If they do not add up to 360°, something is incorrect.
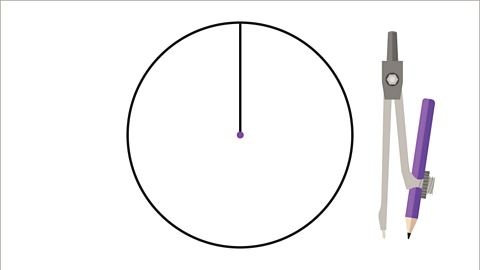
Image caption,
To plot the pie chart, start by constructing a circle. Use a pair of compasses. Add a vertical line from the centre to the top of the circumference.
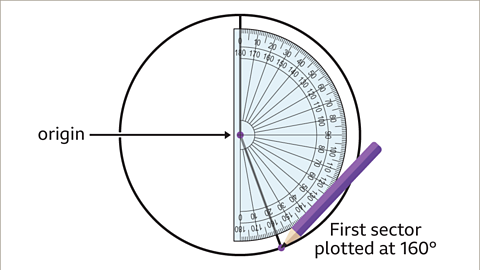
Image caption,
The first sector to be drawn is to represent the friends who walk to school. This angle needs to be drawn at 160°. Position the protractor on top of the circle so that the origin is on the circle’s centre and the zero on the outer degree scale is aligned with the vertical line. Mark the angle at 160°. Remove the protractor and draw a straight line from the centre passing through this point.
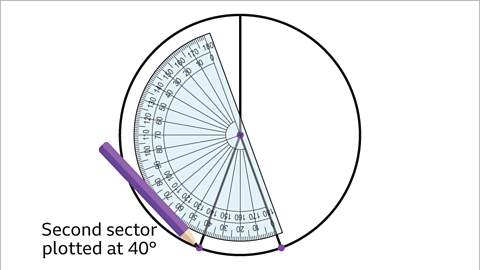
Image caption,
The second sector to be drawn is to represent the friends who cycle to school. This angle needs to be drawn at 40°. Rotate the protractor, keeping the origin on the centre of the circle, and with the zero on the outer degree scale now aligned with the previous line. Mark the angle at 40°. Remove the protractor and draw a straight line from the centre passing through this point.
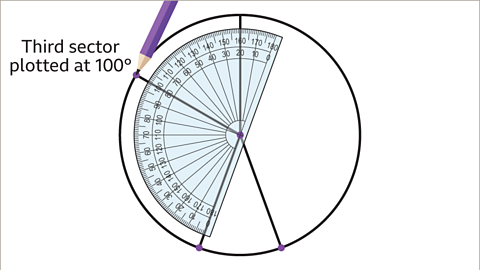
Image caption,
The same image of the partially constructed pie chart as the previous. The protractor has been rotated such that the origin of the protractor remains on the central dot and the line plotted at one hundred and sixty degrees is aligned to the zero on the outer scale of the protractor. A line has been plotted from the centre at an angle of forty degrees. Written left: Second sector plotted at forty degrees. A pencil has been drawn at the end of the plotted line.
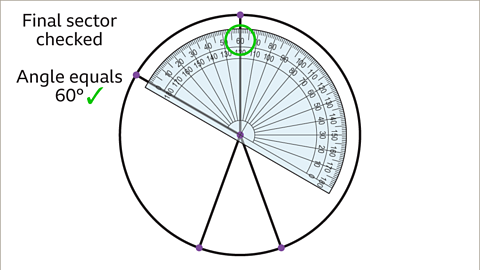
Image caption,
The third sector to be drawn is to represent the friends who use a car to travel to school. This angle needs to be drawn at 100°. Again, rotate the protractor , keeping the origin on the centre of the circle and aligning the zero on the outer degree scale with the previous line. Mark the angle at 100°. Remove the protractor and draw a straight line from the centre passing through this point.
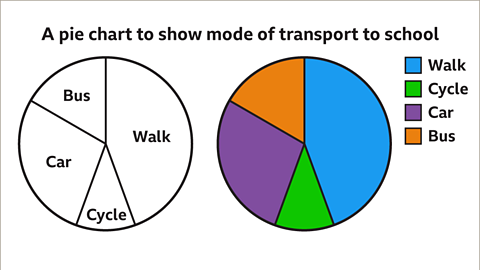
Image caption,
All that is left to do is to label the pie chart and give it a title. Each sector can be labelled, or it can be colour coded with a key. An appropriate title for this example would be ‘A pie chart to show mode of transport to school’.

Interpreting pie charts

The frequency of each item is represented by the angle of each sector in a pie chart.

To calculate the frequency for a sector:

Measure the angle for the sector using a protractor;
Write the angle as a fraction of the full circle, 360°
Multiply by the total frequency.

Example

This pie chart shows the outcomes of 24 rugby fixtures.

It is clear to see that the team won most of their matches as win is the largest sector and it is more than half.

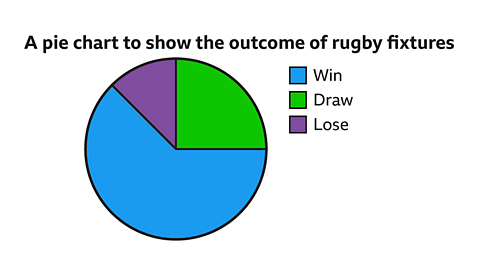
Using fractions and angles to interpret a pie chart. An image of a pie chart. The pie chart is split into three sectors. The sectors have been coloured, in a clockwise direction, green, blue, and purple. The green sector has an angle of ninety degrees, the blue sector has an angle of two hundred and twenty five degrees, and the purple sector has an angle of forty five degrees. Written right: a key, blue equals win, green equals draw, and purple equals lose. Written above the pie chart: A pie chart to show the outcome of rugby fixtures.

#### How many games did the team draw?

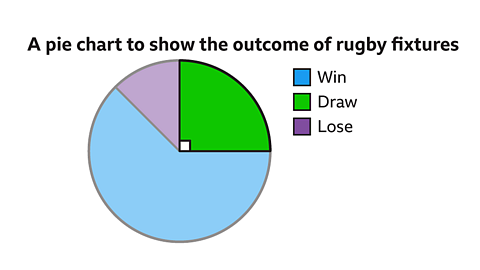
The same image of the pie chart as the previous. The green sector, for draw, has been highlighted. The angle of the sector has been marked with a right angle symbol. The quarter is coloured green.

Answer:
A Draw is the green sector.

Measure the angle for the sector using a protractor;
The angle for draw is 90°
Write the angle as a fraction of the full circle, 360°
\(\frac{90}{360}=\frac{1}{4}\)
Multiply by the total frequency.
\(\frac{1}{4}=\times 24 = 6\)

The team had 6 draws.

#### How many games did the team win?

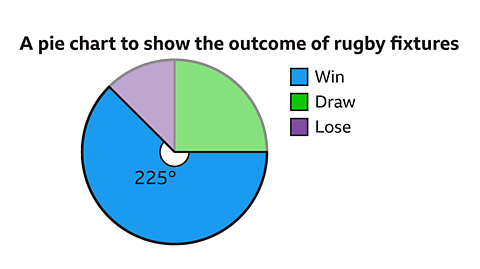
Measure the angle for the sector using a protractor;
The angle for draw is 225°
Write the angle as a fraction of the full circle, 360°
\(\frac{225}{360}\)
Multiply by the total frequency.
\(\frac{225}{360}\times 24 = 15\)

The team won 15 games.

A pie chart may have percentages to show what each part represents.

To calculate the frequency from a percentage:

Write the percentage as a fraction of 100.
Multiply by the total frequency.

Example

This pie chart shows the favourite hobbies of 660 pupils.

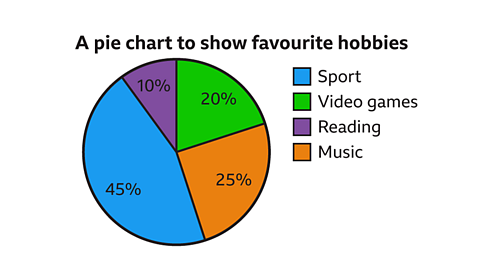
Using percentages to interpret a pie chart. An image of a pie chart. The pie chart is split into four sectors. The sectors have been coloured and a percentage has been written in each. In a clockwise direction these are: green, twenty percent, orange, twenty five percent, blue, forty five percent, and purple, ten percent. The angles of the sectors are proportionate to the percentage. Written right: a key, blue equals sport, green equals video games, purple equals reading, and orange equals music. Written above the pie chart: A pie chart to show favourite hobbies.

How many pupils said sport was their favourite hobby?

To calculate the frequency from a percentage:

Write the percentage as a fraction of 100.
\(\frac{45}{100}\)
Multiply by the total frequency.
\(\frac{45}{100} \times 660 = 297\)

Sport was chosen by 297 pupils.

Question

The pie chart shows the types of pizza sold during one evening at Milo’s Pizza Van.

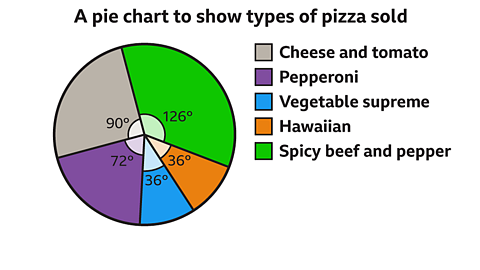
An image of a pie chart showing the types of pizza sold from Milo's pizza van. There are 5 sections of the pie chart, with their angles labelled. The green section is labeled 126 degrees. The orange section is labelled 36 degrees. The blue section is labelled 36 degrees. The magenta section is labelled 72 degrees. The grey section is labelled 90 degrees. A colour-key to the right of the pie chart shows the types of pizza sold. Grey is cheese and tomato. Magenta is pepperoni. Blue is vegetable supreme. Orange is Hawaiian. Green is spicy beef and pepper.

How many of the 240 pizzas sold were spicy beef & pepper?

Module 1 (M1) - Handling data - Pie charts

Pie charts

Constructing a pie chart from a frequency table

Interpreting pie charts

Example

Example

How many pupils said sport was their favourite hobby?

Question

Answer:

Test yourself

More on M1: Handling data

Pie charts

Constructing a pie chart from a frequency table

Interpreting pie charts

Example

Example

How many pupils said sport was their favourite hobby?

Question

Show moreShow less

Answer:

Test yourself

More on M1: Handling data