Frequency diagrams and frequency polygons - KS3 Maths

Key points

An image of a frequency diagram. — Image caption,
A frequency diagram is a type of graph used to represent a continuous set of grouped data.

A frequency diagram is a type of graph used to represent a set of grouped data.
This may be a set of data with many individual values. Only by grouping the data and producing a graph can meaningful analysis be achieved. Eg the amount of rainfall each day over a year.
A frequency diagram is similar to a bar chart in appearance as it uses different height bars to represent the of each range. However, there are no gaps between the bars.
In a frequency diagram the frequency is represented on the . The labelling on the is a continuous number scale.
A frequency polygon is similar to a frequency diagram but uses connected lines to represent the frequencies rather than bars.

Drawing and interpreting frequency diagrams and polygons

To produce a frequency diagram data is required. The data often comes in the form of a table.

To create a frequency diagram:

Look for the largest frequency in the table.
Draw a vertical axis on square paper or graph paper.
Choose an appropriate scale for this axis and label the axis up to the largest frequency. For example increments of one, two, five and ten may be appropriate.
Look at the range of data for the horizontal axis. Choose an appropriate scale for this axis. A may be required.
Draw and label the horizontal axis.
Draw each bar the correct height, based on the frequencies, and between the
Check each axis is labelled correctly and then give the frequency diagram a title.

Examples

Skip image gallery

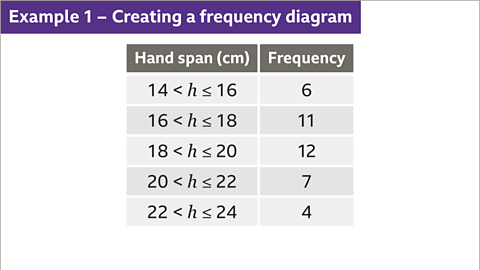
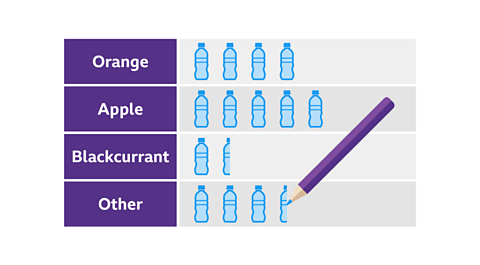
Image caption,
A student recorded the length of 40 pupils’ hand spans. Construct a frequency diagram based on the data.
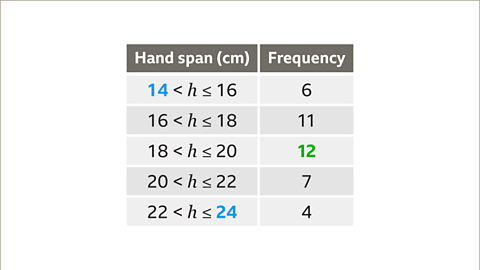
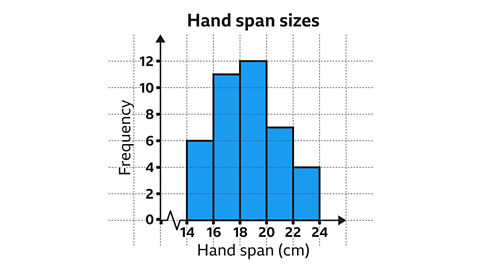
Image caption,
First, identify the largest frequency. The largest frequency is 12. Therefore, the scale on the vertical axis must go up to at least 12. The smallest and largest value for the horizontal scale are 14 and 24 centimetres. The horizontal axis will need to include this range.
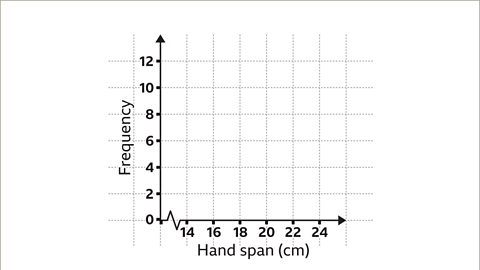
Image caption,
Now draw the vertical axis and number it in regular intervals. In this example, the scale is increasing in increments of two. Label the axis as ‘Frequency’. Draw the horizontal axis and number it in regular intervals. In this example, the scale is increasing in increments of two. A false origin has also been used. Label the axis appropriately. In this example, the label is ‘Hand span’.
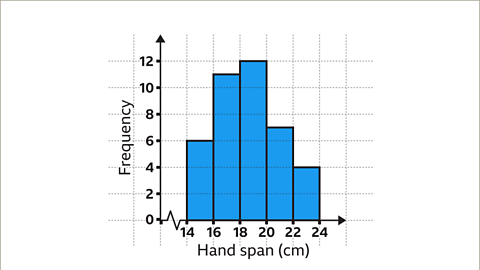
Image caption,
Draw each bar the correct height based on the frequency. For example, the bar for 16 < h ≤ 18 has a frequency of 11. Since the vertical scale is increasing in increments of two, it requires the height of the bars showing odd numbers to be exactly between the even numbers along the vertical axis.
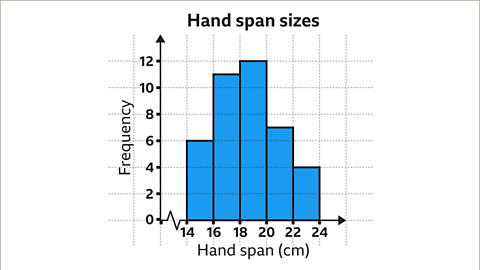
Image caption,
Finally, give the graph an appropriate title.
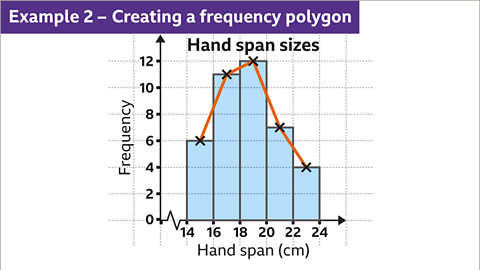
Image caption,
A frequency polygon can be created for the same set of data. Instead of drawing bars, plot the midpoint of the class interval and the frequency. These points are joined by line segments.
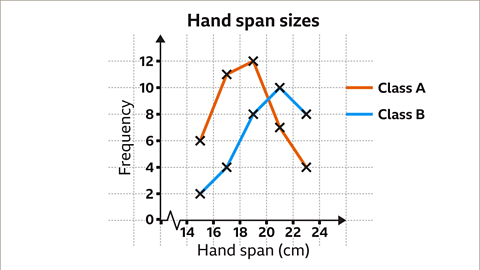
Image caption,
The advantage of using a frequency polygon is that it allows similar sets of data to be plotted on the same graph. Comparisons between the two sets can then be made. For example, this graph shows that there are three more students in Class B with a hand span in the group 20 < h ≤ 22 than in class A.
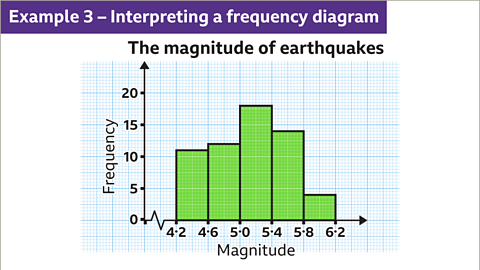
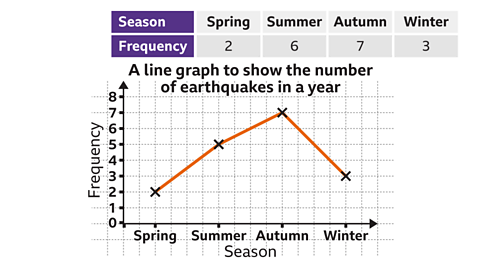
Image caption,
This frequency diagram shows the magnitude of earthquakes. The vertical scale is going up in increments of 5. Between each multiple of 5 are ten subdivisions. Each subdivision is worth 0.5
Image caption,
By looking at the frequencies of the last three bars, we can work out the number of earthquakes with a magnitude of 5.0 or larger. Earthquakes = 18 + 14 + 4 = 36. There are 36 earthquakes with a magnitude of 5.0 or larger.

Question

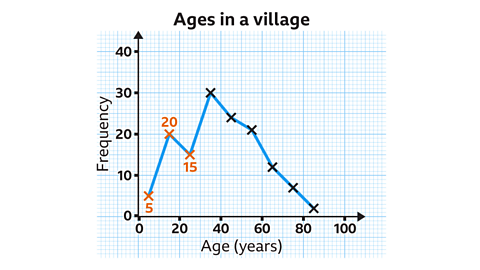
The frequency polygon shows the distribution of ages in a village. How many people living in the village are under the age of 30?

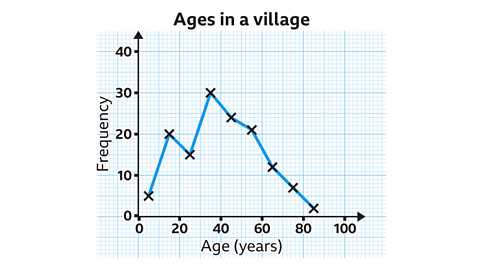
An image of a frequency polygon. A vertical axis has been drawn to the left. The axis has been labelled with numbers. The values are increasing in units of ten from zero to forty. It is subdivided into intervals of one. The axis has also been labelled, frequency. The horizontal axis has been labelled with numbers. The values are increasing in units of twenty from zero to one hundred. It is subdivided into intervals of two. The axis has also been labelled, age, measured in years. Points have been plotted at the coordinates, five, comma, five, fifteen, comma, twenty, twenty five, comma, fifteen, thirty five, comma, thirty, forty five, comma, twenty four, fifty five, comma, twenty one, sixty five, comma, twelve, seventy five comma, seven, and eighty five, comma, two. The coordinates have been joined in order by eight line segments. The line segments are coloured blue. Written above: ages in a village.

Practise using frequency diagrams and frequency polygons

Quiz

Practise understanding and using frequency diagrams and frequency polygons with this quiz. You may need a pen and paper to help you with your answers.

Real-life maths

An image of two light bulb filaments. — Image caption,
By plotting their lifespan on a frequency diagram, a manufacturer could use this information to provide a sensible estimate to how long lightbulbs will last.

Manufacturers of products employ testers and to assess new products before they go on sale to the general public.

For example, how long a lightbulb will stay working can be different from one lightbulb to the next. This may depend on tiny variations in the manufacturing process.

By testing a sample of lightbulbs, and plotting how long they last on a frequency diagram, the manufacturer can use this information to provide a sensible estimate of the lifespan of their product.