KS2

Solving problems with ratio

Part ofMathsRatioYear 6

What is ratio?

Showing the form in which ratio is written a:b.

A ratio shows how much of one thing there is compared to another.

Ratios are a way to represent proportion.

Ratios are usually written in the form a:b. For example 5:1

Showing the form in which ratio is written a:b.

Activity: How to solve problems using ratio

Complete this interactive activity to understand how to use ratio to solve problems. Then test your knowledge.

Example 1

There are 6 cupcakes in a batch - 4 chocolate cupcakes and 2 strawberry cupcakes.

The ratio of chocolate to strawberry cupcakes is 4:2.

This ratio tells us that for every four chocolate cupcakes, there are two strawberry cupcakes.

How many strawberry cupcakes will there be, if there were 24 chocolate cupcakes?

Skip image gallery

Image caption,
You know the ratio of chocolate to strawberry cupcakes is 4:2.
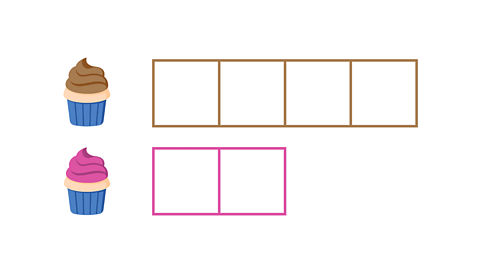
Image caption,
You can visualise a ratio using a bar model. It looks like this.
Image caption,
We can write this in a ratio table.
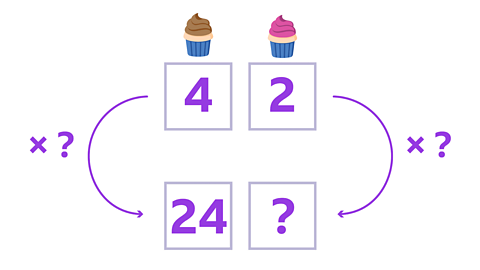
Image caption,
You need to work out how many times the number 4 (from the ratio) has been multiplied to get to 24.
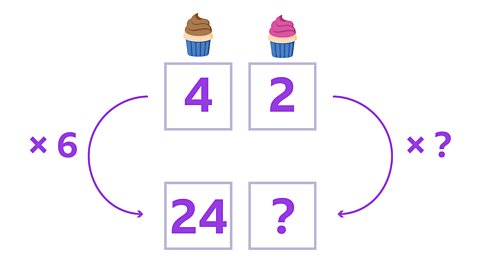
Image caption,
To find this, divide 24 by 4: 24 ÷ 4 = 6. This tells us that the ratio part for chocolate cupcakes has been multiplied by 6 to get to 24.
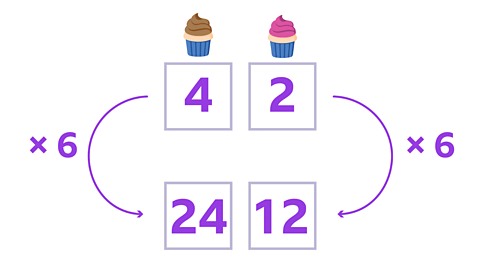
Image caption,
Since the ratio of chocolate to strawberry cupcakes is 4:2, we need to multiply the number of strawberry cupcakes in the ratio by the same number. 2 x 6 = 12.
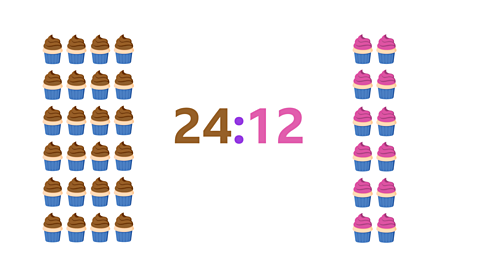
Image caption,
So, if you have 24 chocolate cupcakes, you will have 12 strawberry cupcakes.

Example 2

You have a pencil case filled with coloured pencils.

For every 3 blue pencils, you have 2 red pencils. If you have 18 blue pencils, how many red pencils do you have?

How can you scale up the ratio of blue to red pencils?

Skip image gallery

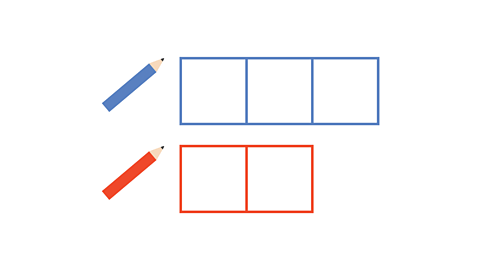
Image caption,
First, write the ratio of blue pencils to red pencils. The ratio is 3:2.
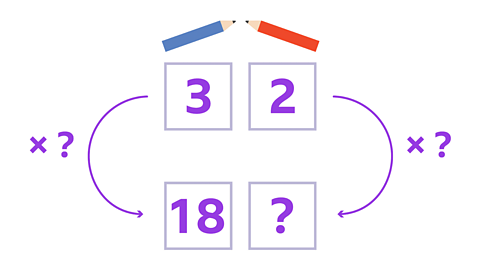
Image caption,
To scale up a ratio, you have to multiply both numbers by the same factor. You can use a ratio grid to help.
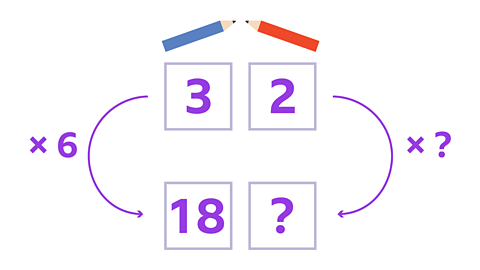
Image caption,
What number have you multiplied 3 by to get 18? 3 x 6 = 18
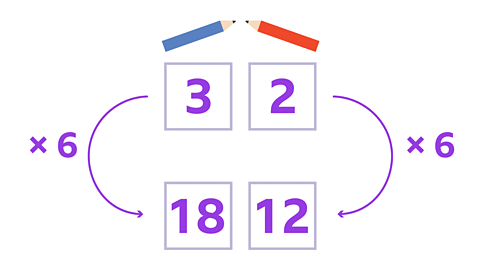
Image caption,
So you have to multiply the number of red pencils by the same number. For the red pencils: 2 × 6 = 12
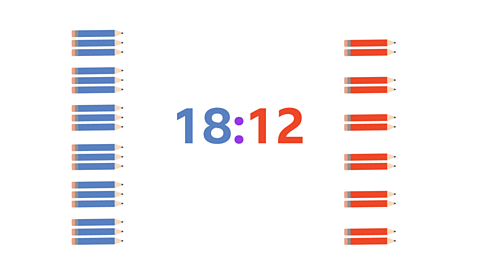
Image caption,
So, the scaled-up ratio of blue pencils to red pencils is 18:12. This means that if you have 18 blue pencils, you will have 12 red pencils.

Example 3

You are making a fruit salad. The recipe says you must follow a ratio of apples to oranges.

The ratio is 3:2.

This means for every 3 apples, you need 2 oranges.

You have 9 apples to use. How many oranges will you need to keep the same ratio?

Skip image gallery

Image caption,
First, write the ratio of apples to oranges. The ratio is 3:2. To scale up a ratio, you have to multiply both numbers by the same factor.
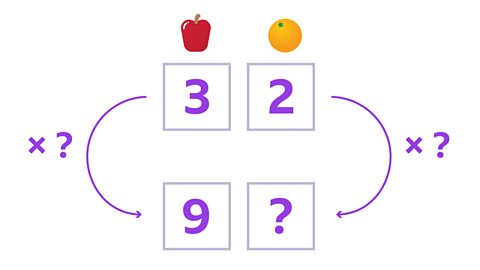
Image caption,
You can use a ratio grid to help. What number have you multiplied 3 by to get 9 apples? 3 × 3 = 9
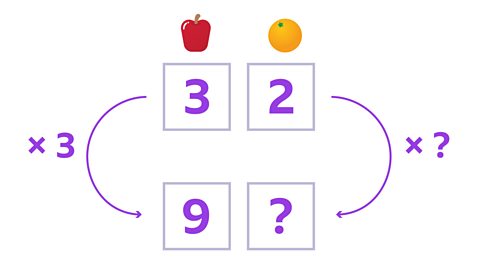
Image caption,
So, you have to multiply the number of oranges by the same number. For the oranges: 2 × 3 = 6
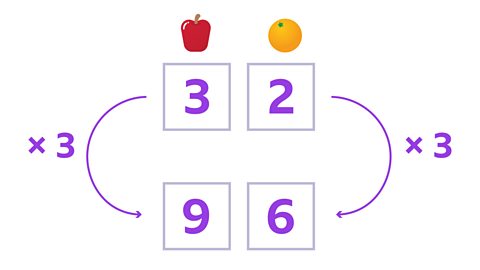
Image caption,
So, the scaled-up ratio of apples to oranges is 9:6
Image caption,
This means that if you use 9 apples, you will need 6 oranges to keep the same ratio of 3:2.

Example 4

At sports club, the coach has to order balls in sets.

Each set contains 5 footballs and 4 netballs.

The coach wants to order 5 more sets of balls.

How many footballs and netballs will the club have in total?

Skip image gallery

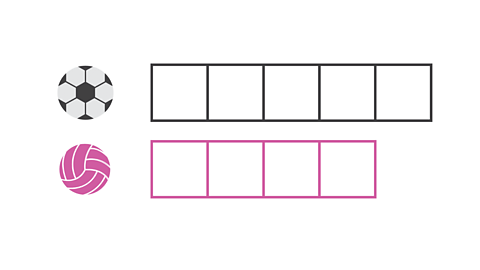
Image caption,
First, write the ratio of footballs to netballs in each set. The ratio is 5:4.
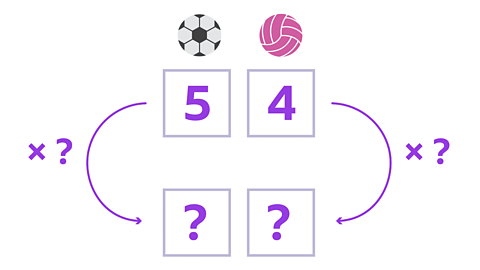
Image caption,
Next, work out the number of footballs and netballs in one set: 5 footballs 4 netballs
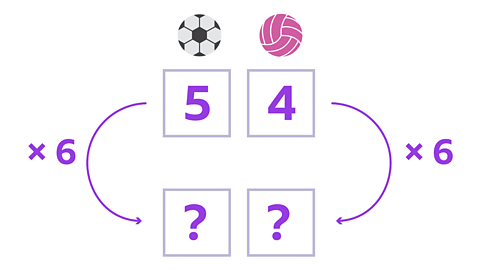
Image caption,
The coach wants to order 5 more sets. So there will be 6 sets in total. To scale up the ratio, multiply both numbers by the total number of sets. Let's use a ratio grid to help.
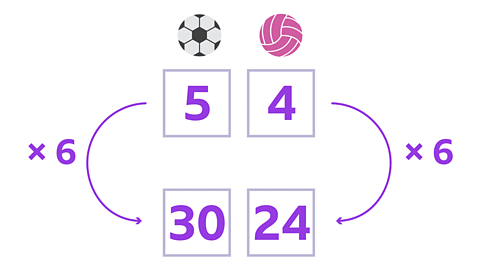
Image caption,
So, you have to multiply the number of footballs and netballs by the same number. For the footballs: 5 × 6 = 30 For the netballs: 4 × 6 = 24.
Image caption,
So, the total number of footballs and netballs will be 30 + 24, which is 54 balls.

More on Ratio

Find out more by working through a topic

Converting between ratios, fractions and percentages
count
2 of 3
Using scale factors
count
3 of 3