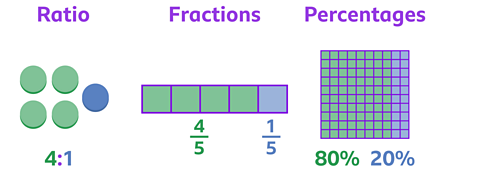
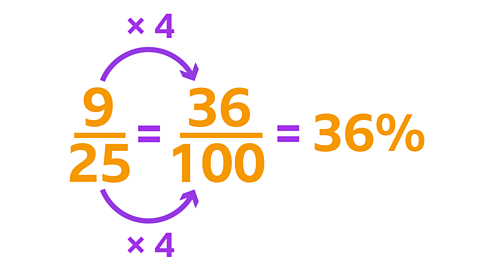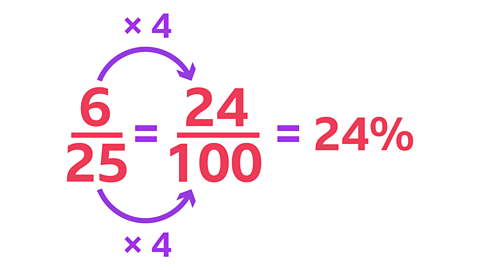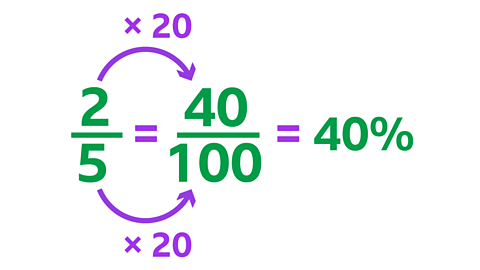Ratios, fractions and percentages
Fractions and percentages are both different ways to represent a whole.
Ratios compare two or more sizes or sets and show how they relate to each other.
There are ways of converting ratios to fractions and fractions to percentages.
Quiz: Converting between ratios, fractions and percentages
Test out your knowledge of converting between ratios, fractions and percentages with this quiz, then read on to complete the page.
How to convert between ratios and fractions
Here are some counters.
Let's describe the number of counters using a ratio and then convert that ratio to fractions.
4 counters are green and 3 counters are blue. For every 4 green counters, there are 3 blue counters.

The ratio of green counters to blue counters is 4:3.
You can also represent this ratio on a bar model.
This bar model is divided into 7 parts. There are 4 green parts and 3 blue parts.

You can now write about this using fractions, by thinking about the whole and its parts.
The bar model is split into 7 parts, which make the whole, so 7 is the denominator.
There are 4 green parts. As a fraction, it’s \(\frac {4} {7}\).
There are 3 blue parts. As a fraction, it’s \(\frac {3} {7}\).
Now, let's find out how to convert a fraction to a ratio.
Here is a bowl containing apples and oranges.
You can see that\(\frac {3} {5}\) of the items in the basket are oranges.

Putting what you know into a bar model can help you convert the information into a ratio.
If \(\frac {3} {5}\) are oranges, then \(\frac {2} {5}\) must be apples.
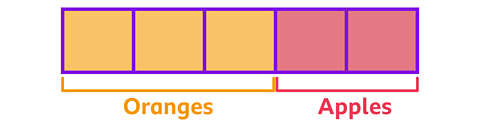
So, for every 3 oranges, there are 2 apples. The ratio of oranges to apples is 3:2.
How to convert between fractions and percentages
When converting fractions to percentages it's important to remember that per cent means ‘parts out of 100’.
So your fraction must have a denominator of 100 before you can complete the conversion.
Here are two fractions with a denominator of 100 and their equivalent percentages:
- \(\frac {25} {100}\) = 25%
- \(\frac {33} {100}\) =30%
Notice how when the denominator is 100, the numerator becomes the percentage.
Let's look at a fraction where the denominator is not 100.
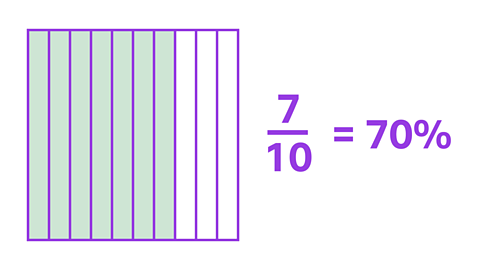
Here, a square has been split into 10 equal-sized rectangles. It is split into tenths. \(\frac {7} {10}\) of the square is shaded.
By using your knowledge of tenths and hundredths, you can say that 7 tenths is the same as 70 hundredths.
You can say that \(\frac {7} {10}\) is equivalent to \(\frac {70} {100}\).
As the denominator is now 100 you can use this to say that 70% of the square is shaded.
Tenths are easier to convert into percentages, but what about the fraction \(\frac {2} {5}\)?
To convert it, first you need to find an equivalent fraction with a denominator of 100.
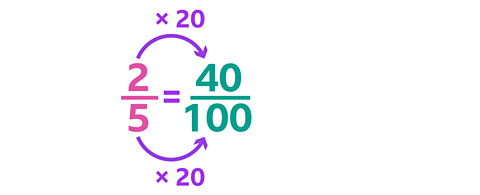
\(\frac {2} {5}\) is equivalent to \(\frac {40} {100}\), which is 40%.
You can convert percentages to fractions very simply.
Remember - per cent means ‘parts out of 100’.
Place the percentage figure as the numerator and use 100 as the denominator.
75% is equivalent to \(\frac {75} {100}\).
Then you just simply the fraction.
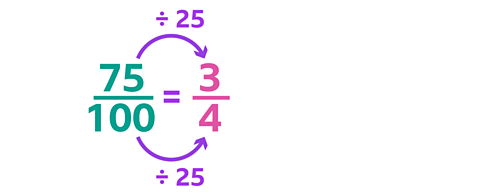
You can divide by 25 to find the equivalent fraction is \(\frac {3} {4}\).
75% = \(\frac {3} {4}\).
How to convert between ratios and percentages
To convert between ratios and percentages, first, you have to convert the ratio to a fraction.
This bar model shows a ratio of 3 blue squares to 2 pink squares.
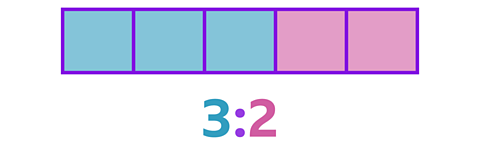
As fractions:
\(\frac {3} {5}\) are blue
\(\frac {2} {5}\) are pink
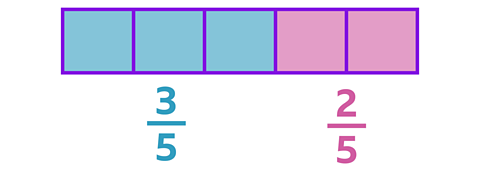
Remember, to convert to percentages, the denominator needs to be 100.
The denominator and the numerator both need to be multiplied by 20.
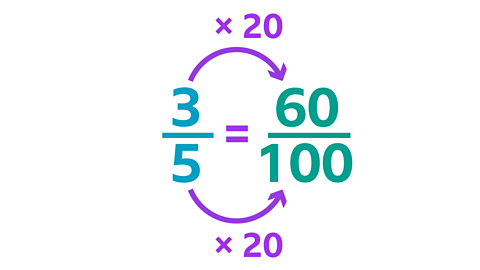
Image caption, For the blue percentage: multiply the denominator and numerator by 20, so that the denominator is 100.

Image caption, Use the numerator as your percentage. 60% of the model is blue.
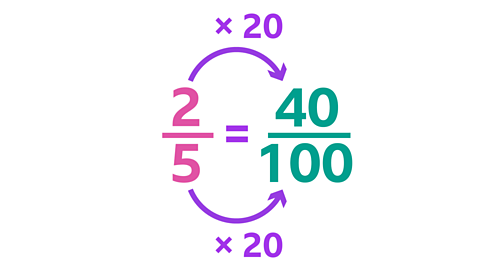
Image caption, For the pink percentage: multiply the denominator and numerator by 20 so that the denominator is 100.

Image caption, Use the numerator as your percentage. 40% of the model is pink.
1 of 4
60% of the model is blue and 40% is pink.
The percentages should add up to 100%.
60% + 40% = 100%
Example 1
Can you convert a ratio into a fraction?

If the ratio of dogs to cats to rabbits is in 3:5:2.
What fraction of animals are dogs?
What fraction are cats?
What fraction are rabbits?
Remember to simplify fractions if you can.
✓\(\frac {3} {10}\) are dogs, \(\frac {1} {2}\) are cats, \(\frac {1} {5}\) are rabbits.
To work this out, look at what the problem tells you about the original ratio before converting it into fractions.
There are 10 animals in total. 3 are dogs, 5 are cats and 2 are rabbits.
The denominator for each fraction is the total number of animals and each numerator is the total number of a particular type of animal.
So you know:
- \(\frac {3} {10}\) are dogs
- \(\frac {5} {10}\) are cats
- \(\frac {2} {10}\) are rabbits
You can then simplify some of these fractions:
- \(\frac {5} {10}\) is equivalent to \(\frac {1} {2}\)
- \(\frac {2} {10}\) is equivalent to \(\frac {1} {5}\)

Example 2
Can you convert fractions into percentages?

In this bowl of fruit, \(\frac {9} {25}\) are oranges, \(\frac {6} {25}\) are apples and \(\frac {2} {5}\) are bananas.
Convert the three fractions into percentages.
✓ To convert these fractions into percentages, remember that 100 has to be the denominator.
\(\frac {9} {25}\) and \(\frac {6} {25}\) both have 25 as the denominator, so you multiply the numerator and denominator in these fractions by 4.
For \(\frac {2} {5}\), you need to multiply the numerator and denominator by 20
1 of 3
- 36% of the fruits are oranges
- 24% of the fruits are apples
- 40% of the fruits are bananas
Check the total:
36% + 24% + 40% = 100%
Play our fun maths game Guardians: Defenders of Mathematica. gamePlay our fun maths game Guardians: Defenders of Mathematica
Use your times tables and more maths skills to defeat monsters and reclaim the Kingdom of Mathematica

More on Ratio
Find out more by working through a topic
- count3 of 3

- count1 of 3