Question
a) What fraction of the large shape is the small one?
b) What fraction of the small shape is the large one?
Answer
a) The small shape is \(\frac{3}{10}\) of the large shape.
b) The large shape is \(\frac{10}{3}\) or \({3}\frac{1}{3}\) of the small shape.
Key fact
If you are expressing a number as a fraction of a second number, the first number goes on the top and the second number on the bottom.
Question
What fraction of \({1}\) metre is \({42}~cm\)?
Give your answer in its simplest form
Answer
\({42}~cm\) as a fraction of \({100}~cm\) is:
\(\frac{42}{100}=\frac{21}{50}\)
What is a fraction?
Fractions can be illustrated by dividing a shape into equal parts, and shading a certain number of these parts.
The bottom number is the number of equal parts that diagram has been cut into, and the top number is the number of equal parts that has been shaded.
The name given to the number on the top of a fraction is the numerator, and the name given to the number on the bottom of a fraction is the denominator.
If you cut a cake into two equal pieces and eat one of them, you have eaten \(\frac{1}{2}\) (half) a cake.
If a cake is cut into five equal pieces and you eat three of them, you have eaten \(\frac{3}{5}\) (three fifths) of a cake.
\(\frac{1}{2}\) and \(\frac{3}{5}\) are examples of fractions - parts of a whole.
Equivalent fractions
Cutting the cake into six equal pieces and eating two is equivalent to cutting the cake into three equal pieces and eating one. You eat the same amount of cake in both cases.
Question
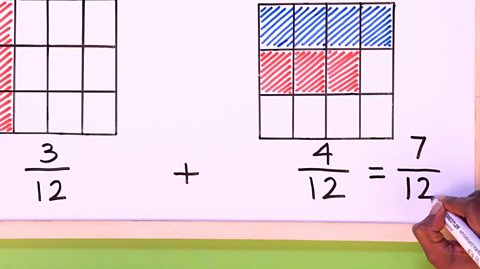
If the cake is cut into \(12\) equal pieces, how many will we have to eat in order to have the equivalent of \(\frac{1}{3}\) of the cake?
Answer
Did you get \({4}\)?
\(\frac{4}{12} = \frac{2}{6} = \frac{1}{3}\)
\(\frac{4}{12}\), \(\frac{2}{6}\) and \(\frac{1}{3}\) are all equivalent fractions.
\(\frac{1}{3}\) is equivalent to \(\frac{2}{6}\) because the top and bottom numbers have been multiplied by \(2\).
\(\frac{4}{12}\) is equivalent to \(\frac{1}{3}\) because the top and bottom numbers have been divided by \(4\).
When writing equivalent fractions, do the same multiplication or division to the top and bottom numbers.
For example, if you multiply the top by 2, you must also multiply the bottom by 2.
Simplest form
You know that: \(\frac{4}{12} = \frac{2}{6} = \frac{1}{3}\)
\({4}\) and \({12}\) have a common factor, namely \({4}\), so \(\frac{4}{12}\) can be written as \(\frac{1}{3}\) (divide the top and the bottom by \(4\)).
\({2}\) and \({6}\) have a common factor, namely \({2}\), so \(\frac{2}{6}\) can be written as \(\frac{1}{3}\) (divide the top and the bottom by \({2}\)).
However, \({1}\) and \({3}\) have no common factors, so \(\frac{1}{3}\) cannot be simplified.
When a fraction cannot be simplified we say that it is its simplest form.
A one-minute video showing how to simplify fractions.
Simplify fractions

Image caption, Click to see a step-by-step slideshow.

Image caption, WHAT YOU NEED: ruler, whiteboard, black pen, coloured pens.

Image caption, STEP 1: Write the question and circle the key information. Draw a bar and split it into 12 equal segments: the denominator of the fraction. Label the end '/12'. Shade in 9 segments and label the end of these '9': the numerator of the fraction.
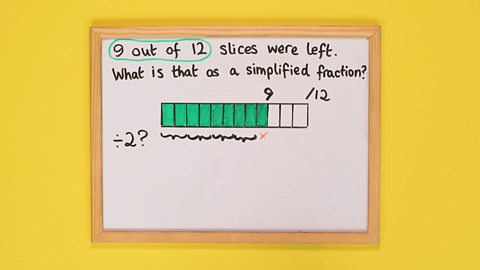
Image caption, STEP 2: Time to simplify the fraction. Look for a number that goes into both the numerator and the denominator. Start with 2. See if you can split the 9 shaded segments of the bar into 2s. This won’t work because 9 doesn’t divide by 2 exactly...

Image caption, ...so next try more numbers: 3, 5, 7 and so on. Here 3 works because 9 divides by 3, and 12 also divides by 3 exactly. You have found a common factor!
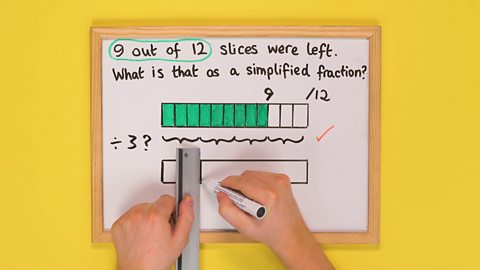
Image caption, STEP 3: Draw a bar directly below the top bar. Use the ruler to split the bar into one segment for each 3 on the top bar, and shade in the segments below the shaded segments on the top bar. You can see visually that the fraction is the same.
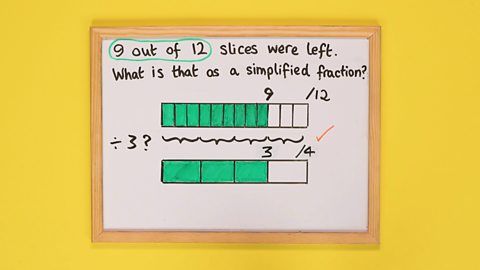
Image caption, STEP 4: Label the bottom bar with the total and shaded number of segments, here '3' and '/4'.
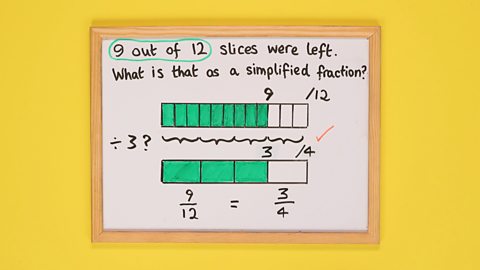
Image caption, When you write out the fractions shown on each bar you can see that 9/12 = 3/4. You have simplified 9/12 to 3/4! Can you simplify this fraction even more? If not, congratulations, you have found the simplest form of the fraction!
1 of 8
Simplify the fraction
Mixed numbers and improper fractions
Mixed numbers and improper fractions
Whole numbers
A whole number can be written as \(\frac{2}{2}\), \(\frac{3}{3}\), \(\frac{4}{4}\), etc.
Mixed numbers
\(1\frac{2}{3}\) is known as a mixed number, because it is made up of a whole number and a fraction.
So \(1 \frac{2}{3}\) can be written as:
\(\frac{3}{3} + \frac{2}{3} = \frac{5}{3}\)
Improper fractions
\(\frac{5}{3}\) is called an improper fraction, because the top number is bigger than the bottom number.
Converting from a mixed number to an improper fraction
You can write the whole number part as a fraction, with the same denominator as the other fraction, and then add the fractions together.
Example
\(1 \frac{2}{3} = \frac{3}{3} + \frac{2}{3} = \frac{5}{3}\)
Here is another example:
\(2 \frac{1}{4} = 1 + 1 + \frac{1}{4} = \frac{4}{4} + \frac{4}{4} + \frac{1}{4} = \frac{9}{4}\)
Another way to work out how many quarters there are in \(2\) wholes is to multiply the whole number, \(2\), by the denominator, \(4\).
This gives \(8\) quarters.
Add one quarter to give the improper fraction \(\frac{9}{4}\).
Converting from improper fractions to mixed numbers
You can separate the fraction into as many whole numbers as possible, with a smaller remaining fraction.
Example
\(\frac{17}{5}= \frac{5}{5} + \frac{5}{5} + \frac{5}{5} + \frac{2}{5} = 3 \frac{2}{5}\)
Another way to convert an improper fraction is to find how many whole numbers you get, by using a division.
For example let's convert \(\frac{17}{5}\) to a mixed number again.
We start by dividing the top number by the bottom number.
\({17}\) divided by \({5}\) is \({3}\) remainder \({2}\).
So the whole number part is \({3}\), and the remainder \({2}\) means there are \(\frac{2}{5}\) left over.
So the answer is \(\frac{17}{5} = 3 \frac{2}{5}\)
Question
Write \(\frac{20}{7}\) as a mixed number.
Answer
Method 1:
\(\frac{20}{7} = \frac{7}{7} + \frac{7}{7} + \frac{6}{7} = {2}\frac{6}{7}\)
Method 2:
\(\frac{20}{7} = 20 \div 7 = 2\) remainder \({6}\), so:
\(\frac{20}{7} = 2 \frac{6}{7}\)
Using a calculator
If your calculator has a fraction button you can use this to convert from improper fractions to mixed numbers.
Type in the improper fraction, press '\({=}\)', and the calculator will convert it to a mixed number.
Writing a number as a fraction of another
If you get \({7}\) out of \({10}\) in a test, you can write your score as \(\frac{7}{10}\).
\({7}\) expressed as a fraction of \({10}\) is \(\frac{7}{10}\).
Similarly, if there are \({20}\) socks in a drawer and \({4}\) of them are blue, \(\frac{4}{20}\) of the socks are blue.
\({4}\) expressed as a fraction of \({20}\) is \(\frac{4}{20}\).
We can put this into its simplest form by dividing the top and bottom numbers by \({4}\), so we get \(\frac{1}{5}\).
Ordering fractions
Which fraction is bigger: \(\frac{3}{4}\) or \(\frac{5}{7}\)?
It is hard to answer this question just by looking at the fractions.
However, if you write the fractions with the same bottom number, or denominator, the question will be easy.
\(\frac{3}{4}\) has a denominator of \(4\), and \(\frac{5}{7}\) has a denominator of \({7}\).
\({4}\) and \({7}\) both divide into \({28}\), so rewrite the fractions with a denominator of \({28}\).
\(\frac{3}{4}= \frac{21}{28}\)
\(\frac{5}{7}= \frac{20}{28}\)
It is easy to see that \(\frac{21}{28}\) is bigger than \(\frac{20}{28}\).
Therefore \(\frac{3}{4}\) is bigger than \(\frac{5}{7}\).
To compare fractions, first write them with the same bottom number, or denominator.
Test section
Question 1
Which fraction is equivalent to \(\frac{1}{3}\):
\(\frac{3}{10}\), \(\frac{5}{15}\) or \(\frac{10}{13}\)?
Answer
Fractions are equivalent when the numbers on the top and bottom are multiplied by the same number.
\(\frac{{1}\times{5}}{{3}\times{5}} = \frac{5}{15}\)
Question 2
What is \(\frac{4}{20}\) in its simplest form?
Answer
Fractions are simplified by dividing the numerator and denominator by the same number.
Here, they've been divided by \({4}\).
So the correct answer is \(\frac{1}{5}\)
Question 3
What is \({1}\frac{3}{4}\) as an improper fraction?
Answer
Remember to calculate the number of quarters in \({1}\) whole, then add them to the three quarters to get a total of seven quarters or \(\frac{7}{4}\)
Question 4
What is \(\frac{15}{4}\) as a mixed number?
Answer
You need to calculate how many times \({4}\) fits into \({15}\) (\({3}\) whole = \({12}\)) with \({3}\) remaining.
So the answer is \({3}\frac{3}{4}\).
Question 5
Which is the biggest:
\(\frac{4}{9}\), \(\frac{1}{3}\) or \(\frac{4}{7}\)?
Answer
We compare fractions by creating equivalent fractions with the same denominator.
The common denominator is \({63}\).
\(\frac{4}{9} = \frac{28}{63}\), \(\frac{1}{3} = \frac{21}{63}\), \(\frac{4}{7} = \frac{36}{63}\).
Therefore, \(\frac{4}{7}\) is the biggest.
Question 6
Andy gets \({7}\) out of \({25}\) questions wrong in his maths test.
What fraction of the questions does Andy answer correctly?
Answer
To create the fraction, remember to put the number of correct answers over the total number of questions: \(\frac{18}{25}\).
More on Fractions
Find out more by working through a topic
- count2 of 8

- count3 of 8

- count5 of 8