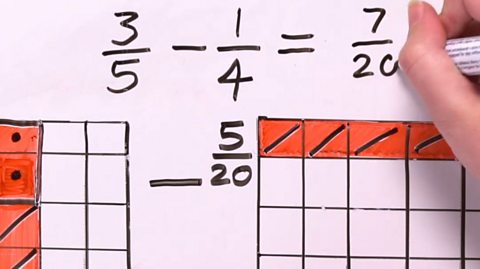Adding and subtracting fractions
If you were to add \(\frac{1}{2}\) and \(\frac{1}{3}\), it is hard to picture what the answer would be.
Rewriting the fractions with a common bottom number, or denominator (in this case, \({6}\)), makes it easier.
Remember, you can only add and subtract fractions when the bottom numbers, or denominators, are the same.
So, to add or subtract fractions:
- Change the fractions so they have the same denominator.
- Add or subtract the top numbers, or numerators.
Example
\(\frac{1}{2} + \frac{1}{3} = \frac{3}{6} + \frac{2}{6} = \frac{5}{6}\)
\(\frac{7}{10} - \frac{2}{5} = \frac{7}{10} - \frac{4}{10} = \frac{3}{10}\)
Question
What is \(\frac{1}{4} + \frac{1}{3} = \)?
Answer
\(\frac{1}{4} + \frac{1}{3}= \frac{3}{12} + \frac{4}{12} = \frac{7}{12}\)
From the diagram it is clear that the denominator remains the same, as the circles have been split into the same number of parts.
Mixed numbers
To add or subtract mixed numbers, it is usually easiest to change them to improper fractions first and then change the answer back into a mixed number (if needed).
Question
\(3 \frac{1}{3} + 4 \frac{1}{2} = \)?
Answer
\(3 \frac{1}{3} + 4 \frac{1}{2} = \frac{10}{3} + \frac{9}{2} = \frac{20}{6} + \frac{27}{6} = \frac{47}{6} = 7 \frac{5}{6}\)
Alternatively, you can add the whole numbers and then the fractions:
\(3 \frac{1}{3} + 4 \frac{1}{2} = 3 + 4 + \frac{1}{3} + \frac{1}{2} = 7 + \frac{2}{6} + \frac{3}{6} = 7 \frac{5}{6}\)
Find out how to add fractions with this short video
Have a go

Image caption, Click to see a step-by-step slideshow.

Image caption, STEP 1 - When adding fractions it can be useful to visualise it. Draw a square with 4 columns and shade in one of the columns. This represents ¹/₄

Image caption, STEP 2 - Draw a second square with 3 rows and shade in one of the rows. This represents ¹/₃

Image caption, STEP 3 - Divide the first square into 3 rows. 3 is the denominator of the second fraction.
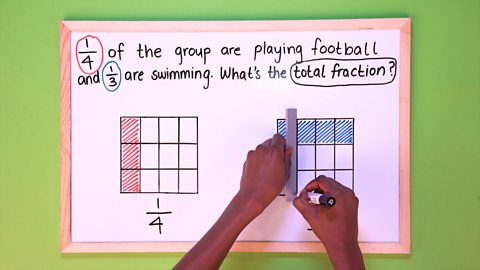
Image caption, STEP 4 - Divide the second square into 4 columns. 4 is the denominator of the first fraction.
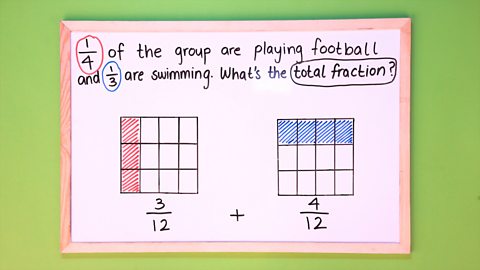
Image caption, STEP 5 - Count the coloured sections and rewrite the fractions. The first is ³/₁₂ and the second is ⁴/₁₂

Image caption, STEP 6 - Now that we have the common denominator for both fractions (12) it is simple to add them. Add 3 to 4, making 7. The answer is ⁷/₁₂
1 of 7
Find out how to subtract fractions
Have a go
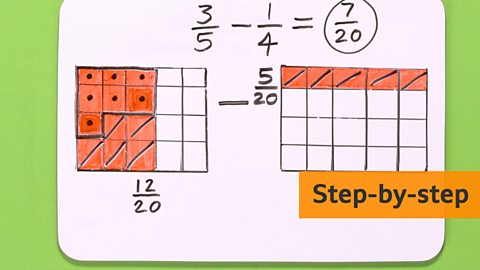
Image caption, Click here to see a step-by-step slideshow.

Image caption, WHAT YOU NEED: A whiteboard, pens, board rubber and a ruler.
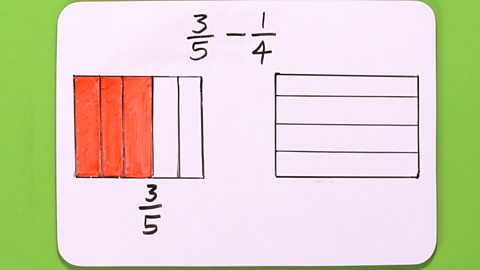
Image caption, STEP 1 - Draw a square with 5 columns (5 is the denominator of the first fraction) and a square with 4 rows (4 is the denominator of the second fraction).
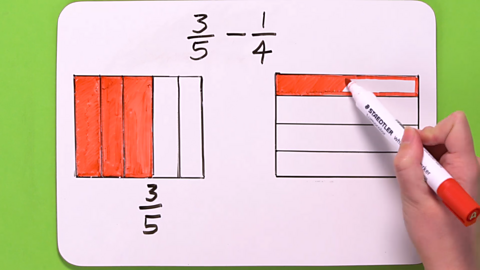
Image caption, STEP 2 - Colour 3 sections of the first square and 1 section of the second square. These represent ³/₅ and ¹/₄

Image caption, STEP 3 - Divide the first square into 4 rows (4 is the denominator of the second fraction).
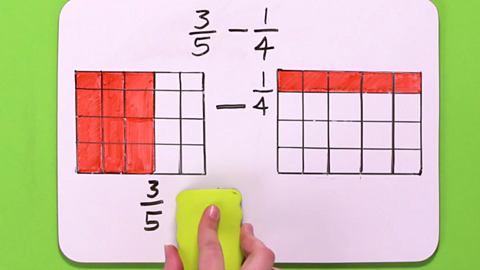
Image caption, STEP 4 - Divide the second square into 5 columns (5 is the denominator of the first fraction). Both squares now contain 20 sections. This is the common denominator.
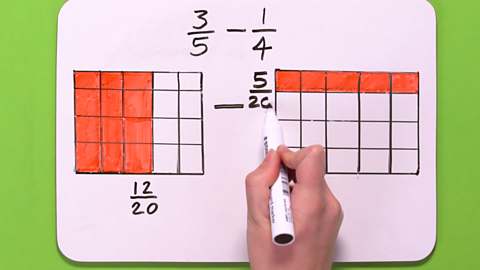
Image caption, STEP 5 - Count the coloured sections and rewrite the fractions.
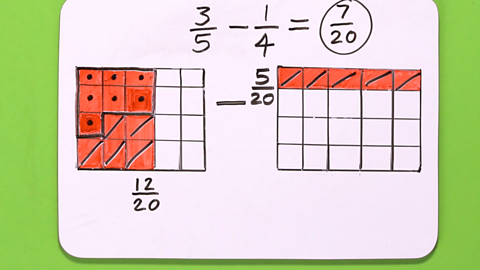
Image caption, STEP 6 - The denominator is now the same for both fractions. This is called the common denominator. Subtract 5 from 12, making 7.

Image caption, STEP 7 - The answer is ⁷/₂₀ of a mile.
1 of 9
Multiplying and dividing fractions
Multiplying fractions
\(\frac{1}{2}\) of \(\frac{1}{2} = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}\)
\(\frac{2}{3}\) of \(\frac{4}{5} = \frac{2}{3} \times \frac{4}{5} = \frac{8}{15}\)
Multiply the numerators to find the new numerator, multiply the denominators to find the new denominator, then simplify where necessary.
Question
Calculate \(\frac{3}{4} \times \frac{2}{5}\)
Answer
\(\frac{3}{4} \times \frac{2}{5} = \frac{3 \times 2}{4 \times 5} = \frac{6}{20}\)
Now put the the answer into its simplest form:
\(\frac{6}{20}= \frac{3}{10}\)
Dividing fractions
When you divide \({10}\) by \({2}\), you are working out how many \({2}\)s there are in \({10}\).
\(10 \div 2 = 5\), so there are five \({2}\)s in \({10}\).
In a similar way, when dividing \({2}\) by \(\frac{1}{2}\), you are working out how many \(\frac{1}{2}\)s there are in \({2}\).
There are four \(\frac{1}{2}\)s in \({2}\), so:
\(2 \div \frac{1}{2} = 4\)
If you divide \(1 \frac{1}{2}\) by \(\frac{1}{4}\) you are working out how many \(\frac{1}{4}\)s there are in \(1 \frac{1}{2}\).
There are six \(\frac{1}{4}\)s in \(1 \frac{1}{2}\), so:
\(1\frac{1}{2} \div \frac{1}{4} = 6\)
Do you see a pattern?
Let's write out those calculations a different way.
\(2 \div \frac{1}{2} = 4\) and \(2 \times 2 = 4\), so \(2 \div \frac{1}{2}\) is the same as \(2 \times 2\)
\(1\frac{1}{2} \div \frac{1}{4} = \frac{3}{2} \div \frac{1}{4} = 6\), so \(\frac{3}{2} \div \frac{1}{4}\) is the same as \(\frac{3}{2} \times 4 = \frac{12}{2} = 6\)
So, '\(\div\frac{1}{2}\)' is the same as ‘\(\times 2\)’.
And '\(\div\frac{1}{4}\)' is the same as ‘\(\times 4\)’.
To divide fractions, turn the second fraction upside down, then multiply.
Question
Calculate \(\frac{3}{4} \div \frac{4}{5}\)
Answer
\(\frac{3}{4} \div \frac{4}{5}= \frac{3}{4} \times \frac{5}{4} = \frac{15}{16}\)
Have a go

Image caption, Click to see a step-by-step slideshow.

Image caption, YOU WILL NEED: A whiteboard, coloured pens, paper and a pencil.

Image caption, STEP 1: Count the denominator on the first fraction, in this case it is 4. Fold the paper into that number of rows.

Image caption, STEP 2: Fold the paper into the number of columns indicated by the second denominator. 5 in this instance.

Image caption, STEP 3: Count the number of sections you have and label them as single fractions. In this example there are 20 sections, so label each one as ¹/₂₀
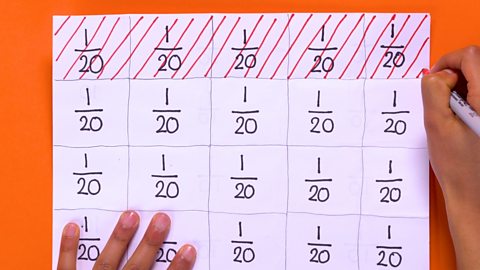
Image caption, STEP 4: Shade in the number of rows according to the numerator of the first fraction. In this example, 1 of the 4 rows are shaded.

Image caption, STEP 5: Shade in the number of columns according to the numerator of the second fraction. In this example 2 of the 5 columns are shaded.

Image caption, STEP 6: Count how many sections overlap and are shaded twice and that's your answer. In this example it is ²/₂₀

Image caption, STEP 7: Simplify the fraction if required. In this instance it is ¹/₁₀
1 of 9
Find out how to divide fractions using a bar model
How to divide by a fraction using bar modelsHow many half litre bottles can be filled with three litres of water?Draw a bar and add the number three to represent three litres of water.Divide the bar into three sectionsand add a one to each – one times three is three.You want to know about half-litre bottles, though,so draw a bar underneath one of the sections,divide it into two and write half in each block.Do the same under the remaining sections.Add together the sections in the top bar – that’s three!Divide by half.And the answer is … six!
Have a go

Image caption, Click to see a step-by-step slideshow.

Image caption, YOU WILL NEED: A whiteboard, ruler and coloured pens.

Image caption, STEP 1 - Draw a bar with a 3. In this example the number represents 3 litres of water.

Image caption, STEP 2 - Draw a bar and split it into the number you are dividing into. In this instance you are dividing 3 into equal sections. Write a 1 in each of the 3 sections.

Image caption, STEP 3 - Draw a second bar underneath one of the boxes and divide into two equal sections. Write a ½ in each section. These represent the ½ litre bottles of water and make up the number 1.

Image caption, STEP 4 - Repeat the bars under each section with a 1. Write a ½ in each section.
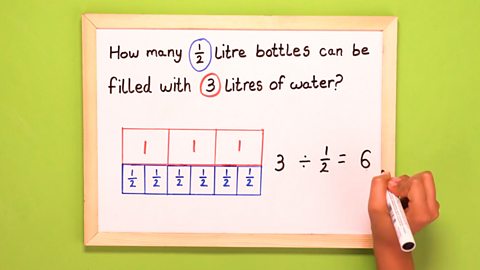
Image caption, STEP 5 - Add up how many of the smaller sections with a ½ and that's your answer! In this instance the answer is 6.
1 of 7
How do you find a fraction of a quantity?
To find a fraction of a quantity, divide by the number on the bottom of the fraction (denominator) and multiply by the number on the top (numerator).
Example
A teacher has a box containing 54 pencils and gives out \(\frac{2}{3}\) of them to his class.
How many pencils has he given out?
How many pencils are left in the box?
Divide by the (denominator) bottom number (3) to find one third.
\(54 ÷ 3 = 18\)
Now multiply by the (numerator) top number (2) to find two thirds.
\({18} \times {2} = 36\)
The teacher gives out 36 pencils.
How many pencils are left in the box?
\(54 – 36 = 18\) pencils are left.
Question
A school has 950 pupils and \(\frac{1}{5}\) of them walk to school every day.
How many pupils walk to school?
Answer
Divide by the bottom number (denominator).
\(950 ÷ 5 = 190\)
Now multiply by the top number (numerator).
\({190}\times{1} = {190}\) (no change after multiplying by 1)
190 pupils walk to school
For a unitary fraction (with 1 as the top number), just divide by the bottom number.
Question
Sophie has £64 birthday money.
She spends \(\frac{3}{8}\) of this money and saves the rest.
How much does she save?
Answer
Sophie spends \(\frac{3}{8}\) of her money so she has \(\frac{5}{8}\) left.
\(\frac{5}{8}\) of £64 \(= {~64} ÷ {8}\times{5} = {40}\)
Sophie has £40 left to save.
OR
Sophie spends \(\frac{3}{8}\) of her money.
\(\frac{3}{8}\) of £64 \(= {~64}\div{8}\times{3} = {24}\)
\(£64 - £24 = £40\)
Sophie has £40 left to save.
A one-minute video on how to work out a fraction of an amount using bar models.
How to work out a fraction of an amount

Image caption, WHAT YOU NEED: Whiteboard, pen, ruler and a calculator.

Image caption, STEP 1: Write out the problem and circle the key information. Here you want to work out one sixth of 1200 metres...

Image caption, …then draw two parallel bars. Label the top one with the length that you know in metres. The bottom bar will be split into sixths, so label the end with /6...

Image caption, …now draw vertical lines splitting the bottom bar into 6 equal parts. TIP: if it’s an even number like 6 you can start by drawing a line half way along to split the bar in two, then split the two halves into three equal parts.

Image caption, STEP 2: On the bottom bar, shade in one part, and label it with a 1. This represents 1/6 of the bar.

Image caption, STEP 3: Draw a line directly above it on the top bar and colour that part in too. Label it with a question mark. This is 1/6 of 1200 m, the amount you want to find...
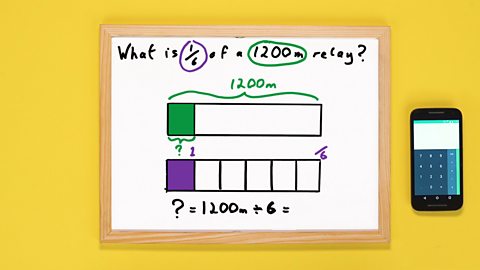
Image caption, …write your calculation down. You want to divide 1200 m into 6 parts to find how long one part is, so your calculation will be 1200 ÷ 6. Before you use a calculator, can you estimate what the answer will be?
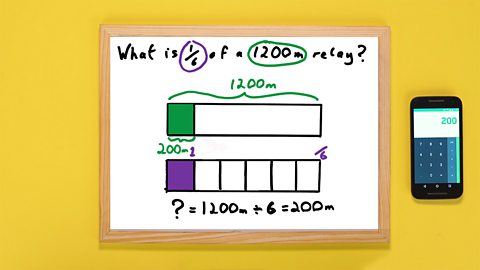
Image caption, Step 4: Use a calculator to check your estimate. Then write the answer where the question mark was. Don’t forget the right units – you can write metres or the shorter ‘m’. You’ve done it!
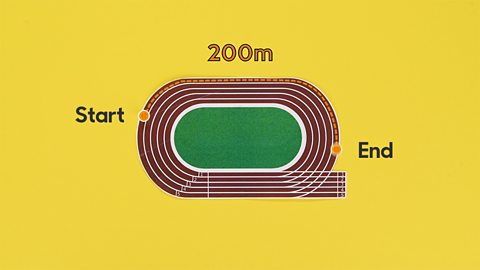
Image caption, When you’ve worked out the answer, think about what it means in context. Can you visualise it?
1 of 9
We’re going to draw a rectangle.I'm just going to mark one sixth of it.And then we're going to draw another rectangle directly underneath.And we’re just going to make a mark of where six equal squares would be.Once we’ve done this, we’re gonna draw one vertical line down,and we’re just gonna make a little note showing that this is 1200 m.Five vertical lines, so that this rectangle is split into six equal squares.And I’m going to colour in the first rectangle one colour,and then we’re going to colour the top square one colour.So we are colouring in this because it is one sixth of the entire rectangle.And then we are going to mark to show that this is one section.Because we don’t know how much one sixth is yet,we’re just going to put a little question mark.So the question mark is whatever 1200 divided by six is.200 m.So now we can show that one sixth is 200 m.I think that this method helps you understand it better,and to really learn how to do the division,I think it breaks it down more so it’s easier to understand.
Converting fractions: The great pizza party
Follow one teenager's attempt to share pizza and bills equally by using fractions and percentages. Learn how to convert fractions into decimals and percentages.
Billy Oh no. I’m starving.
(DOOR BELL)
Hey guys, the pizza’s here!
Yeah, coming, coming…
Hi there, is it all paid for?
Delivery Man Yeah, It’s already been paid online.
Billy OK. Where’s the third one?
Delivery Man There was only two in the order.
Billy Oh no. Thank you
Oh no… how on earth am I going to split this into nine?
One thing they always go on about at school is pizzas, fractions and percentages.
If I can’t work this out…
Friends Pizza, Pizza, Pizza!
Billy Coming! I’m just cutting it up now.
Right, you can do this.
I have to share two pizzas between nine people.
That’s two divided by nine. I think I’ll get my calculator for this.
Now, let’s take this nice and slowly.
Well to convert a fraction to a decimal I need to divide the numerator by the denominator.
So the fraction is two ninths. What’s two divided by nine?
Two divided by nine equals naught point two, two, two, two, two.
That’s a recurring decimal.
Now to convert a decimal to a percentage you multiply the decimal by 100.
So x 100 equals 22.222222222%
But how does that help me cut up pizzas?
Hang on, if I just stick to fractions.
I need two ninths of two pizzas.
That’s one ninth of each pizza.
Hey that’s so cool.
Nine. That’s easy. That’s divisible by three.
Cut them into thirds.
Then cut each third into three, that’s great.
Here we go guys - it’s two pieces each!
Wow that’s a disaster.
Having shown off about how good I was at fractions,
they’ve now all challenged me to work out what percentage of the bill they all have to pay.
So without Kevin the birthday boy, there’s eight of us.
That’s an 8th each and to get the decimal divide the numerator by the denominator.
That’s one divided by eight.
To go to a percentage you multiply by 100.
Let’s just work it out.
I’m so good at this.
Oh no!
Mum, I need your lipstick.
So what’s the simplest way of doing this.
So from an eighth as a fraction to a percentage is one divided by eight, times 100, the same as 100 divided by eight.
So, eight into 100. Eight goes into 10 once, with two left over so I carry that to the units.
Eight goes into 20 twice, and there’s four left over and I need to carry that to the first decimal place.
Eight into 40 is exactly five.
So I can see that an 1/8th is the same as 12.5%.
What’s 12.5% of the bill which was £28.
I can use my phone, why didn’t I think of that.
Now I don’t know what this percentage button does but I know that if I’m changing a percentage to a fraction or a decimal then I need to divide by 100.
So 12.5% is the same as 12.5 divided by 100, which is 0.125.
So that’s 0.125 multiplied by 28.
That’s £3.50.
So eight of us pays £3.50 each.
Now, where am I going to find some change!
Test section
Question 1
A laptop usually costs \(£420\) but is reduced by \(\frac{1}{3}\) in a sale.
What is the sale price?
Answer
The correct answer is \(£280\).
Question 2
For a science experiment, a 1 litre cylinder is \(\frac{7}{10}\) full of solution.
How many millilitres of solution is in the cylinder?
Answer
The correct answer is \(700 ml\).
Question 3
A year group of \(120\) pupils voted for one of \(3\) options for a school trip.
\(\frac{5}{12}\) voted for a trip to Portrush and \(\frac{1}{6}\)voted to go to the cinema.
The rest voted to go to W5.
How many pupils voted to go to Portrush?
Answer
The correct answer is \(50\) pupils went to Portrush.
Question 4
Using the information from Question 3, how many pupils voted to go to W5?
Answer
The correct answer is \(50\) pupils went to W5.
Question 5
\(\frac{3}{4}+\frac{1}{8}=\)?
Answer
You have to convert the first fraction to \(\frac{6}{8}\) before adding the two numerators to get \(\frac{7}{8}\).
Question 6
\(\frac{3}{5}-\frac{1}{9}=\)?
Answer
Fractions should have the same denominator before you can subtract.
So \(\frac{27}{45}-\frac{5}{45}=\frac{22}{45}\).
Question 7
Write the answer to the following in its simplest form: \(\frac{5}{6}\times\frac{2}{3}=\)
Answer
You have to multiply the two numerators and both denominators, then simplify: \({5}\times{2}={10}\), \({6}\times{3}={18}\), \(\frac{10}{18}=\frac{5}{9}\).
Question 8
Write the answer to the following as a mixed number: \(\frac{7}{10}\div\frac{1}{4}=\)
Answer
Remember to multiply \(\frac{7}{10}\) by \(\frac{4}{1}\) to get \(\frac{28}{10}\).
Then, you need to convert the improper fraction into a mixed number: \(\frac{28}{10}=2\frac{8}{10}=2\frac{4}{5}\).
More on Fractions
Find out more by working through a topic
- count3 of 8

- count5 of 8
- count6 of 8