Problem 4 - Ways and means
Problem 4 is all about using different types of Mathematical averages to find some mystery numbers.
Maths teacher Chris Smith and pupils from Grange Academy are here to explain.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
CHRIS In this challenge, we’re going to use different mathematical averages to find some mystery numbers!
There are three parts to this question. Listen carefully and get a pencil and paper to write down all these numbers.
Part A.
The mean is the total of a set of numbers divided by how many numbers there are.
The average, or mean, of four numbers is 5.
When two more numbers are added, the mean climbs to 6.
If one of those extra numbers is 7, what is the other?
Part B.
A set of three whole numbers has mean 9.
A second set of four whole numbers has mean 16.
A third set of five numbers has mean 25.
If the three sets of numbers are put together, what is the new mean?
Part C.
The median is the middle value in an ordered list of numbers.
Find two sets of five numbers where the median of the first is the mean of the second, and the mean of the first is the median of the second.
And it’s all about different averages, right? And trying to work out mystery numbers.
PUPILS
Remind yourself of those definitions of the means and the median.
Take the challenges one at a time - don’t get them mixed up.
CHRIS Was that the one? No, that was the one you just did. What was the one you did six times six.
PUPIL Try to find the totals that the sets of numbers add up to.
CHRIS How do we find out what the total is? What did you do with four and five? Multiplied to get 20.
PUPILS
It might help to think about how much more or less numbers are from the mean.
Good luck!
Part A

The average (meanThe mean is the total of the numbers divided by how many numbers there are.) of four numbers is 5.
When two more numbers are included, the mean climbs to 6.
If one of those extra numbers is 7, what is the other?

Part B

We're looking at three sets of whole numbers with different means.
- A set of three numbers has mean 9
- A set of four numbers has mean 16
- A set of five numbers has mean 25
If the three sets of numbers are put together, what is its mean?

Part C

Find two sets of five numbers so that:
- the mean of the first set is the medianThe middle value in the sorted set of data. of the second
- the mean of the second is the median of the first

Need a hint?
- Remind yourself of the definitions of the mean and the median.
- There are three parts to this problem. Take the challenges one at a time. Don’t get them all mixed up.
- Try to find the totals that the sets of numbers add up to.
- It might help to think about how much more or less numbers are from the mean.
Solution
Worked out the answer? Here's how you can do it.
This puzzle was all about using mathematical averages to find some mystery numbers.
Part A
We know that the mean of the first four numbers is five.
We don’t know any of the numbers but we don’t need to.
We have enough information to work out that the sum of these four numbers is four times five, which equals twenty.
When two more numbers are included the mean climbs to six.
So the total becomes six times six, which equals thirty six.
If one of those extra numbers is seven what’s the other?
We could take the first sum of numbers away from our new total sum of numbers to work out the sum of the two extra numbers.
Thirty six take away twenty equals sixteen and so the two new numbers must add up to sixteen.
If one of the numbers is seven, we can take that away from the total of sixteen and we find that the number must be nine.
Part B
In this part of the question there were three sets of numbers.
A set of three numbers with a mean of nine, a set of four numbers with a mean of sixteen and a set of five numbers with a mean of twenty five.
The total of all the numbers is three times nine, which is twenty seven, four times sixteen, which is sixty four and five times twenty five, which is one hundred and twenty five.
And the total of all these is two hundred and sixteen.
There are twelve numbers altogether.
So the mean is two hundred and sixteen divided by twelve, which equals eighteen.
Part C
In the last part of the question there were two sets of five numbers.
The mean of each set was the median of the other and there were loads of possibilities.
We’re looking at whole numbers and there are five numbers in each set.
So the total for each set must be divisible by five.
All you have to do then is decide your median number.
Multiply it by five and that will give you the total for the other set of numbers.
So if we choose five as the median of one set, five times five equals twenty five will be the total of the numbers in the other set.
We have to find five numbers that have a total of twenty five.
We could go for one, three, six, seven and eight.
The median of this set is six and so the total of the other set must be thirty.
We’ve already decided that the median in this set is five.
Thirty take away five is twenty five.
So the remaining four numbers must add up to twenty five.
And because five is the median number we need to find two numbers less than five and two numbers greater than five that add up to twenty five.
So that could be two, four, eight and eleven.
There are lots of other sets that this would work for.
See how many you can find.
Part A - Answer

We know that the meanThe mean is the total of the numbers divided by how many numbers there are. of the first four numbers is five.
We have enough information to work out that the sum of these four numbers is:
4 x 5 = 20
When two more numbers are included the mean climbs to six. So the total becomes:
6 x 6 = 36
We could take the first sum of numbers (20) away from our new total sum of numbers (36) to work out the sum of the two extra numbers.
36 - 20 = 16
So the two new numbers must add up to sixteen.


If one of the numbers is seven, we can take that away from the total of sixteen to find the other number:
16 - 7 = 9
The missing number is nine.

Part B - Answer
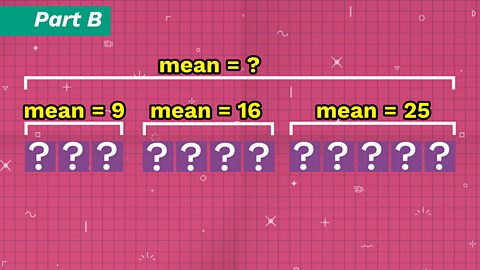
In this part of the question there were three sets of numbers.
- A set of three numbers has mean 9
- A set of four numbers has mean 16
- A set of five numbers has mean 25

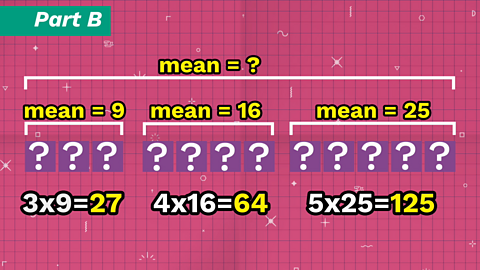
The total of all the numbers is:
3 x 9 = 274 x 16 = 645 x 25 - 125
We can add all these totals together:
27 + 64 + 125 = 216
The total of all these numbers is 216.


There are twelve numbers altogether so the mean is:
216 ÷ 12 = 18
The answer is 18.

Part C - Answer

In the last part of the question there were two sets of five numbers. The mean of each set was the median of the other and there were loads of possibilities.
We’re looking at whole numbers and there are five numbers in each set.
So the total for each set must be divisible by five.


All you have to do then is:
- Choose your median number for the first set of numbers
- Multiply it by five
- This will give you the total for the other set of numbers
There are lots of possibilities for this answer but let's look at one example.


Image caption, Let's choose 5 as the median of one set. 5 x 5 = 25. That means 25 will be the total of the numbers in the other set.

Image caption, We have to find five numbers that have a total of 25. We could go for one, three, six, seven and eight. The median of this set is 6. So the total of the other set must be 30.
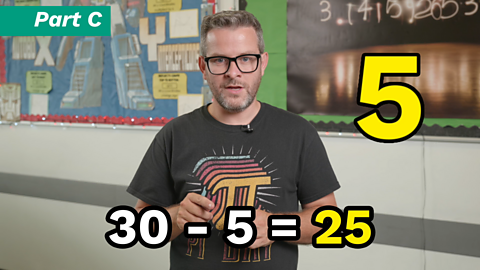
Image caption, We’ve already decided that the median in this set is 5. 30 - 5 = 25. So the remaining four numbers must add up to 25.

Image caption, Because 5 is the median number, we need to find two numbers less than 5 and two numbers greater than 5 that add up to 25. So that could be 2, 4, 8 and 11.
1 of 4
There are lots of other sets that this would work for.
How many can you find?
These are the possibilities for when Set 1 has a mean of 5 and a median of 6, and Set 2 has a mean of 6 and a median of 5.
Set 1
- 1, 2, 6, 7, 9
- 1, 3, 6, 7, 8
- 1, 4, 6, 7, 8
Set 2
- 1,2,5,6,16
- 1,2,5,7,15
- 1,2,5,8,14
- 1,2,5,9,13
- 1,2,5,10,12
- 1,3,5,6,15
- 1,3,5,7,14
- 1,3,5,8,13
- 1,3,5,9,12
- 1,3,5,10,11
- 1,4,5,6,14
- 1,4,5,7,13
- 1,4,5,8,12
- 1,4,5,9,11
- 2,4,5,6,13
- 2,4,5,7,12
- 2,4,5,8,11
- 2,4,5,9,10
- 3,4,5,6,12
- 3,4,5,7,11
- 3,4,5,8,10
There are lots of other pairs of sets of numbers. The key thing is that the total of each set is divisible by five.
Maths Week Scotland 2022. listMaths Week Scotland 2022
Try out all the daily challenges from Maths Week Scotland 2022.

Maths Week Scotland 2021. listMaths Week Scotland 2021
Want more maths challenges? Here are all the problems from 2021.

More on Problem solving
Find out more by working through a topic
- count12 of 21

- count13 of 21

- count14 of 21
- count15 of 21
