Problem 7 - Missing lines
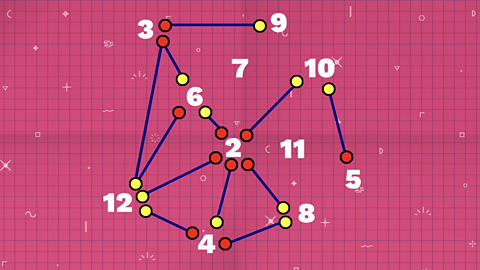
Problem 7 is about a diagram made up of lines, red dots, yellow dots and numbers. There are three lines missing and we need to figure out what's going on.
Maths teacher Chris Smith and pupils from Grange Academy are here to explain.
The Maths Week Scotland Daily Challenges have been set by the Scottish Mathematical Council.
CHRIS For this challenge, we’ve been given a weird diagram with straight lines, red dots, yellow dots and numbers. And we’ve got to figure out what’s going on.
There are three lines missing from this diagram. Where should they go and which ends of each line should have a yellow dot and which a red dot?
Explain your answer.
Your task is to work out where the three missing lines should go in this diagram.
PUPILS Have a go at drawing this out.
Think about the relationships between the numbers that are connected by lines. Are there any patterns?
Why are some dots red and some dots yellow?
Is there a relationship between three and nine or three and six?
What about four? What about its relationship with 2, 8 and 12?
Remember, every number might not be connected by a line.
Give it a go!
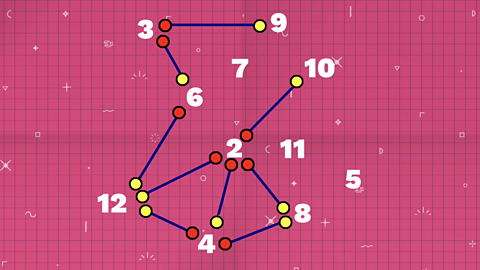
So here's the challenge:
There are three lines missing from this diagram.
Where should the missing lines go? Which ends of each line should have a yellow dot and which a red dot?
Explain your answer.

Need a hint?
- For this challenge, try and think about the relationship between the numbers that are connected by lines.
- Are there any patterns? For example, is there a relationship between 3 and 9 or 3 and 6?
- What about 4? What is its relationship with 2, 8 or 12? And what order are the coloured dots at either side of the line?
- Remember, every number might not be connected by a line.
- You might want to have a go at drawing this out yourself.
Solution
Worked out the answer? Here's how you can do it.
In this challenge we were given a diagram with lines and dots and we had to find the three missing lines.
We are looking for patterns between the numbers that were connected with dots and lines.
Let’s take a look at the number three.
The numbers six and nine can both be divided exactly by three.
Notice that these two lines have red dots next to the three and yellow dots next to the six and nine.
The number six is also connected to the number twelve.
Twelve can be divided exactly by six. So this fits the pattern.
Twelve is also connected to two and four.
Yellow dots at the twelve. Red dots at the two and four.
If we look at the other connected numbers we can see they fit the same pattern.
Eight can be divided by two and four exactly, four can be divided by two exactly, and ten can also be divided by two exactly.
The pattern that we’ve found is that a line leaving a number from a red dot points to a different number into which it divides exactly – marked with a yellow dot.
The first number is a factor of the second.
A factor is a number which divides exactly into another number.
And the second number is a multiple of the first number.
So it can be divided exactly by the smaller one.
The key to solving this weird picture was to figure out that multiples were important and factors were important and those dictated where the lines went.
And the red dots and the yellow dots were clues as to which ones were factors and which ones were multiples.
So to find the three missing lines we’re looking for factors and multiples to join.
Starting with the smallest number, two is a factor of six so we can join those and three is a factor of twelve.
And the final connection joins five and ten.
The numbers seven and eleven, don’t have any dots or lines.
Seven and eleven are prime numbers so they don’t have any factors except for themselves and one.
How did you get on?
Did you work it out?
In this challenge we were given a diagram with lines and dots and we had to find the three missing lines.
We are looking for patterns between the numbers that were connected with dots and lines.
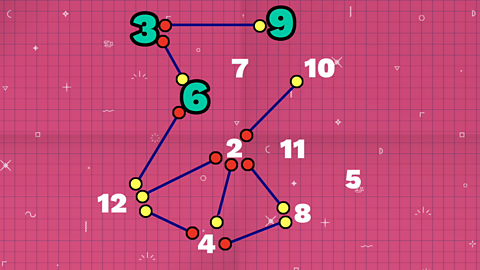
Let’s take a look at the number 3.
The numbers 6 and 9 can both be divided exactly by 3.
Notice that these two lines have red dots next to the three and yellow dots next to the 6 and 9.
The number 6 is also connected to the number 12.
12 can be divided exactly by 6 so this fits the same pattern.

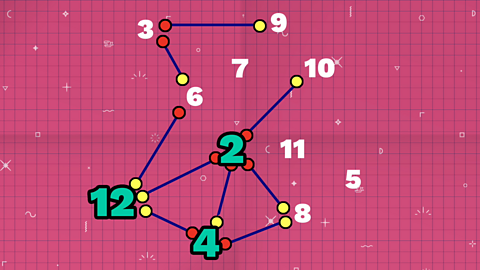
The number 12
12 is also connected to 2 and 4.
Yellow dots at the 12. Red dots at the 2 and 4.
12 can divided exactly by 2 and 4.

If we look at the other connected numbers we can see they fit the same pattern.
- 8 can be divided by 2 and 4 exactly
- 4 can be divided by 2 exactly
- 10 can also be divided by 2 exactly
The pattern that we’ve found is that a line leaving a number from a red dot points to a different number into which it divides exactly – marked with a yellow dot.
- The first number is a of the second.
- The second number is a of the first number so it can be divided exactly by the smaller number.
The missing lines
- 2 is a factor of 6 so we can join those
- 3 is a factor of 12 so we can join those
- 5 is a factor of 10 so we can join those

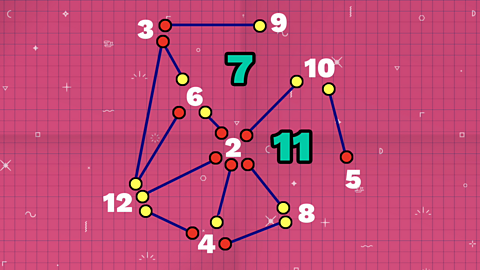
Prime numbers
The numbers 7 and 11 don’t have any dots or lines.
They are prime numbers so they don’t have any factors except for themselves and one.

Maths Week Scotland 2022. listMaths Week Scotland 2022
Try out all the daily challenges from Maths Week Scotland 2022.

Maths Week Scotland 2021. listMaths Week Scotland 2021
Want more maths challenges? Here are all the problems from 2021.

More on Problem solving
Find out more by working through a topic
- count15 of 21

- count16 of 21

- count17 of 21
- count18 of 21