Percentage Change

What is percentage change?

In everyday life, quantities are often changed by a percentage of the original amount.

Percentage Increase/Decrease

In a sale, prices might be decreased by a certain percentage or electricity might have to be increased by a percentage of the present cost.

This is referred to as percentage decrease and percentage increase respectively.

A set of towels normally costs £45.

What will the set cost after the price is reduced in the sale?

\(£45\) is reduced by \(15\%\)

\(15\%~of~45\) = \({45}\times{15}\div{100}\)

\(= £6.75\)

The price has been reduced by \(£6.75\)

The new price is \(£45 - £6.75 = £38.25\)

OR

\(£45\) is reduced by \(15\%\)

The full price is taken to be \(100\%\)

\(100\% - 15\% = 85\%\)

The sale price is \(85\%\) of the full price.

\(85\%~of~45 =\)

\({45}\times{85}\div{100}\)

\(= £38.25\)

The new price is \(£38.25\)

How much cereal will be in the Wheaties packet after the extra is added?

Calculating Percentage Change

Percentage change is the amount that a quantity has changed, expressed as a percentage of the original value.

This can be either an increase or a decrease.

Percentage change can be calculated using the appropriate formula:

\(\%\) increase = \(\frac{(actual~increase)}{(original~value)}\times{100}\)

\(\%\) decrease = \(\frac{(actual~decrease)}{(original~value)}\times{100}\)

Example

A laptop that normally costs \(£550\) is reduced to \(£484\) in a sale.

What is the \(\%\) reduction in the price?

Use the formula:

\(\%\) decrease = \(\frac{(actual~decrease)}{(original~value)}\times{100}\)

Actual decrease \(= £550 – £484 = £66\)

% decrease =\(\frac{66}{550}\times{100} = 12\%\)

Key point

Percentage increase/decrease is always a % of the original quantity.

Question

A family’s gas bill for one year was \(£654\).

The gas company increases the price and the next year their bill is \(£709.59\).

What was the % increase?

To play this video you need to enable JavaScript in your browser.

This video can not be played

A short video showing how to work out percentage increase.

How to work out percentage increase slideshow

Skip image gallery

Image caption,
Click to see a step-by-step slideshow.
Image caption,
WHAT YOU NEED: whiteboard, marker pen, calculator and ruler.
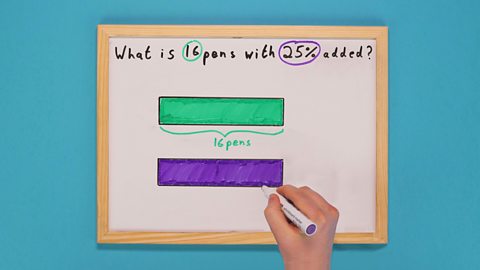
Image caption,
STEP 1: Write out the problem and circle the key pieces of information. Draw a bar, labelling the original amount - in this case 16. Shade the bar in. Draw another bar directly underneath. Shade and label it 100%.
Image caption,
STEP 2: Roughly estimate what the extra 25% would look like and add this area onto the end of the bottom bar. Label this extra area 25% and label 125% at the end of the bar.
Image caption,
STEP 3: Add the same area onto the end of the top bar and label the whole bar with a question mark. Convert each percentage to a decimal. On the bottom bar change the 100% label to 1, change the 125% label to 1.25 and change the 25% label to 0.25.
Image caption,
STEP 4: Multiply the original amount by the decimal to find the new amount. Here it's 16 multiplied by 1.25. Before you use a calculator, can you estimate the answer in your head?
Image caption,
Use a calculator to check your answer.
Image caption,
You’ve done it! Now you know that when you add 25% to 16 you get 20.

To play this video you need to enable JavaScript in your browser.

This video can not be played

A one-minute video showing how to work out a percentage decrease.

How to work out percentage decrease

Skip image gallery

Image caption,
Click to see a step-by-step slideshow.
Image caption,
WHAT YOU NEED: whiteboard, marker pen, calculator and ruler.
Image caption,
STEP 1: Draw a bar and label it with the total amount - in this case £20. Roughly estimate where 75% would be and draw a vertical line. Shade the larger area in and label this with a question mark. Draw a bar directly underneath.
Image caption,
STEP 2: Label 100% at the end of the bar and draw a vertical line directly below the vertical line above. Label the section at the end of the bar 25%. Shade the larger area and label 75% above the vertical line.
Image caption,
STEP 3: Convert each percentage to a decimal by dividing it by 100. On the bottom bar change the 100% label to 1, change the 25% label to 0.25 and change the 75% label to 0.75.
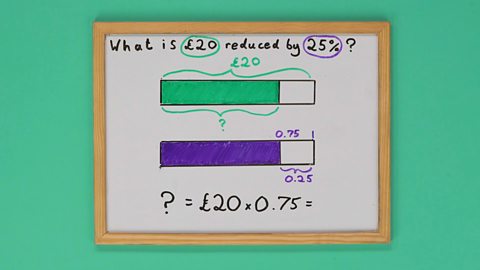
Image caption,
STEP 4: Multiply the original amount by the decimal to find the amount after the decrease. Here it's £20 multiplied by 0.75. Before using a calculator, can you estimate what the answer might be in your head?
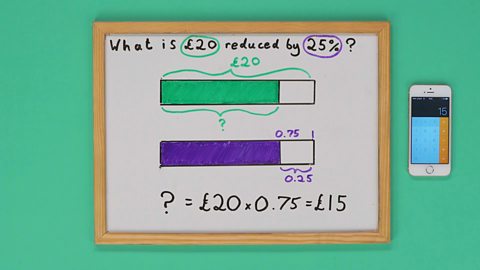
Image caption,
Now use a calculator to check your answer. £20 reduced by 25% is £15.
Image caption,
You’ve done it! Can you visualise this in context? How much would 30% off the marked price be?

Reverse Percentages (finding original value before percentage change)

Naydia spends \(£52\) on a pair of trainers in the sale.

What would they have cost before the sale?

Let the original price = \(100\%\)

The reduction is \(20\%\) so sale price = \(80\%\) of the original.

The trainers cost \(£65\) before the sale.

Question

A car salesperson sold \(378\) cars in 2019.

This was an increase of \(8\%\) on the year before.

How many cars did she sell in 2018?

To play this video you need to enable JavaScript in your browser.

This video can not be played

A one-minute video showing how to work out the original value before a percentage change.

Work out original value slideshow

Skip image gallery

Image caption,
Click to see a step-by-step guide.
Image caption,
WHAT YOU NEED: whiteboard, ruler, pens and a calculator.
Image caption,
STEP 1: Draw a bar: if the whole bar was 100%, estimate where 40% from the right would be and draw a vertical line. Label the left-hand part £12 and shade it in. Now label the whole bar with a question mark. Draw a bar underneath and label it 100%.
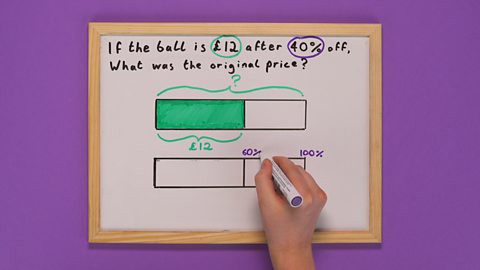
Image caption,
STEP 2: On the bottom bar draw a vertical line directly underneath the vertical line on the top bar. Label it 60%, representing the price after a 40% discount, then shade the area in. Label the right-hand segment 40%, which represents the discount.
Image caption,
STEP 3: Convert the percentages to decimals by dividing them by 100. So on the bottom bar replace the 60% label with 0.60, the 100% label with 1 and the 40% label with 0.40.
Image caption,
STEP 4: The bars show that the original amount x 0.60 = £12. This means that £12 ÷ 0.60 = the original amount. Before you use a calculator, can you estimate what the answer might be in your head?
Image caption,
Use a calculator to check your answer. You’ve done it! Now you know that the original price of the football was £20.

Repeated Percentage Change

Repeated Percentage Change is when an amount changes a number of times by a given %.

Example

Amy buys a nearly new car costing \(£10500\).

The dealer tells her that the value of the car will depreciate (decrease) by \(8\%\) each year.

How much will the car be worth after 3 years?

Decrease in first year:

\(8\%\) of \(£10500\) = \(£840\).

Value at the end of first year = \(£10500 - 840 = £9660\)

Decrease in second year:

\(8\%\) of \(£9660 = £772.80\).

Value at the end of second year \(= £9660 - £772.80 = £8887.20\)

Decrease in third year:

\(8\%\) of \(£8887.20 = £71.10\) (nearest penny)

Value at the end of third year \(= £8887.20 - £710.98 = £8176.22\)

Amy’s car will be worth \(£8176.22\) after 3 years

Alternative method

There is an alternative and much quicker method.

The value of the car decreases by \(8\%\) each year.

This is \(92\%\) of the value for the previous year.

\(92\% = 0.92\)

After one year the value will be:

\({10500}\times{0.92}\)

After two years the value will be:

\({10500}\times{0.92}\times{0.92}\)

After three years the value will be:

\({10500}\times{0.92}\times{0.92}\times{0.92} = {10500}\times{0.92}^3\)

\({10500}\times{0.92}^3 = {£8176.22}\) (nearest penny)

Question

The population of a town is \(42000\).

Planners estimate that it will increase by \(0.7\%\) every year.

Calculate the estimated population in two years’ time.

Test section

Question 1

A calculator normally costs \(£18\) but the price is reduced by \(12\%\) in a promotion.

What is the reduced price?

Question 2

The population of a town increases from \(67500\) to \(72600\).

What is the percentage increase?

Question 3

Zak runs a \(10k\) race in \(40\) minutes.

The next week he runs it in \(38\) minutes.

What is the percentage reduction in his time?

Question 4

After a reduction of \(15\%\), a sofa is priced at \(£680\).

What was the price before the reduction?

Question 5

Daisy’s annual salary has been increased by \(4\%\) to \(£26000\).

What was her salary before the increase?

Question 6

In 2020, it was estimated that house prices in Northern Ireland were increasing by \(2.4\%\) every year.

In January 2020, the average house price \(£143000\).

What will the average house price be in January 2022?

Give your answer to the nearest \(£\).

Where next?

Discover more maths topics on Bitesize.

Maths

What is percentage change?

Percentage Increase/Decrease

OR

OR

Calculating Percentage Change

Example

Key point

Question

Answer

How to work out percentage increase slideshow

How to work out percentage decrease

Reverse Percentages (finding original value before percentage change)

Question

Answer

Work out original value slideshow

Repeated Percentage Change

Example

Alternative method

Question

Answer

Test section

Question 1

Answer

Question 2

Answer

Question 3

Answer

Question 4

Answer

Question 5

Answer

Question 6

Answer

Where next?

More on Percentages

What is percentage change?

Percentage Increase/Decrease

OR

Show answerHide answer

OR

Calculating Percentage Change

Example

Key point

Question

Show answerHide answer

Answer

How to work out percentage increase slideshow

How to work out percentage decrease

Reverse Percentages (finding original value before percentage change)

Question

Show moreShow less

Answer

Work out original value slideshow

Repeated Percentage Change

Example

Alternative method

Question

Show answerHide answer

Answer

Test section

Question 1

Show answerHide answer

Answer

Question 2

Show answerHide answer

Answer

Question 3

Show answerHide answer

Answer

Question 4

Show answerHide answer

Answer

Question 5

Show answerHide answer

Answer

Question 6

Show answerHide answer

Answer

Where next?

More on Percentages